K-means真的不能使用曼哈顿距离吗？

问题

说到k-means聚类算法，想必大家已经对它很熟悉了，它是基于距离计算的经典无监督算法，但是有一次在我接受面试时，面试官问了我一个问题：“k-means为什么不能使用曼哈顿距离计算，而使用欧式距离进行计算？”，当时我顿时懵了，心想：‘难道不都可以吗？’，我只能说都可以，然后面试官给了我一个眼神，“你回去查查吧，看看到底为什么”,然后我就回家啦。这是我后来在网上找到的回答，如下图：

k-means基本思想：

1.在样本数据中随机设置n个聚类中心（X_i,Y_i），假设数据只有二维；

2.计算样本数据距离聚类中心（X_i,Y_i）距离D_i，并各自归属到距离自己最近的中心点；

3.各个汇聚到一起的簇计算各自的平均值，将新的平均值作为新的中心点；

4.然后重复2、3两步，直到中心点的移动范围小于阈值或达到循环最大次数。

距离公式

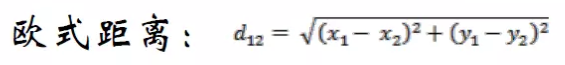
欧式距离也叫欧几里得距离，也是最广泛使用的距离计算公式，指n维空间中两点间的直线距离

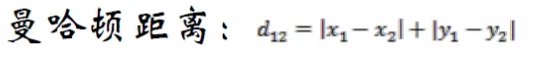
曼哈顿距离指同一坐标系下两点差的绝对值之和

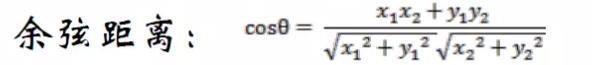
多说一个，余弦距离指空间中原点与两点连线所夹角度的大小

分析

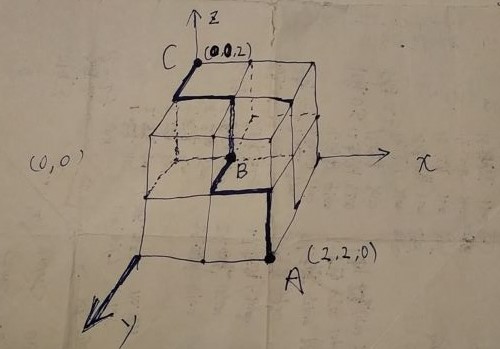
那到底k-means、knn能不能用曼哈顿计算呢，如第一张图片所示，这是别人的答案，表示曼哈顿具有维度限制，真的是这样吗，我认为并不是这样的，大家都知道曼哈顿距离可以计算二维空间两点距离，那么尝试在三维空间进行计算，由此可以推广到高维空间，如下手画图所示：

一个2x2x2的立方体，坐落在三维坐标轴上，点A（2，2，0），点C（0，0，2），求AC的曼哈顿距离，根据曼哈顿公式计算得：

|0-2|+|0-2|+|2-0|=6，显而易见，实际距离也是6，路线有很多条，但结果都是一样的。

结论

综上所述，曼哈顿距离适合k-means，只是各种距离算法可能需要在不同业务场景或数据下选择使用。