Blind Estimation and Detection of Space-Time Trellis Coded Transmissions over the Rayleigh Fading MIMO Channel

目录

• 文章来源
• 摘要
• 基本概念
  • 粒子滤波
  • 时间序列模型
• 系统模型
  • 通信系统
  • 经典状态空间表示
  • 论文所提出的状态空间表示
• 借鉴之处

文章来源

IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 56, NO. 3, MARCH 2008，Frederic Lehmann

摘要

　　该论文对STTC（space-time trellis codes）下的未知平坦信道进行盲估计，在接收端使用粒子滤波算法。其结果与已知完美信道条件下使用VA（Viterbi Algorithm）性能接近。

基本概念

粒子滤波

　　在一个时间离散动态系统中，用下面的方程来表示：

　　其中，第一个等式是过程等式：从上一个过程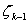转移到当前过程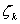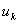，是在有限序列中取。第二个等式是状态等式。第三个等式是测量等式。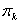和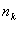分别是过程噪声和测量误差。
　　在使用粒子滤波估计时，算法框图如下：

时间序列模型

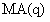　　是移动平均过程，表示如下：

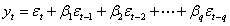
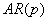　　是自回归过程，表示如下：

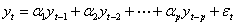
系统模型

通信系统

　　该论文使用STTC编码，并将其通过BPSK映射。在第j个天线上接受到的观测值为：

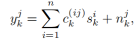
　　其中是在第k个时间间隙，从第i个发送天线到第j个接受天线的复时变信道增益.

经典状态空间表示


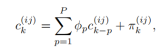
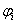　　是独立于衰落率的非零常数。对于上式可以改写为如下：


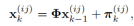
　　定义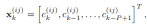其中
　

　　为了看的清楚期间，将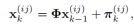具体化开，如下：
　

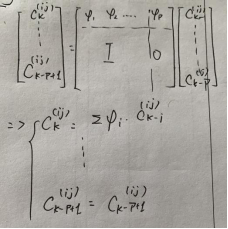
　　再将不同的收发天线聚合在一个矩阵里，

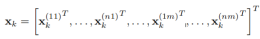
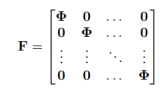
　　在原始发送的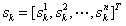每个发送符号中间插入P-1个0：

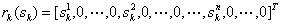
　　而在接收端所观察到的矩阵如下：

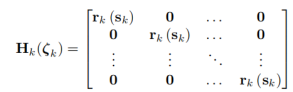
论文所提出的状态空间表示

　　论文将瑞丽衰落信道参数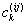使用指数级数表示（感觉像是傅里叶变换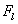），是独立于衰落率的确定参数：

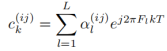
　　第j个接受天线对应的信道叠加系数：

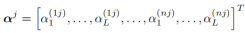
　　然后根据这个信道叠加系数将原来的变成如下的形式：

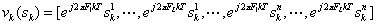
　　就是将序列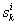中的每一个扩展成一个L长的序列。
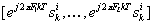　　而最初的信道函数就变成：

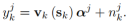
　　同样的，将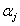扩展成

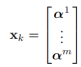
　　这样就可以把之前的空间状态描述改成：


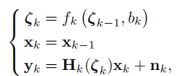
借鉴之处

　　1.从每个时隙每个收发天线上的信息聚合为整个系统的某一时隙的转移矩阵，然后在时间维度上聚合，变成整个系统的时变转移矩阵。
　　2.将信道转移参数使用矩阵表示，构造一个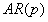，将后一个转移参数用前P个转移参数加权表示。
　　3.在考虑时变信道时，在频域将某一个时隙的信号扩展成一个频带内的信号。即在某一个频段内都发送该信号，更能准确的确定时变信道在信号传递频段内的变化情况。