题解 SP2916 【GSS5 - Can you answer these queries V】

前言

最近沉迷于数据结构，感觉数据结构很有意思。

正文

分析

先来分类讨论一下

1. \(x2<y1\)

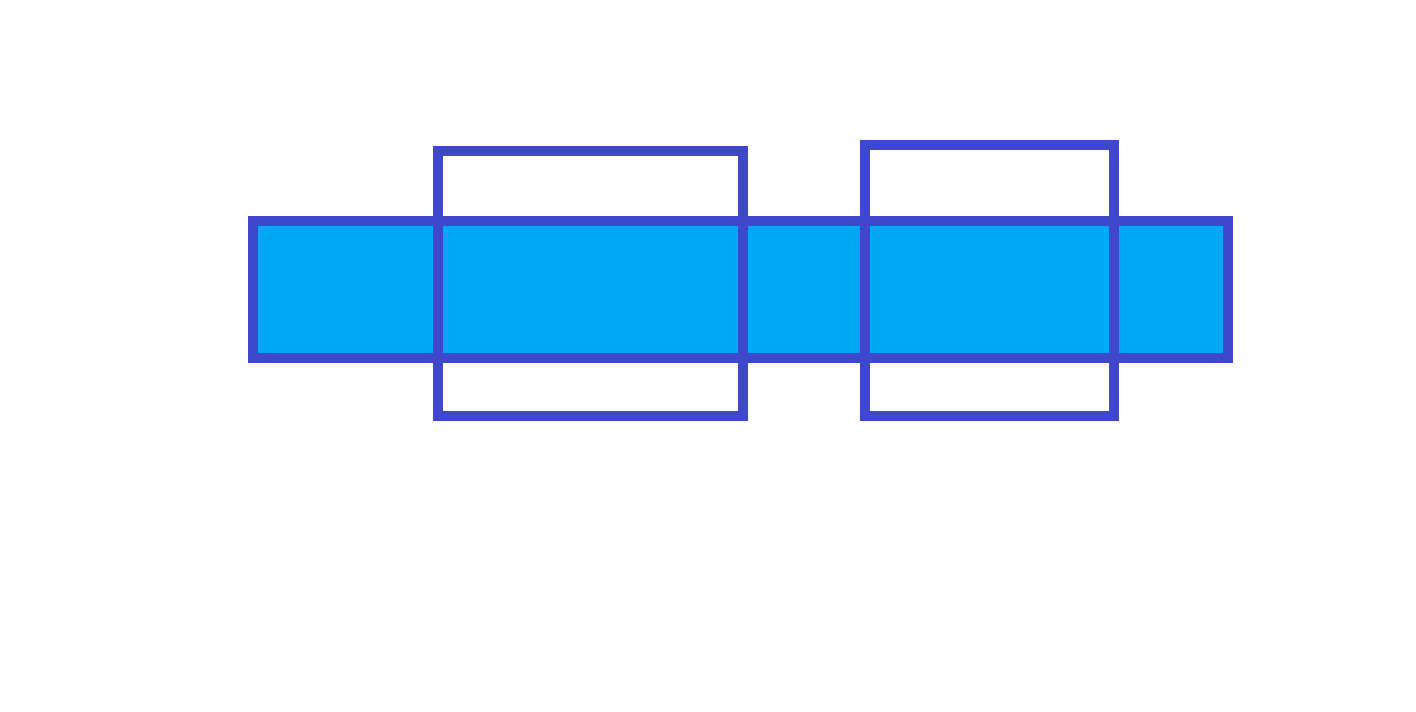
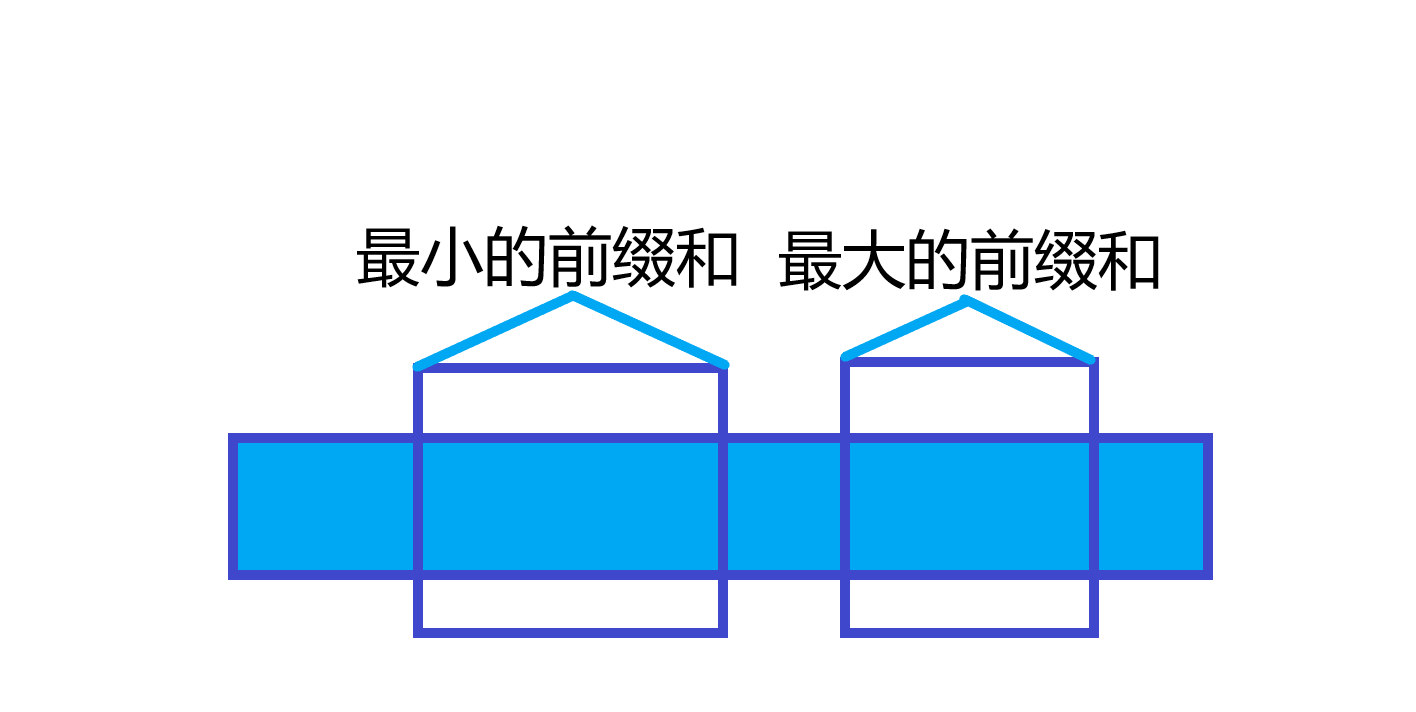
如果 \(y1<x2\) 的话，答案 \(=\max \limits_{ y1 \leq x \leq y2} \{ s_i \} - \min \limits_{x1 \leq x \leq x2} \{ s_i \}\)

其中 \(s_i\) 表示 \(\sum\limits_{j=1}^{i} a_j\) ，就是俗称的前缀和

这个东西可以用线段树维护。

2. \(x2>=y1\)

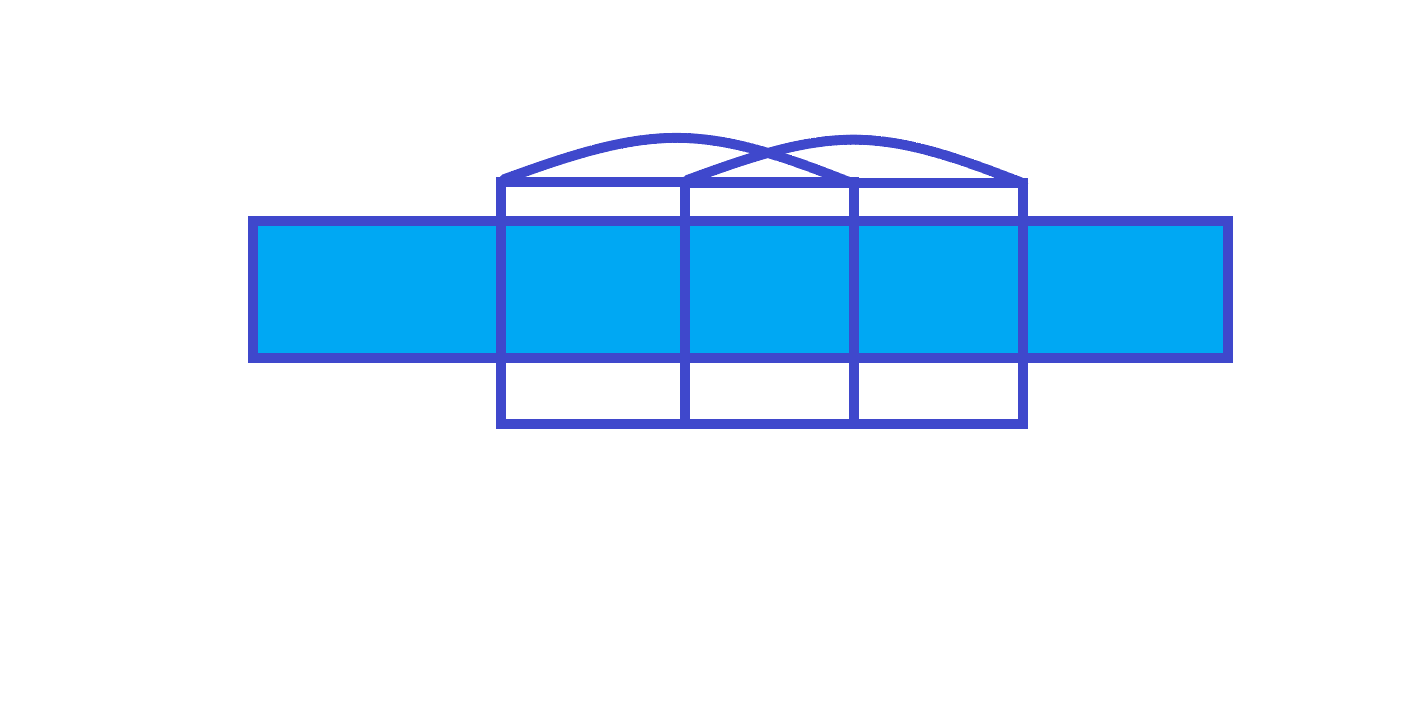
这个怎么处理呢

答案 \(=\) \(\max \begin{cases}\max \limits_{ y1 \leq x \leq y2} \{ s_i \} - \min \limits_{x1 \leq x \leq y1} \{ s_i \}\\ \max \limits_{ x2 \leq x \leq y2} \{ s_i \} - \min \limits_{x1 \leq x \leq x2} \{ s_i \}\\ f(x,y)\end{cases}\)

这里的 \(f\) 函数就是最大子段和。

不会用线段树求最大子段和的可以看这里

最上面的 \(2\) 个也是可以用线段树来维护的。

代码

最后要注意的一点是前缀和，我们知道区间 \([i,j]\) 的和 $ = s_j-s_{i-1}$，而不是 $ = s_j-s_{i}$

这个怎么处理呢，我们发现我们的题目全部都是用 \(Max\) 函数的答案减去 \(Min\) 函数的答案，所以，我们可以把线段树维护的 \(\min\) 全部减去 \(a_{i}\)

现在这份代码就能 \(A\) 了

#include <bits/stdc++.h>
#define ls num<<1
#define rs num<<1|1
using namespace std;
typedef long long ll;
template<typename T>inline void read(T &FF){
	T RR=1;FF=0;char CH=getchar();
	for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
	for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
	FF*=RR;
}
template<typename T>void write(T x){
	if(x<0)putchar('-'),x*=-1;
	if(x>9)write(x/10);
	putchar(x%10+48);
}
template<typename T>void writen(T x){
	write(x);
	puts("");
}
const int MAXN=5e4+10;
struct Tree{
	int l,r;
	ll lans,rans,sum,ans,max,min;
}t[MAXN*4];
int a[MAXN],x,y,n,T,T_,l1,r1,l2,r2;
ll s[MAXN];
Tree pushup(Tree L,Tree R){
	Tree z;
	z.sum=L.sum+R.sum;
	z.lans=max(L.lans,L.sum+R.lans);
	z.rans=max(R.rans,R.sum+L.rans);
	z.ans=max(max(L.ans,R.ans),L.rans+R.lans);
	z.max=max(L.max,R.max);
	z.min=min(L.min,R.min);
	z.l=L.l;z.r=R.r;
	return z;
}
void build(int l,int r,int num){
	if(l==r){
		t[num].l=l;
		t[num].r=r;
		t[num].sum=a[l];
		t[num].lans=a[l];
		t[num].rans=a[l];
		t[num].ans=a[l];
		t[num].max=s[l];
		t[num].min=s[l]-a[l];
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid,ls);
	build(mid+1,r,rs);
	t[num]=pushup(t[ls],t[rs]);
}
Tree query(int num){
	if(x<=t[num].l&&t[num].r<=y)return t[num];
	if(t[rs].l>y)return query(ls);
	if(t[ls].r<x)return query(rs);
	return pushup(query(ls),query(rs));
}
ll Max(int num){
	if(t[num].l>=x&&t[num].r<=y)return t[num].max;
	if(t[ls].r<x)return Max(rs);
	if(t[rs].l>y)return Max(ls);
	return max(Max(ls),Max(rs));
}
ll Min(int num){
	if(t[num].l>=x&&t[num].r<=y)return t[num].min;
	if(t[ls].r<x)return Min(rs);
	if(t[rs].l>y)return Min(ls);
	return min(Min(ls),Min(rs));
}
ll Mx(int a,int b){
	x=a;y=b;
	return Max(1);
}
ll Mn(int a,int b){
	x=a;y=b;
	return Min(1);
}
ll qy(int a,int b){
	x=a;y=b;
	return query(1).ans;
}
int main(){
	read(T);
	while(T--){
		read(n);
		for(int i=1;i<=n;i++)read(a[i]);
		for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i];
		build(1,n,1);
		read(T_);
		while(T_--){
			read(l1);read(r1);read(l2);read(r2);
			if(r1>l2)writen(max(qy(l2,r1),max(Mx(l2,r2)-Mn(l1,l2),Mx(r1,r2)-Mn(l1,r1))));
			else writen(Mx(l2,r2)-Mn(l1,r1));
		}
	}
	return 0;
}

后记

这篇题解如果有问题可以私信或评论，告诉我，一起完善