Manthan, Codefest 19

Contest Info
Solutions

Contest Info

Solved	A	B	C	D	E	F	G	H
6/8	O	O	Ø	O	O	Ø	-	-

O 在比赛中通过
Ø 赛后通过
! 尝试了但是失败了
- 没有尝试

Solutions

A. XORinacci

题意：
$f(0) = 1, f(1) = b, f(n) = f(n - 1) \oplus f(n - 2)$，求$f(n)$。

思路：
循环节为$3$。

B. Uniqueness

题意：
给出一个序列$a_i$，可以删去连续的一段，使得剩下的数是互不相同的。
求删除的那一段的最小长度。

思路：
枚举左端点，那么一个右端点可行，当且仅当左端点左边的数是互不相同的，右端点右边的数是互不相同的，并且右端点右边的数中没有左端点左边的数。

左端点左边的数是互不相同的，右端点右边的数是互不相同的
- 这两个条件可以$O(n)$预处理。
右端点右边的数中没有左端点左边的数。
- 这个条件可以维护左端点的数中最后一次出现的位置的最大值，那么右端点比这个最大值还大即可。

C. Magic Grid

题意：
构造一个$n \cdot n$的矩阵，里面的数为$[0, n^2 - 1]$的一个排列。
要求每一行以及每一列的异或和相同。
$n = 4k$.

思路：
对于$4$的情况这样构造：

0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

发现每一行每一列都是$0$。
那么对于$n = 4k$的情况，直接划分成若干个$4 \cdot 4$的小矩形，这样仿照的画葫芦即可。

D. Restore Permutation

题意：
有一个排列$p_i$，现在告诉你$s_i$：
\[
\begin{eqnarray*}
s_i = \sum\limits_{p_j < p_i} p_j
\end{eqnarray*}
\]
要求还原出$p_i$。

思路：
显然一个合法的$s_i$的序列唯一对应一个$p_i$序列，那么我们从最后一个数考虑。
假设最后一个数为$p_n$，那么$s_n = p_n(p_n - 1) / 2$。
其实本质就是小于$p_n$的数都在它前面，他们的和构成了$s_n$。
那么确定了最后一个数，那么依次倒着确定$s_{n - 1}, s_{n - 2}, \cdots$。
用线段树维护还有哪些数没有出现，以及他们的和。
对于每个$s_i$，在线段树上二分即可。

E. Let Them Slide

题意：
有一个$n \cdot w$的矩形，每一行有若干个数，并且每一行的数是可以整体移动的，像这样：

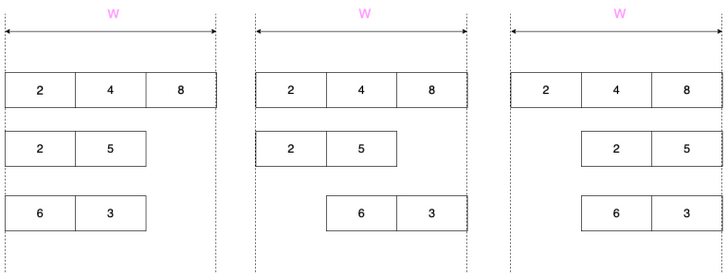
那么现在询问，对于每一列，下面每一行的数如何移动，使得该列的数的和最大，如果没有数那么就是$0$。
每一列的询问独立。

思路：
每一行考虑，考虑这一行的哪些数会对哪些列产生贡献。
显然这个每个数产生贡献的范围是连续的，那么用栈贪心维护一下范围即可。

F. Bits And Pieces

题意：
给出一个序列$a_i$，询问$a_i \;|\; (a_j \& a_k)$这个式子的最大值，其中$i < j < k$

思路：
考虑固定$a_i$，然后我们只需要关心$a_i$那些二进制位上为$0$的位，从高位到低位确定。
比如说对于第$x$位，那么我们相当于固定了一个前缀，去找$i < j < k$是否存在一个$a_j$以及一个$a_k$，它们都有这样的前缀。
那么直接枚举子集标记前缀即可。但是这样复杂度不对。
我们可以倒着来，因为我们发现对于一个$(j, k)$，那么肯定希望$j, k$越大越好，那么倒着标记即可，这样标记过了肯定不用再标记了，因为被标记过说明下标肯定大于等于当前的下标。
但是要注意下标等于的情况