ROC与AUC的定义与使用详解

分类模型评估：

指标	描述	Scikit-learn函数
Precision	精准度	from sklearn.metrics import precision_score
Recall	召回率	from sklearn.metrics import recall_score
F1	F1值	from sklearn.metrics import f1_score
Confusion Matrix	混淆矩阵	from sklearn.metrics import confusion_matrix
ROC	ROC曲线	from sklearn.metrics import roc
AUC	ROC曲线下的面积	from sklearn.metrics import auc

回归模型评估：

指标	描述	Scikit-learn函数
Mean Square Error (MSE, RMSE)	平均方差	from sklearn.metrics import mean_squared_error
Absolute Error (MAE, RAE)	绝对误差	from sklearn.metrics import mean_absolute_error, median_absolute_error
R-Squared	R平方值	from sklearn.metrics import r2_score

ROC和AUC定义

ROC全称是“受试者工作特征”（Receiver Operating Characteristic）。ROC曲线的面积就是AUC（Area Under the Curve）。AUC用于衡量“二分类问题”机器学习算法性能（泛化能力）。

计算ROC需要知道的关键概念

首先，解释几个二分类问题中常用的概念：True Positive, False Positive, True Negative, False Negative。它们是根据真实类别与预测类别的组合来区分的。

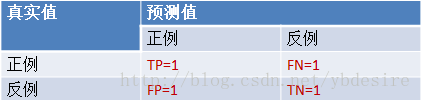
假设有一批test样本，这些样本只有两种类别：正例和反例。机器学习算法预测类别如下图（左半部分预测类别为正例，右半部分预测类别为反例），而样本中真实的正例类别在上半部分，下半部分为真实的反例。

• 预测值为正例，记为P（Positive）
• 预测值为反例，记为N（Negative）
• 预测值与真实值相同，记为T（True）
• 预测值与真实值相反，记为F（False）

• 

• TP：预测类别是P（正例），真实类别也是P

• FP：预测类别是P，真实类别是N（反例）
• TN：预测类别是N，真实类别也是N
• FN：预测类别是N，真实类别是P

样本中的真实正例类别总数即TP+FN。TPR即True Positive Rate，TPR = TP/(TP+FN)。 
同理，样本中的真实反例类别总数为FP+TN。FPR即False Positive Rate，FPR=FP/(TN+FP)。

还有一个概念叫”截断点”。机器学习算法对test样本进行预测后，可以输出各test样本对某个类别的相似度概率。比如t1是P类别的概率为0.3，一般我们认为概率低于0.5，t1就属于类别N。这里的0.5，就是”截断点”。 
总结一下，对于计算ROC，最重要的三个概念就是TPR, FPR, 截断点。

截断点取不同的值，TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线，就是ROC曲线。横轴用FPR表示。

sklearn计算ROC

sklearn给出了一个计算ROC的例子[1]。

1.  
   y = np.array([1, 1, 2, 2])
2.  
   scores = np.array([0.1, 0.4, 0.35, 0.8])
3.  
   fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)

• 1
• 2
• 3

• 1
• 2
• 3

通过计算，得到的结果（TPR, FPR, 截断点）为

1.  
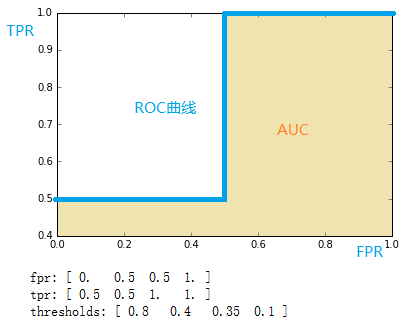
   fpr = array([ 0. , 0.5, 0.5, 1. ])
2.  
   tpr = array([ 0.5, 0.5, 1. , 1. ])
3.  
   thresholds = array([ 0.8 , 0.4 , 0.35, 0.1 ])#截断点

• 1
• 2
• 3

• 1
• 2
• 3

将结果中的FPR与TPR画到二维坐标中，得到的ROC曲线如下（蓝色线条表示），ROC曲线的面积用AUC表示（淡黄色阴影部分）。

详细计算过程

上例给出的数据如下

1.  
   y = np.array([1, 1, 2, 2])
2.  
   scores = np.array([0.1, 0.4, 0.35, 0.8])

• 1
• 2

• 1
• 2

用这个数据，计算TPR，FPR的过程是怎么样的呢？

1. 分析数据

y是一个一维数组（样本的真实分类）。数组值表示类别（一共有两类，1和2）。我们假设y中的1表示反例，2表示正例。即将y重写为：

y_true = [0, 0, 1, 1]

 

• 1

• 1

score即各个样本属于正例的概率。

2. 针对score，将数据排序

样本	预测属于P的概率(score)	真实类别
y[0]	0.1	N
y[2]	0.35	P
y[1]	0.4	N
y[3]	0.8	P

3. 将截断点依次取为score值

将截断点依次取值为0.1,0.35,0.4,0.8时，计算TPR和FPR的结果。

3.1 截断点为0.1

说明只要score>=0.1，它的预测类别就是正例。 
此时，因为4个样本的score都大于等于0.1，所以，所有样本的预测类别都为P。

1.  
   scores = [0.1, 0.4, 0.35, 0.8]
2.  
   y_true = [0, 0, 1, 1]
3.  
   y_pred = [1, 1, 1, 1]

• 1
• 2
• 3

• 1
• 2
• 3

TPR = TP/(TP+FN) = 1 
FPR = FP/(TN+FP) = 1

3.2 截断点为0.35

说明只要score>=0.35，它的预测类别就是P。 
此时，因为4个样本的score有3个大于等于0.35。所以，所有样本的预测类有3个为P（2个预测正确，1一个预测错误）；1个样本被预测为N（预测正确）。

1.  
   scores = [0.1, 0.4, 0.35, 0.8]
2.  
   y_true = [0, 0, 1, 1]
3.  
   y_pred = [0, 1, 1, 1]

• 1
• 2
• 3

• 1
• 2
• 3

TPR = TP/(TP+FN) = 1 
FPR = FP/(TN+FP) = 0.5

3.3 截断点为0.4

说明只要score>=0.4，它的预测类别就是P。 
此时，因为4个样本的score有2个大于等于0.4。所以，所有样本的预测类有2个为P（1个预测正确，1一个预测错误）；2个样本被预测为N（1个预测正确，1一个预测错误）。

1.  
   scores = [0.1, 0.4, 0.35, 0.8]
2.  
   y_true = [0, 0, 1, 1]
3.  
   y_pred = [0, 1, 0, 1]

• 1
• 2
• 3

• 1
• 2
• 3

TPR = TP/(TP+FN) = 0.5 
FPR = FP/(TN+FP) = 0.5

3.4 截断点为0.8

说明只要score>=0.8，它的预测类别就是P。所以，所有样本的预测类有1个为P（1个预测正确）；3个样本被预测为N（2个预测正确，1一个预测错误）。

1.  
   scores = [0.1, 0.4, 0.35, 0.8]
2.  
   y_true = [0, 0, 1, 1]
3.  
   y_pred = [0, 0, 0, 1]

• 1
• 2
• 3

• 1
• 2
• 3

TPR = TP/(TP+FN) = 0.5 
FPR = FP/(TN+FP) = 0

心得

用下面描述表示TPR和FPR的计算过程，更容易记住

• TPR：真实的正例中，被预测正确的比例
• FPR：真实的反例中，被预测正确的比例

最理想的分类器，就是对样本分类完全正确，即FP=0，FN=0。所以理想分类器TPR=1，FPR=0。

参考：

1. http://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html
2. ROC计算公式，http://blog.yhat.com/posts/roc-curves.html
3. 《机器学习》，周志华