MySQL B+树的插入与删除

一、MySQL Index 的插入

有如下B+树，其高度为2，每页可存放4条记录，扇出为5。所有记录都在叶子节点上，

并且是顺序存放，如果用户从最左边的叶子节点开始顺序遍历，可以得到所有简直的顺序

排序:5、10、15、20、25、30、50、55、60、65、75、80、85、90。

B+树的插入操作，分为三种情况

1、Leaf Page和Index Page都没满

用户插入28这个值，Leaf Page和Index Page都没满，直接插入即可

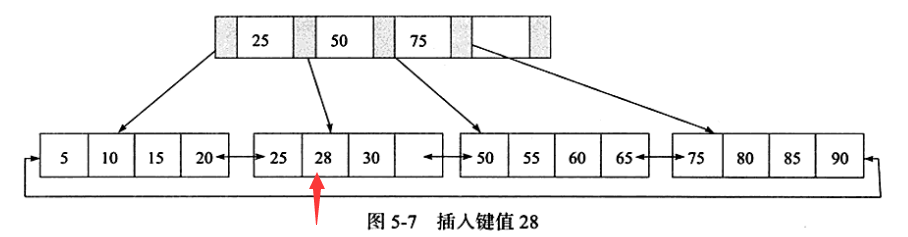
2、Leaf Page已经满了，Index Page没有满

用户插入70这个值，Leaf Page已经满了，Index Page没有满。

这是插入Leaf Page后情况为50、55、60、65、70，并根据中间值60来拆分叶节点。

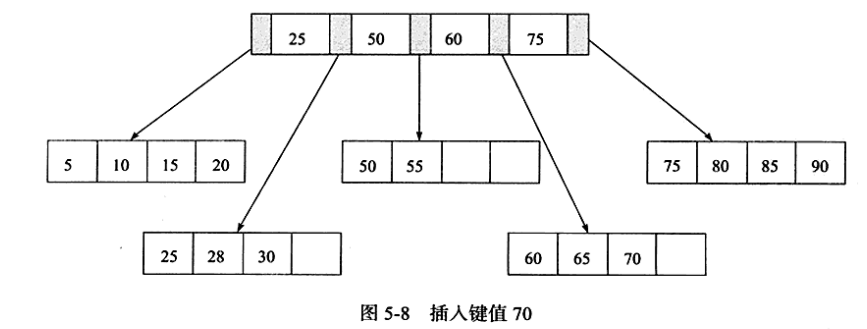
3、Leaf Page和Index Page都满了

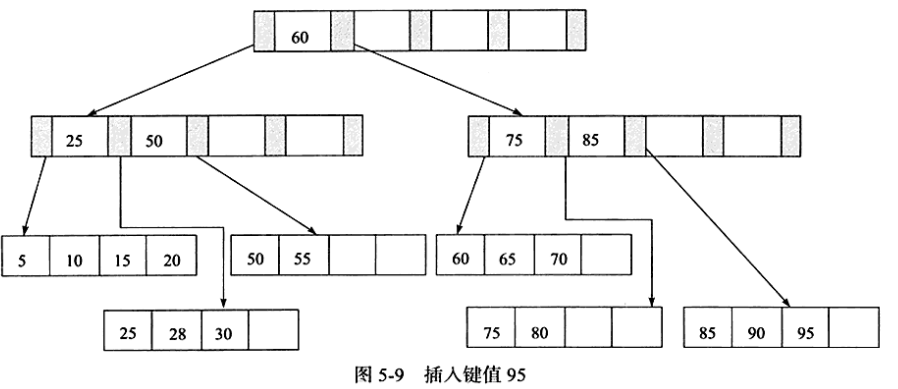
插入95这个值，Leaf Page和Index Page都满了，这是需要两次拆分

1）首先插入Leaf Page后情况为75、80、85、90、95，由于Leaf Page已经满了，需要根据中间值85拆分叶节点，小于85的放左边即75、80；

大于等于85的放右边即85、90、95。

2）将中间节点85放入Index Page后，Index Page的值为25、50、60、75、85，由于Index Page也满了，需要拆分Index Page，取中间值60，

放入上层Index Page中，小于60的25、50放在左边；大于60的值75、85放在右边。

4、B+树的旋转（继承平衡二叉树的旋转功能）

不管怎么变化B+树总是保持平衡。但是为了保持平衡杜宇先插入的键值可能需要做大量的拆分操作。因为B+树结构主要用于磁盘，页的拆分意味着磁盘操作，所以应该在可能的情况下尽量减少页的拆分操作。因此，B+树同样提供了类似平衡二叉树的旋转（Rotation）功能。

旋转发生在Leaf Page已满，其左右兄弟没满的情况下。B+树不急于做拆分，通常情况下左兄弟会被首先检查用来做旋转操作。

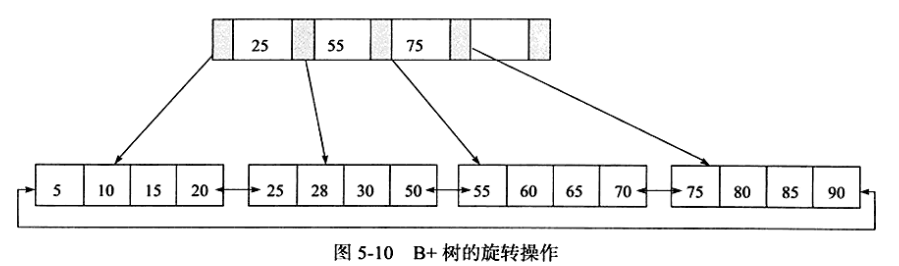
插入键值70，其实B+树并不会急于去拆分叶子节点，而是去做旋转操作，得到如图

采用旋转操作使得B+树减少了一次页的拆分操作，同时B+树的高度依然是2。

二、MySQL Index 的删除

B+树使用填充因子（fill factor）来控制树的删除变化，50%是填充因子可以设置的最小值。B+树的删除操作同样必须保证删除后叶子节点中的记录依然排序，同插入一样，B+树的删除操作同样有三种情况，与插入不同的是，删除时根据填充因子的变化衡量。

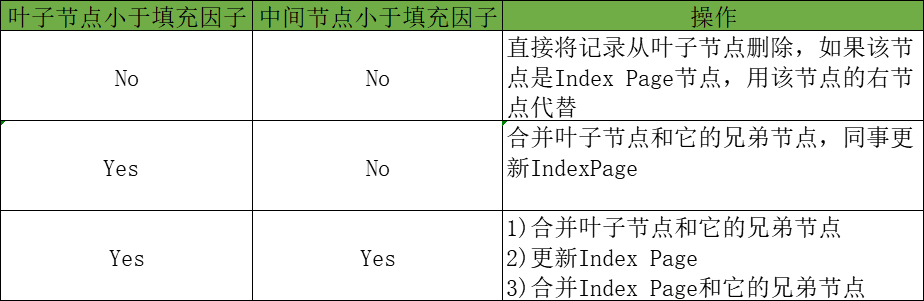
1、叶子节点大于填充因子、中间节点大于填充因子

1）删除键值为70的这条记录，该记录符合第一种情况，删除后可得下图

2）接着5-11，再删除键值为25的记录，这也是讨论的第一种情况，但是该值是Index Page中的值，因此在删除Leaf Page中的25后，还应该将25的兄弟节点的28更新到Page Index中。

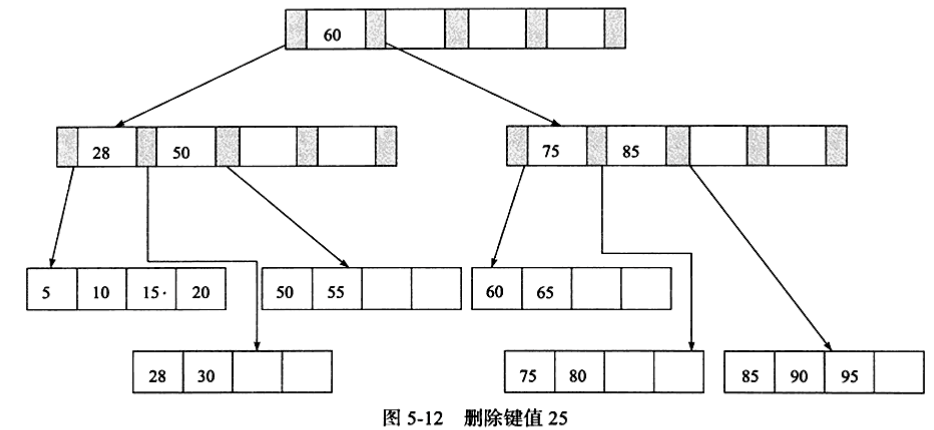
2、叶子节点小于填充因子、中间节点大于填充因子

3、叶子节点小于填充因子、中间节点小于填充因子

最后删除键值60的情况。删除Leaf Page中键值为60的记录后，Fill Factor小于50%，这时需要做合并操作，同样，再删除Index Page中相关记录后，需要做Index Page的合并操作，最后如图

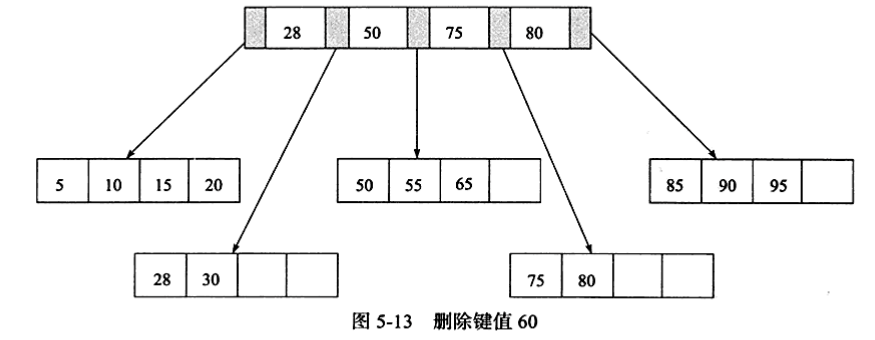
三、一些概念

1、索引扇出

扇出：是指该模块直接调用的下级模块的个数。扇出大表示模块的复杂度高，需要控制和协调过多的下级模块；但扇出过小（例如总是1）也不好。
扇出过大一般是因为缺乏中间层次，应该适当增加中间层次的模块。扇出太小时可以把下级模块进一步分解成若干个子功能模块，或者合并到它的上级模块中去。

2、索引填充因子

和索引重建最相关的是填充因子。当创建一个新索引，或重建一个存在的索引时，你可以指定一个填充因子，它是在索引创建时索引里的数据页被填充的数量。填充因子设置为100意味着每个索引页100％填满，50％意味着每个索引页50％填满。
如果你创建一个填充因子为100的聚集索引（在一个非单调递增的列上），那意味着每当一个记录被插入（或修改）时，页拆分都会发生，因为在现存的页上没有这些数据的空间。