1205: 求一元二次方程的实数根（C）

一、题目

acm.wust.edu.cn/problem.php?id=1205&soj=0

二、分析

1. 一元二次方程有三个系数a、b、c，两个根x1、x2，以及d（德尔塔）；
2. a、b、c均为实数，以及输出保留6位小数，全部定义为double类型；
3. a、b、c均为0，退出并结束；
4. 方程有两个根，从大到小输出，中间一个空格；
5. 两根相同输出一个即可；
6. 无解输出-1；
7. 多组输入。

三、思路

计算d（德尔塔）：

1. d=0，x1=-b/(2*a)，输出x1；
2. d>0，x1=(-b+sqrt(d))/(2*a)，x2=(-b-sqrt(d))/(2*a)，用fmax，fmin函数，依次输出较大数，较小数；
3. 否则，输出-1。

四、代码

#include<stdio.h>
#include<math.h>
int main() {
	double a, b, c, d, x1, x2; // 三个系数，德尔塔，两个根
	while (scanf("%lf%lf%lf", &a, &b, &c) != EOF) {
                // 三个系数均为0，退出
		if (a == 0 && b == 0 && c == 0) {
			break;
		}
		d = b * b - 4 * a*c; // 计算德尔塔
		if (d == 0) { // 一个根
			x1 = -b / (2 * a);
			printf("%lf\n", x1);
		}
		else if (d > 0) { // 两个根
			x1 = (-b + sqrt(d)) / (2 * a);
			x2 = (-b - sqrt(d)) / (2 * a);
			// 先输出较大的，再输出较小的
			printf("%lf %lf\n", fmax(x1, x2), fmin(x1, x2));
		}
		else { // 无解
			printf("%d\n", -1);
		}
	}
	return 0;
}

五、截图

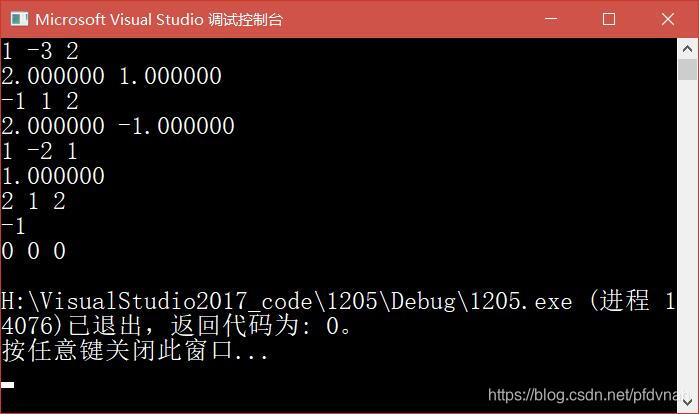
备注：注意第二组数据。