Dfs【bzoj3252】攻略

Description

题目简述：树版[k取方格数]

众所周知，桂木桂马是攻略之神，开启攻略之神模式后，他可以同时攻略k部游戏。

今天他得到了一款新游戏《XX半岛》，这款游戏有n个场景(scene)，某些场景可以通过不同的选择支到达其他场景。所有场景和选择支构成树状结构：开始游戏时在根节点（共通线），叶子节点为结局。每个场景有一个价值，现在桂马开启攻略之神模式，同时攻略k次该游戏，问他观赏到的场景的价值和最大是多少（同一场景观看多次是不能重复得到价值的）

“为什么你还没玩就知道每个场景的价值呢？”

“我已经看到结局了。”

Input

第一行两个正整数n,k

第二行n个正整数，表示每个场景的价值

以下n-1行,每行2个整数a,b，表示a场景有个选择支通向b场景（即a是b的父亲）

保证场景1为根节点

n<=200000，1<=场景价值<=2^31-1

Output

输出一个整数表示答案

如果我们的图是这样

显然,这样我们会选择\(8\),而不会选择\(6,5\)。

此时我们按照价值划分为长短链,当前的父亲节点\(u\)就带有价值\(8\)，这个时候直接塞过去就好.

此时就可以等价为我们拆成了这样

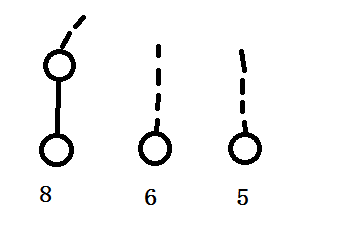
此时,我们的答案就转化为求这些链的权值的前\(k\)大的和.

代码

#include<cstdio>
#include<cctype>
#include<algorithm>
#define int long long
#define R register
using namespace std;
inline void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,k,val[200008],stk[200008],cnt,top,ans;
int head[200008],tot,son[200008];
struct cod{int u,v;}edge[500008];
inline void add(int x,int y)
{
	edge[++tot].u=head[x];
	edge[tot].v=y;
	head[x]=tot;
}
void dfs(int u,int fa)
{
	for(R int i=head[u];i;i=edge[i].u)
	{
		if(edge[i].v==fa)continue;
		dfs(edge[i].v,u);
		if(val[edge[i].v]>val[son[u]])
			son[u]=edge[i].v;
	}
	val[u]+=val[son[u]];
	for(R int i=head[u];i;i=edge[i].u)
	{
		if(edge[i].v==fa or edge[i].v==son[u])continue;
		if(val[edge[i].v]>val[u])
			swap(val[edge[i].v],val[u]);
		stk[++top]=val[edge[i].v];
	}
}
signed main()
{
	in(n),in(k);
	for(R int i=1;i<=n;i++)in(val[i]);
	for(R int i=1,x,y;i<n;i++)
	{
		in(x),in(y);
		add(x,y);add(y,x);
	}
	dfs(1,0);
	stk[++top]=val[1];
	sort(stk+1,stk+top+1);
	for(R int i=top;i>=0;i--)
	{
		cnt++;
		ans+=stk[i];
		if(cnt==k)break;
	}
	printf("%lld",ans);
}