Python进行数值计算

1.计算积分

（1）计算定积分

from scipy import integrate

#定义函数
def half_circle(x):

　　 return (1-x**2)**0.5

pi_half, err = integrate.quad(half_circle, -1, 1)

print(pi_half*2)  #err为误差精度

(2)计算二重积分

def half_sphere(x, y):
return (1-x**2-y**2)**0.5

print(integrate.dblquad(half_sphere, -1, 1,lambda x:-half_circle(x),lambda x:half_circle(x))[0])

2.计算常微分方程

(1)案例一，计算洛仑兹吸引子的轨迹

# -*- coding: utf-8 -*-
from scipy.integrate import odeint
import numpy as np 

def lorenz(w, t, p, r, b):
    # 给出位置矢量w，和三个参数p, r, b计算出
    # dx/dt, dy/dt, dz/dt的值
    x, y, z = w
    # 直接与lorenz的计算公式对应
    return np.array([p*(y-x), x*(r-z)-y, x*y-b*z]) 

t = np.arange(0, 30, 0.01) # 创建时间点
# 调用ode对lorenz进行求解, 用两个不同的初始值
track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0))
track2 = odeint(lorenz, (0.0, 1.01, 0.0), t, args=(10.0, 28.0, 3.0)) 

# 绘图
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt 

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2])
ax.plot(track2[:,0], track2[:,1], track2[:,2])
plt.show()

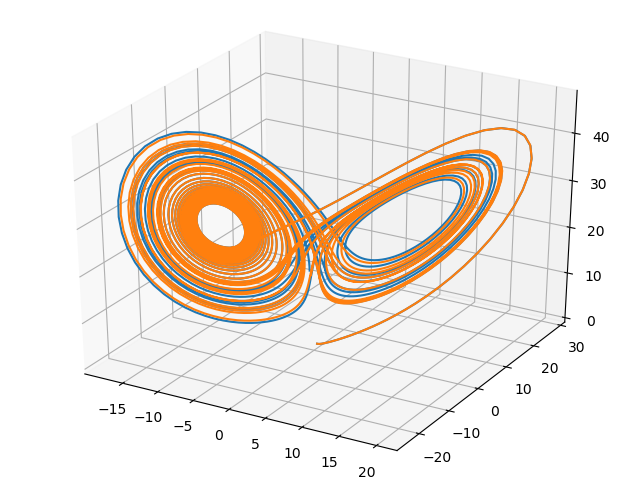
（2）案例二

#y"+a*y'+b*y=0
from scipy.integrate import odeint
from pylab import *
def deriv(y,t): # 返回值是y和y的导数组成的数组
　　a = -2.0
　　b = -0.1
　　return array([ y[1], a*y[0]+b*y[1] ])
time = linspace(0.0,50.0,1000)
yinit = array([0.0005,0.2]) # 初值
y = odeint(deriv,yinit,time)

figure()
plot(time,y[:,0],label='y') #y[:,0]即返回值的第一列，是y的值。label是为了显示legend用的。
plot(time,y[:,1],label="y'") #y[:,1]即返回值的第二列，是y’的值
xlabel('t')
ylabel('y')
legend()
show()