Catalan数计算及应用

Catalan数列是非常奇妙的一列数字，因为很多问题的解就是一个Catalan数。知道了这一规律，很多看似复杂的问题便可迎刃而解。那么什么是Catalan数，什么样的问题的解是Catalan数呢？

1，Catalan数

先来看一段Catalan数列：1,1,2,5,14,42,132,429,1430,4862,16796，即 h(0)=1,h(1)=1,h(2)=2,h(3)=5...

怎么求出来的呢？两种方式

(1) h(n)=h(0)*h(n-1)+h(1)*h(n-2)+...+h(n-1)*h(0). 这是一个递归的公式。

(2) h(n)=c(n2,n)/(n+1). 由这个公式可以直接求出h(n)，不需要知道h(n-1)...h(0).

在直接想要知道h(n)的时候，公式（2）很好用，但是在解决一些算法问题的时候，第一个公式更有用些，因为这一类算法全都能搞成公式（1）的样子求解。

2，Catalan数的应用

(1) n对括号有多少种匹配方式？

比如一对括号肯定有一种匹配方式(),两对括号呢，两种()()和(())，n对呢？

可以用分治的思想来。假设第一个(可以和i个)匹配了，即(...)...这个样子，那么整个大问题可以分成两个子问题，这种情况下有多少个配对等于红色点点部分的子问题有的配对数目乘以绿色点点部分的子问题配对数目。所有的匹配数目就等于所有有第一个括号配对的选择而带来的子问题的解的和。即n对括号匹配数目f(n)为，

f(n)=f(0)*f(n-1)+f(1)*f(n-1)+...+f(n-1)*f(0)

怎么理解？

f(0)*f(n-1)就是：()...第一个(与第一个)配对了，产生的两个子问题就是左边的0对括号的匹配和右面n-1对的括号的匹配。

f(1)*f(n-1)就是:(())..第一个(与第二个)配对了，产生的子问题就是左边的1对括号的匹配和右面n-2对括号的匹配。

而这个f(n)的公式是不是就是Catalan的递归公式呢？完全相同，因此n对括号的匹配数就是Catalan数h(n).

(2) 矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

也是分治的思想，先通过一个括号将大问题分成小问题。比如(a1×a2)×(a3×a4×a5×a6...),然后再解决两个小问题的括号化问题。所以n个矩阵相乘的括号方案f(n)可以表达为

f(n)=f(1)*f(n-1)+f(2)*f(n-2)+...+f(n-1)*f(1).

所以f(n)=h(n-1)

(3) 一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

进栈相当于左括号，出栈相当于右括号，这个问题和问题1是等价的。比如，123的进栈出栈序列可以表示为32，红色表示进栈，绿色表示出栈，红色的对应(，绿色对应)。那么这个序列其实就是()(()).

所以这个问题的解还是h(n).

(4)n个节点构成的二叉树，共有多少种情形？

有n个节点，这些节点的值不重要，重要的是如果选择第i个节点作为树的根，那么这棵树的左子树就会有i-1个节点，右子树就会有n-i-1个节点。

所以总共可能的二叉树有

f(n)=f(0)*f(n-1)+f(1)*f(n-2)....+f(n-1)*f(0)

也是Catalan数h(n)

(5)在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？

以其中一个点为基点，编号为0，然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数，否则，这两个编号间含有奇数个点，势必会有个点被孤立，即在一条线段的两侧分别有一个孤立点，从而导致两线段相交。设选中的基点为A，与它连接的点为B，那么A和B将所有点分成两个部分，一部分位于A、B的左边，另一部分位于A、B的右边。然后分别对这两部分求解即可。所以，

f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。

(0)*f(n-2)表示编号0的点与编号1的点相连，此时位于它们右边的点的个数为0，而位于它们左边的点为2n-2。依次类推。

f(0) = 1, f(2) = 1, f(4) = 2。结合递归式，不难发现f(2n) 等于h(n)。

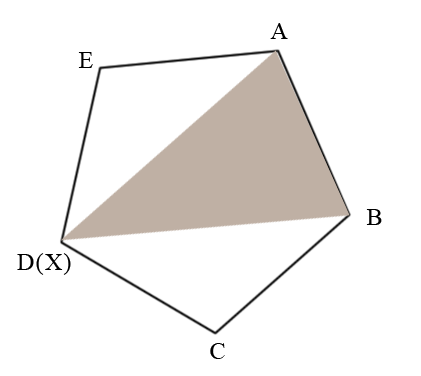
(6)求一个凸多边形区域划分成三角形区域的方法数？

设凸边行为ABCDEF...，以凸多边形的一边为基，设这条边的2个顶点为A和B。从剩余顶点中选1个记为X，可以将凸多边形分成三个部分，中间是一个三角形（ABX），左右两边分别是两个凸多边形（B(BX之间的点)X，AX(从X到A的点)），然后求解左右两个凸多边形。

设问题的解f(n)，其中n表示顶点数，那么f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形，那么另外两个部分的顶点数分别为2和n-1。

设f(2) = 1，那么f(3) = 1, f(4) = 2, f(5) = 5。结合递推式，不难发现f(n) 等于h(n-2)。

(7) 有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？

5元的人来是一个进栈，10元的人来是一个出栈。如果这个问题只考虑进栈和出栈的方式，不考虑具体的人，那么应该有h(n)中安排方式。也可以就考虑这些5元钱，它们总是要都进来一遍，然后又会全出的。

(8)标准二维表问题。设n是一个正整数，2×n的标准二维表是有正整数1,2,...,2n组成的2×n数组，该数组的每行从左到右递增，每列从上到下递增。2×n的标准二维表全体记为Tab(n)。例如当n=3时，Tab(3)二维表如下图所示：

1 2 3　　1 2 4　　1 2 5　　1 3 4　　1 3 5

4 5 6  　 3 5 6　　3 4 6　　2 5 6　　2 4 6

这个问题可以转为为问题(1)。对每个配对的括号从左到右编号，左括号对应的编号放在第一行，右括号对应的编号放在第二行，因为编号从左到右按照顺序，而且右括号的编号肯定比左括号的编号大。比如：()()()对应[1 3 5][2 4 6]这个表，()(())对应[1 3 4][2 5 6]这个表。

因此Tab(n)=h(n).

(9)n个节点的二叉树的不同形态的个数

不同形态的二叉树的数目恰好是前序序列均为1,2,3...n的二叉树所能的到的中序序列的数目。而中序遍历的过程实质上是一个点进栈和出栈的过程。二叉树的形态确定了其节点进栈和出栈的顺序，也确定了其中序序列。因此这个问题就变成问题3.