[BZOJ4538]网络

今天打比赛，毒瘤yww把这题出到$n,m\leq 5\times10^5$，因为不会写整体二分所以来写坑爹的$O\left(n\log_2n\right)$做法

考虑按重要度建权值线段树（相同权值的请求视作不同的），每个线段树节点存这个区间内的链的交集

那么插入删除就直接搞，询问时在线段树上贪心，如果当前节点的右儿子有请求且它的链交集不覆盖询问点，那么往右儿子走，否则往左儿子走

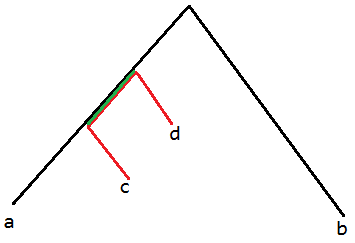
链的交集还是链，我们要求$(a,b)$和$(c,d)$的交集，如果$lca_{a,b}$在$(c,d)$上，那么一定有交集，交集为$(\text{low}({lca_{c,a}},lca_{c,b}),\text{low}(lca_{d,a},lca_{d,b}))$（其中$\text{low}(a,b)$表示$a,b$中的较低点），反过来也是一样的

细节有点多，为了跑得更快，求lca的部分可以转成rmq然后用ST表$O(1)$查询

#include<stdio.h>
#include<map>
using namespace std;
int h[100010],nex[200010],to[200010],fa[100010],dep[100010],fir[100010],dfn[200010],mp[200010][20],log2[200010],M;
void add(int a,int b){
	M++;
	to[M]=b;
	nex[M]=h[a];
	h[a]=M;
}
void dfs(int x){
	M++;
	dfn[M]=x;
	fir[x]=M;
	for(int i=h[x];i;i=nex[i]){
		if(to[i]!=fa[x]){
			dep[to[i]]=dep[x]+1;
			fa[to[i]]=x;
			dfs(to[i]);
			M++;
			dfn[M]=x;
		}
	}
}
int querymin(int l,int r){
	int k=log2[r-l+1];
	if(dep[dfn[mp[l][k]]]<dep[dfn[mp[r-(1<<k)+1][k]]])
		return mp[l][k];
	else
		return mp[r-(1<<k)+1][k];
}
int lca(int x,int y){
	if(fir[x]>fir[y])swap(x,y);
	return dfn[querymin(fir[x],fir[y])];
}
struct ask{
	int op,x,y,v,id;
}q[200010];
bool operator<(ask a,ask b){
	if(a.v==b.v)return a.id<b.id;
	return a.v<b.v;
}
map<ask,int>pos;
map<ask,int>::iterator it;
int s[800010],lp[800010],rp[800010],rv[200010];
int dis(int x,int y){
	return dep[x]+dep[y]-2*dep[lca(x,y)];
}
bool inc(int x,int y,int u){
	return dis(x,u)+dis(u,y)==dis(x,y);
}
void pushup(int x){
	if(s[x<<1]==0||s[x<<1|1]==0){
		lp[x]=lp[x<<1]|lp[x<<1|1];
		rp[x]=rp[x<<1]|rp[x<<1|1];
		return;
	}
	if(lp[x<<1]==0||lp[x<<1|1]==0){
		lp[x]=rp[x]=0;
		return;
	}
	int a,b,c,d,e,f,h,i;
	a=lp[x<<1];
	b=rp[x<<1];
	c=lca(a,b);
	d=lp[x<<1|1];
	e=rp[x<<1|1];
	f=lca(d,e);
	if(inc(a,b,f)){
		h=lca(d,a);
		i=lca(d,b);
		lp[x]=dep[h]>dep[i]?h:i;
		h=lca(e,a);
		i=lca(e,b);
		rp[x]=dep[h]>dep[i]?h:i;
		return;
	}
	if(inc(d,e,c)){
		h=lca(a,d);
		i=lca(a,e);
		lp[x]=dep[h]>dep[i]?h:i;
		h=lca(b,d);
		i=lca(b,e);
		rp[x]=dep[h]>dep[i]?h:i;
		return;
	}
	lp[x]=rp[x]=0;
}
void insert(int p,int L,int R,int l,int r,int x){
	s[x]++;
	if(l==r){
		lp[x]=L;
		rp[x]=R;
		return;
	}
	int mid=(l+r)>>1;
	if(p<=mid)
		insert(p,L,R,l,mid,x<<1);
	else
		insert(p,L,R,mid+1,r,x<<1|1);
	pushup(x);
}
void erase(int p,int l,int r,int x){
	s[x]--;
	if(l==r){
		lp[x]=rp[x]=0;
		return;
	}
	int mid=(l+r)>>1;
	if(p<=mid)
		erase(p,l,mid,x<<1);
	else
		erase(p,mid+1,r,x<<1|1);
	pushup(x);
}
int query(int u,int l,int r,int x){
	if(s[x]==0)return-1;
	if(l==r)return inc(lp[x],rp[x],u)?-1:rv[l];
	int mid=(l+r)>>1;
	if(s[x<<1|1]!=0&&(lp[x<<1|1]==0||!inc(lp[x<<1|1],rp[x<<1|1],u)))
		return query(u,mid+1,r,x<<1|1);
	else
		return query(u,l,mid,x<<1);
}
int main(){
	int n,m,i,j,x,y;
	scanf("%d%d",&n,&m);
	for(i=1;i<n;i++){
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	M=0;
	dfs(1);
	for(i=2;i<=M;i++)log2[i]=log2[i>>1]+1;
	for(i=1;i<=M;i++)mp[i][0]=i;
	for(j=1;j<20;j++){
		for(i=1;i<=M;i++){
			if(i+(1<<j)-1<=M){
				if(dep[dfn[mp[i][j-1]]]<dep[dfn[mp[i+(1<<(j-1))][j-1]]])
					mp[i][j]=mp[i][j-1];
				else
					mp[i][j]=mp[i+(1<<(j-1))][j-1];
			}
		}
	}
	for(i=1;i<=m;i++){
		scanf("%d%d",&q[i].op,&q[i].x);
		if(q[i].op==0){
			scanf("%d%d",&q[i].y,&q[i].v);
			q[i].id=i;
			pos[q[i]]=1;
		}
	}
	M=1;
	for(it=pos.begin();it!=pos.end();it++,M++){
		it->second=M;
		rv[M]=(it->first).v;
	}
	M--;
	for(i=1;i<=m;i++){
		if(q[i].op==0)insert(pos[q[i]],q[i].x,q[i].y,1,M,1);
		if(q[i].op==1)erase(pos[q[q[i].x]],1,M,1);
		if(q[i].op==2)printf("%d\n",query(q[i].x,1,M,1));
	}
}