（原创）BFS广度优先算法，看完这篇就够了

BFS算法

上一篇文章讲解了DFS深度优先遍历的算法，我们说 DFS 顾名思义DEEPTH FIRET，以深度为第一标准来查找，以不撞南墙不回头的态度来发掘每一个点，这个算法思想get到了其实蛮简单。那么 BFS 和DFS有什么相同点和不同点呢？

我觉得有一种比喻对于 DFS 和 BFS 从方法论的角度解释很到位，DFS 就像是小明要在家里找到钥匙，因为对位置的不确定，所以一间一间的来找，深度遍历能确保小明走过所有的屋子。而 BFS 像是近视的小明的眼镜掉在了地上，小明肯定是先摸索离手比较近的位置，然后手慢慢向远方延伸，直至摸到眼镜，像是以小明为中心搜索圈不断扩大的过程。所以如果说 DFS 从遍历的层次结构上类似树的先序遍历，那么BFS算法按照里外顺序逐渐增加深度的做法，就像极了朴素的层次遍历，例如：

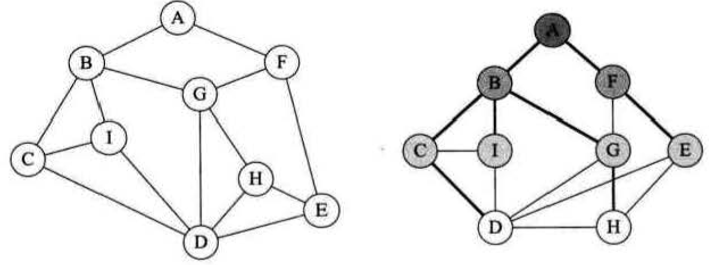
把左图拉平，按照层序把结点排列下来，各节点的连接关系并没有变，图结构没有发生变化，但是这时，我们从A出发，按层序遍历可以得到顺序是 A B F C I G E D H

结合上一篇文章的 DFS ，我们可以发现这两种算法的区别在每一个点上都能得以体现，比如 A 点，DFS 鼓励结点向着一个方向冲，BFS 则会在一个点上按照顶点下标次序遍历完所有没有访问过的结点，比如A点遍历完，马上开始扫描，如果 B F这两个点没有被宠幸过，那么一定要翻完 B、F 这两个点的牌子之后，才会继续访问第二层，即把A点相连的结点全部遍历完成才行，当然到了第二层 发现 B、F 早就被A安排过了，就不再进入这两个点的循环，后面的一样，这里就不再赘述。

我们回忆一下DFS算法，DFS沿着一个方向走最后是要走回头路的，因为它迟早会遍历到一个所有分支都被访问过的结点，那么要走回头路意味着我们实现 DFS 时应该选择后进先出的栈结构，而现在的 BFS 算法是每经过一个点就会遍历所有没访问过的点，同时，一个点如果已经访问完，那么它就没有利用价值了，所以应该使用队列先进先出的特点

这里是图形演示：

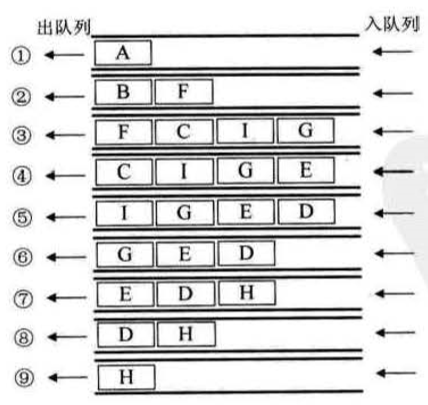
下面我们来看代码实现：

这是邻接矩阵实现 BFS 算法，结构定义见上一篇文章

void BFS(MGraph *G)
{
    int i,j;
    Queue Q;
    InitQueue(&Q);
    for(i = ; i < G.numVertexes;i++)
    {
        visited[i] = FALSE;
    }
    for(i = ;i < G.numVertexes;i++)
    {
        if(!visited[i])
        {
            visited[i] = TRUE;
            printf("%c",&G.vexs[i]);
            EnQueue(&Q,i);
            while(!QueueEmpty(Q))
            {
                DeQueue(&Q,&i);
                for(j = ;j < G.numVertexes;j++)
                {
                    while(G.arc[i][j] ==  && !visited[j])
                    {
                        visited[j] = TRUE;
                        printf("%c",G.vexs[j]);
                        EnQueue(&Q,j);
                    }
                }
            }
        }
    }
}

这是邻接表实现的代码：

void BFS(GraphAdjList GL)
{
    int i;
    Queue Q;
    EdgeNode *p;
    InitQueue (&Q);
    for(i = ;i < GL->shuliang;i++)
    {
        visited[i] = FALSE;
    }
    for(i = ;i < GL->shuliang;i++)
    {
        if(!visited[i])
        {
            visited[i] = TURE;
            printf("%c",GL->adjlist[i].data);
            EnQueue(&Q,i);
            while(!QueueEmpty(Q))
            {
                DeQueue(&Q,&i);
                p = GL->adjlist[i].firstedge;
                while(p)
                {
                    if(!visited[p -> adjvex])
                    {
                        visited[p -> adjvex] = TRUE;
                        printf("%c",GL->adjlist[p -> adjvex].data);
                        EnQueue(&Q,p->adjvex);
                    }
                    p = p -> next;
                }
            }
        }
    }

}

个人感觉代码蛮好懂，这一块感觉需要多多思考，广度优先和深度优先小到日常生活，大到数据模型，有着广泛的作用，而这篇文章中的两种方法，因为都要遍历整张图，所以其算法时间复杂度相同，所以对于全图遍历并没有什么明确选择的优势，而如果目的在于尽快地找到目的点，那么深度优先更占优势；而如果是不断扩大遍历范围，寻找相对最优解则是广度优先看起来更划算。算法就到这里，经验和思路只能靠大家自己在实践中多多总结，得到自己使用的一套方法。