AVL重平衡细节——插入

话说这个系列鸽了好久，之前在准备语言考试，就没管博客了，现在暑假咱们继续上路！

每当我们进行一次插入之后，整棵AVL树的平衡性就有可能发生改变，为了控制整棵树的高度，我们需要通过一系列变换（重平衡）来保证它仍满足AVL的平衡条件。我们把需要重新平衡的节点叫做 ⍺，由于任意节点最多有两个儿子，因此高度不平衡时，⍺的两颗子树高度差2。考虑一下产生不平衡会有几种情况，稍加思索就会明白——四种情况的插入：

1. ⍺->left->left
2. ⍺->left->right
3. ⍺->right->left
4. ⍺->right->right

情形1和4，2和3 分别是关于⍺的镜像对称，从理论上来讲只有两种情况，当然，从编程角度还是四种情况。

先说一些约定：

struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;

struct AvlNode
{
    int value;
    AvlTree  lc;
    AvlTree  rc;
    int      Height;
};

int max(int a,int b){ return a>b?a:b;}

下面先从思路角度予以说明，一段思路说清后立即给出代码实现，趁热打铁，就易于接受了。

外侧情形-单旋转

第一种情况是发生在外侧（左-左or右-右），情形1、4，这需要一次单旋转来完成。

先说“右-右”的情况，这种旋转也叫zag

这里两个灰色的方块是可能插入的节点，虚线连接表示只能取一处，g是可能发生失衡的最深的节点（因为往上的祖先也有可能发生失衡），而g就是当前发生失衡最近的节点。我们要围绕着g做一次”右-右“旋转。先说一下宏观的思路：为了使树恢复平衡，我们把p的右子树整体上移一层，并把T0下移一层，不过这样一来，实际上超出了AVL的特性要求，为此我们重新安排节点以形成一颗等价的树，如下所示：

抽象地形容就是：把树形象地看成是柔软灵活的，抓住节点p，闭上你的双眼使劲摇动它，在重力作用下p就成了新的根。BST的性质告诉我们，在原树中g<p，于是在新树中g变成了

p的左孩子，T0和p的右子树的各自隶属关系仍然不变。子树T1包含原树中介于g和p之间的的那些节点（因为原树中g<T1<p），可以将它放在新树中g的右孩子的位置上，这样所有对元素大小的要求都能得到满足了。

怎么做呢？首先用一个临时指针指向p

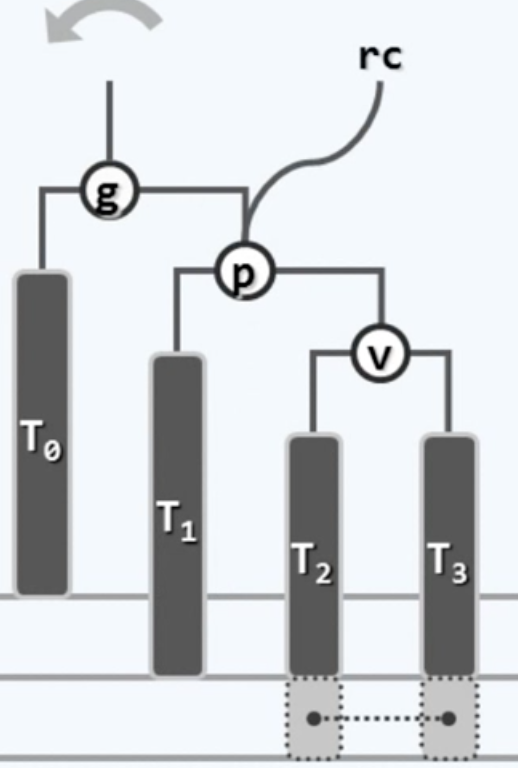
然后我们让T1成为g的右孩子，为此要这样调整：

接下来我们令g成为p的左孩子：

接下来我们要让局部子树的根由g变化为p，然后临时指针退休。

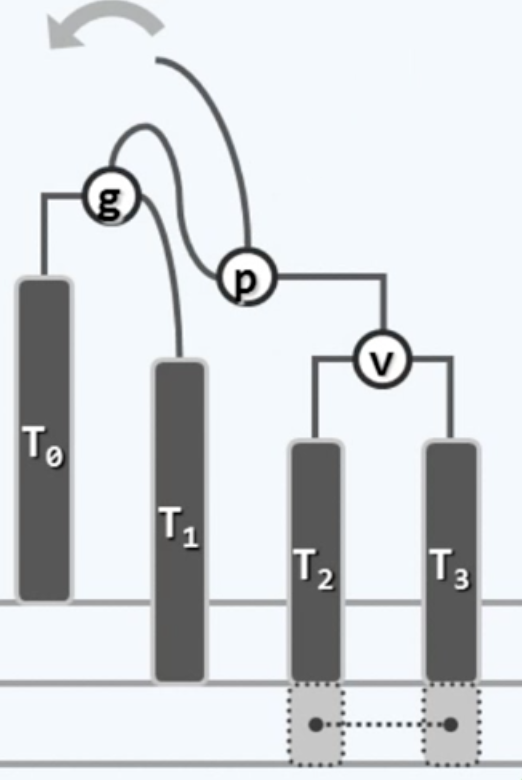
如此一来就完成了“右-右”的单旋转，整理一下就能看得更清了：

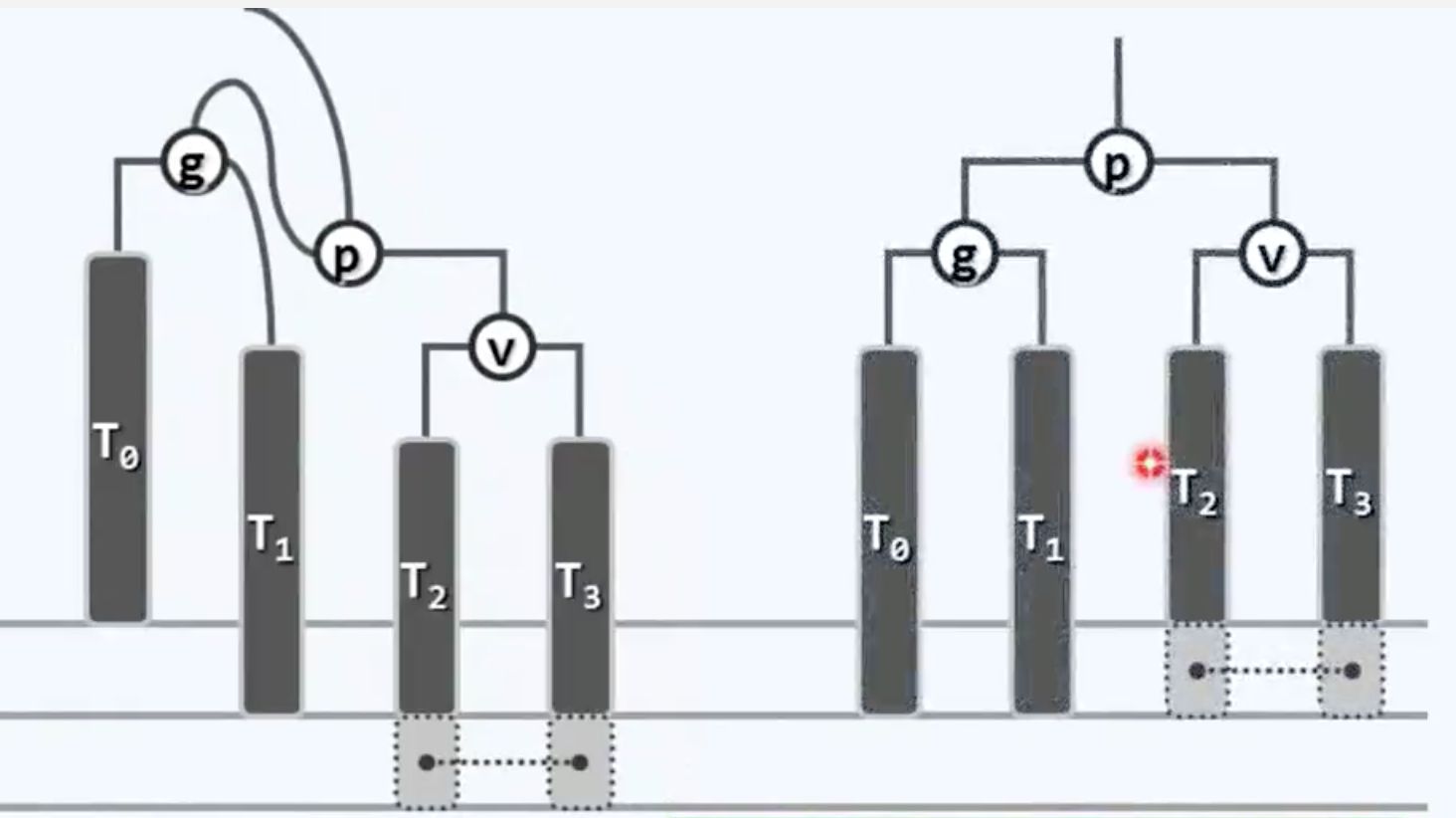
让我们把这个思路兑现为代码

/*
只有在 g 存在右孩子的情况下才被调用，在g和他的右孩子之间进行旋转操作。
最后要记得实时更新高度，返回当前的新树根
*/
static Position
SingleRotateWithRight( Position g )
{

    Position temp;

    temp = g->rc;
    g->rc = temp->lc;
    temp->lc = g;

    g->Height = max( Height( g->lc ), Height( g->rc ) ) + ;
    temp->Height = max( Height( temp->rc ), g->Height ) + ;

    return temp;  /* New root */
}

如果在此前g以上的祖先还有发生失衡，在这个局部重平衡之后，上面的各个节点也能一并恢复平衡。因为在这里除了平衡因子外，局部子树还有一个指标：高度。留意一下我们设置的三条基准线，在插入新节点之前，原树的高度以中线为基准，对照重新平衡后的树，它的高度又回到了中间的基准线上。那这又意味着什么呢？这意义十分重大，意味着他所有祖先在计算平衡因子时所得结果，也将与插入节点前完全一样，换而言之，上面的节点也都恢复平衡，那么全树都恢复了平衡。而我们只做了一次“右-右”旋转，只涉及常数个节点，时间消耗O（1），这再好不过了。

再说“左-左”旋转，也叫zig，比如对于这个局部

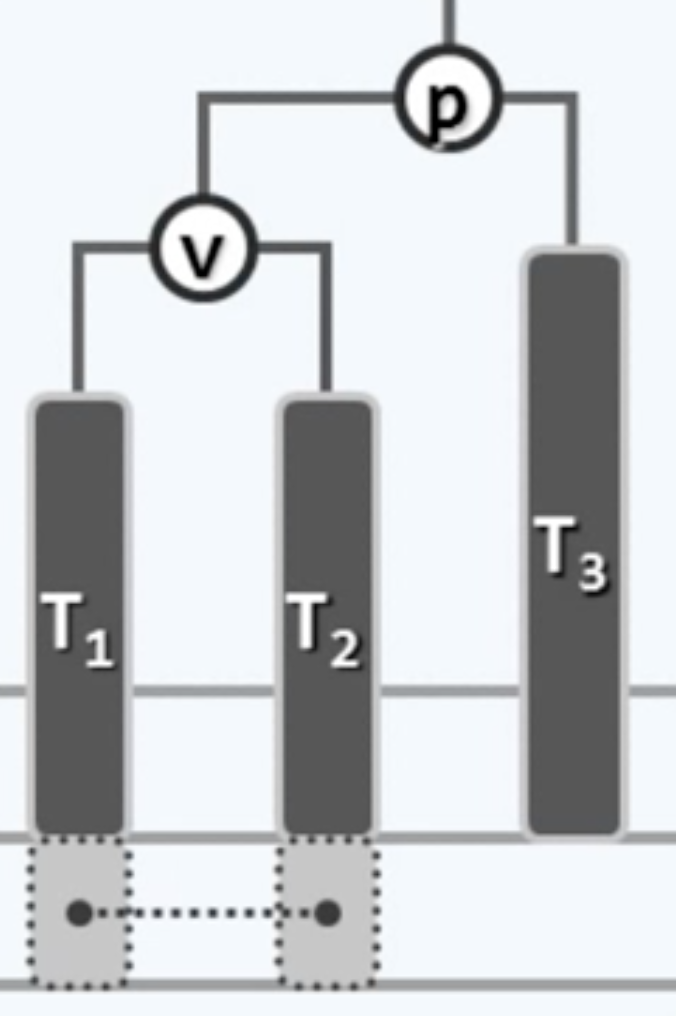
先用一个临时指针指向v

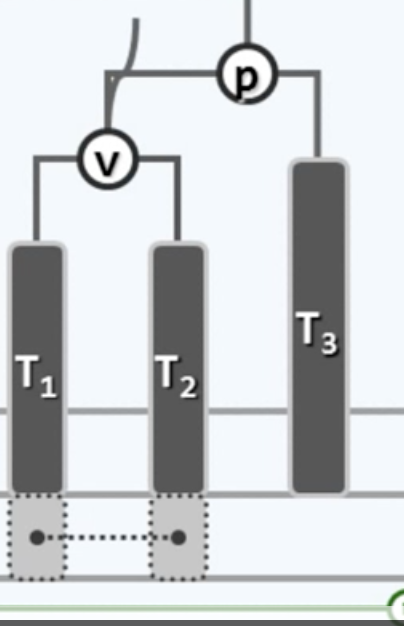
然后让T2成为p的左孩子

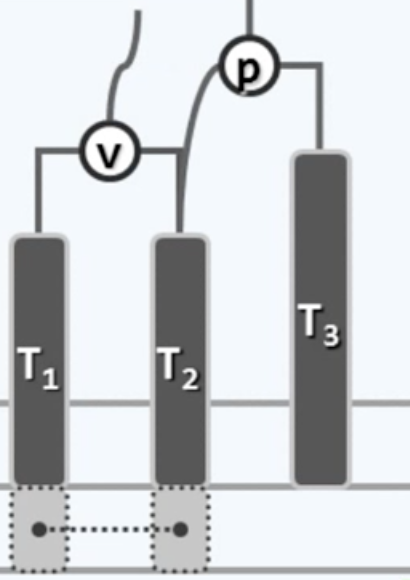
然后让p成为v的右孩子

最后把局部子树的根由p变更为v，临时指针下岗

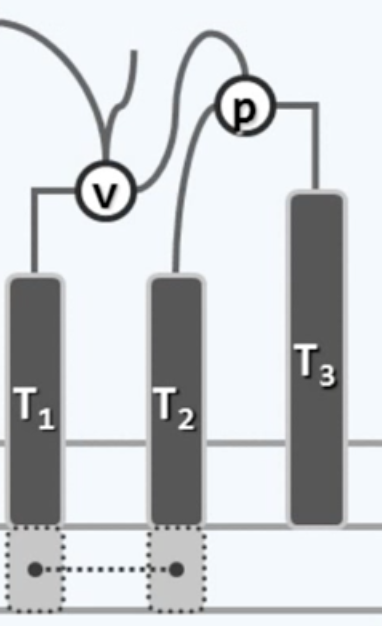
至此“左-左”旋转宣告完成，兑换为代码：

//仅当p存在左孩子时调用这个函数，更新高度并返回新的根

static Position
SingleRotateWithLeft( Position p )
{
    Position temp;

    temp = p->lc;
    p->lc = temp->rc;
    temp->rc = p;

    p->Height = max( Height( p->lc ), Height( p->rc ) ) + ;
    temp->Height = max( Height( temp->lc ), p->Height ) + ;

    return temp;  /* New root */
}

上面的算法有一个问题，就是解决的情况都是父子节点在朝向上是一致的，如果朝向不一致呢？单旋转就有心无力了，经过单旋转并不会降低它的深度，就需要引入第二种情况了：

内侧情形-双旋转

第二种情况是发生在内侧（左-右or右-左），这需要一次双旋转来完成，其实就是两个单旋转的组合，往往是方向相反的一组单旋转协同工作

先说右-左的情况，如下：

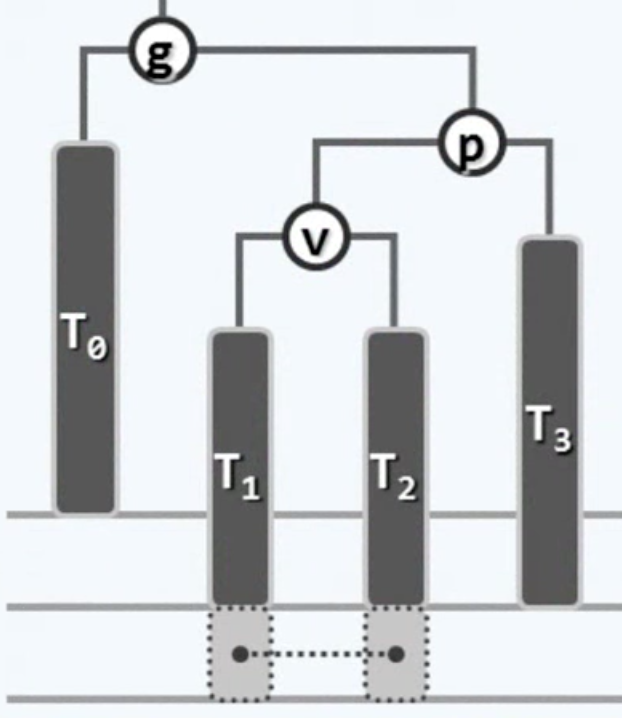
我们要抽丝剥茧地做重平衡操作，先看p-v这个局部，都朝向左边，所以首先的思路是对p执行一次顺时针的左-左的单旋转，就变成了这样：

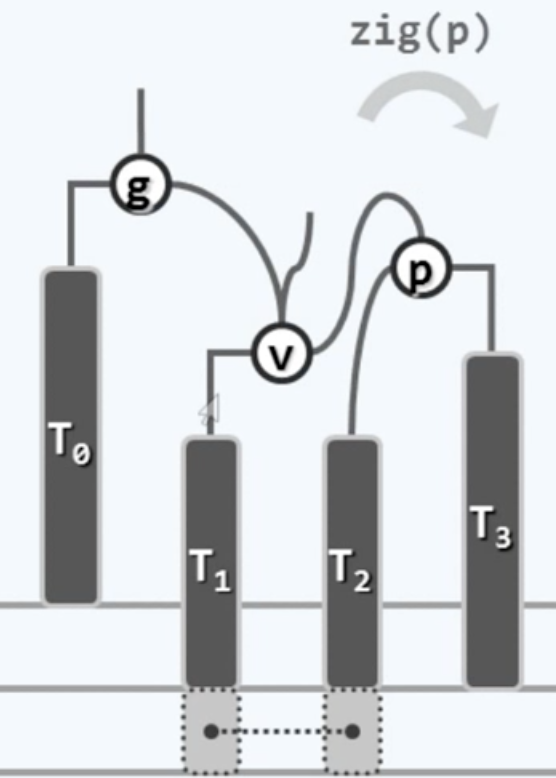
到这里，g,v,p三个节点就朝向一致了，那么显然，接下来我们要针对g做一次逆时针的zag旋转，和之前说的过程完全一样：

T1成为g的右孩子

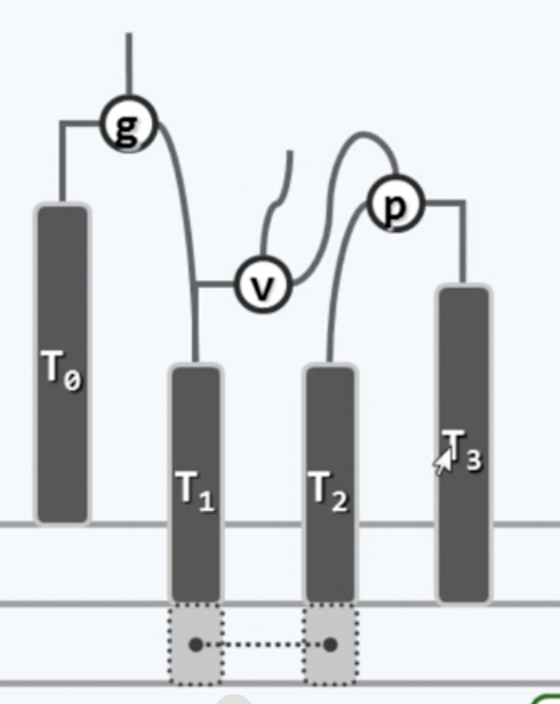
g成为v的左孩子（感觉这只蜘蛛要扑过来了2333）

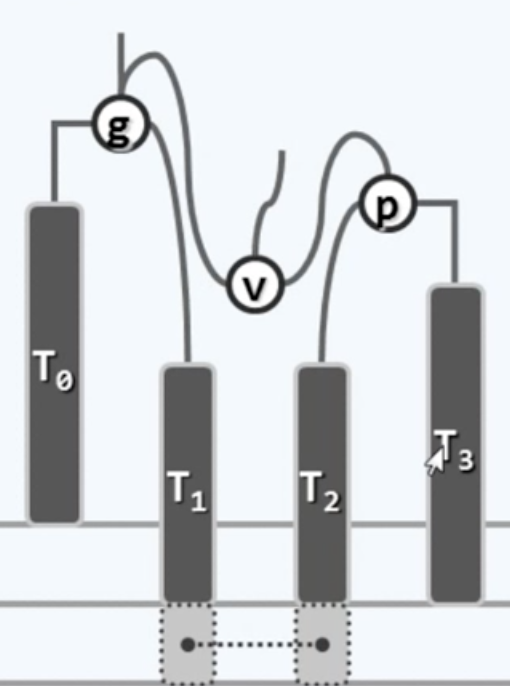
这样就完成了局部的重平衡，当然，这里再把细节展示出来是为了方便深入理解，实际写代码的时候直接调用对应单旋转操作，把g传进去就行了。为了清晰看出效果，做一下整理：

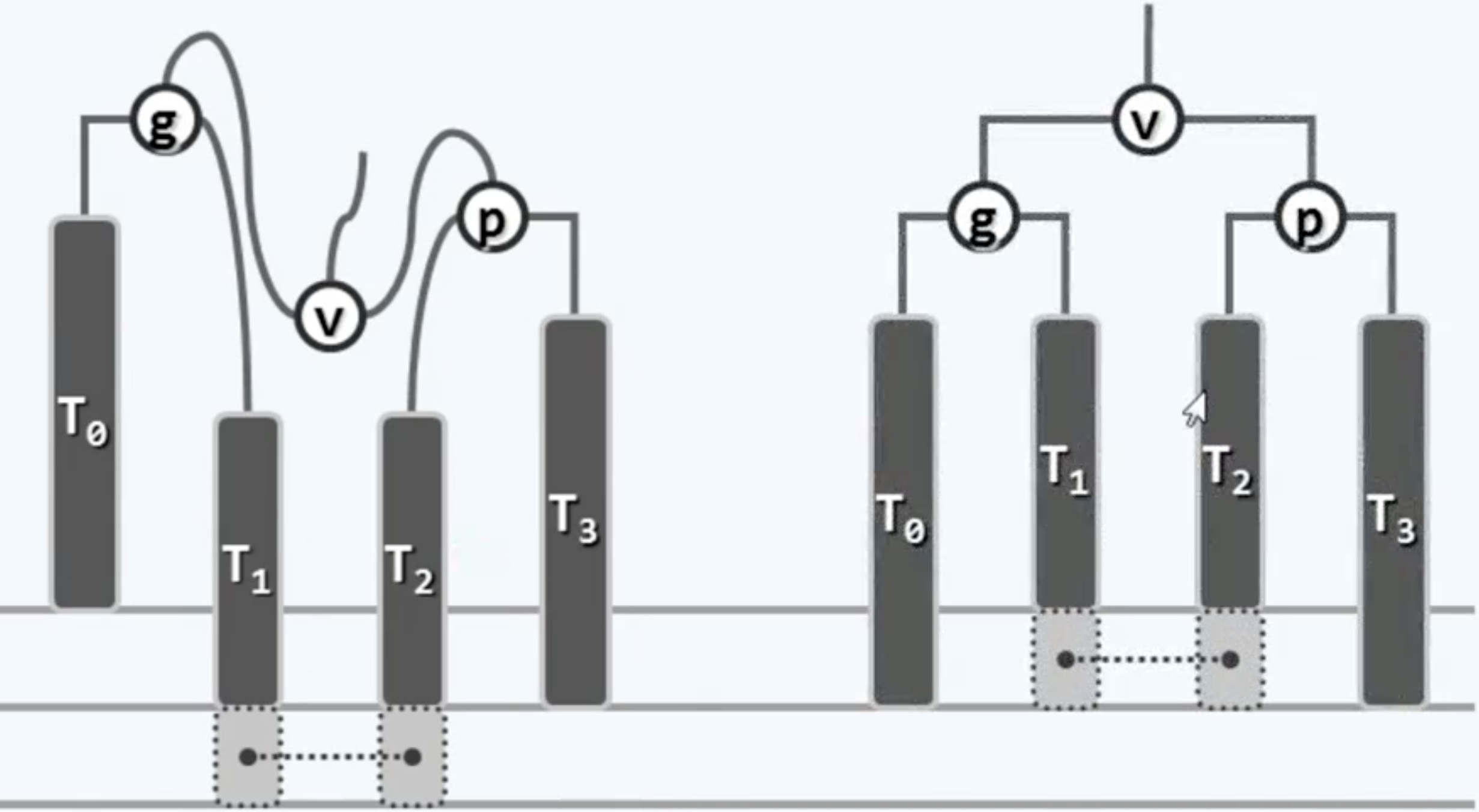
的确已经恢复平衡，以上可能失衡的祖先也会一并回复平衡。

// This function can be called only if g has a right
// child and g's right child has a left child
// Do the right-left double rotation
// Update heights, then return new root 

static Position
DoubleRotateWithRight( Position g )
{
    // Rotate between p and v, p means g->rc
    g->rc = SingleRotateWithLeft( g->rc );

    // Rotate between g and p
    return SingleRotateWithRight( g );
}

下面再说左-右旋转的情况：

为了重新平衡，就不能让k3继续是根了，不然高度永远降不下来。那么唯一的选择就是让k2作为新的根，如此一来根据BST的性质，我们必须把k1放在左孩子的位置上，k3放在右孩子的位置上。具体的做法是对k1,k2这个局部，由于父子朝向都向右，直觉也告诉我们要做一次右-右旋转：B成为k1的右孩子，k1这颗子树成为k2的左孩子。最后把k3的左孩子这颗子树的根变更为k2。

具体细微过程前面单旋转的时候说过了，这里就给出拆掉脚手架后的中间成品

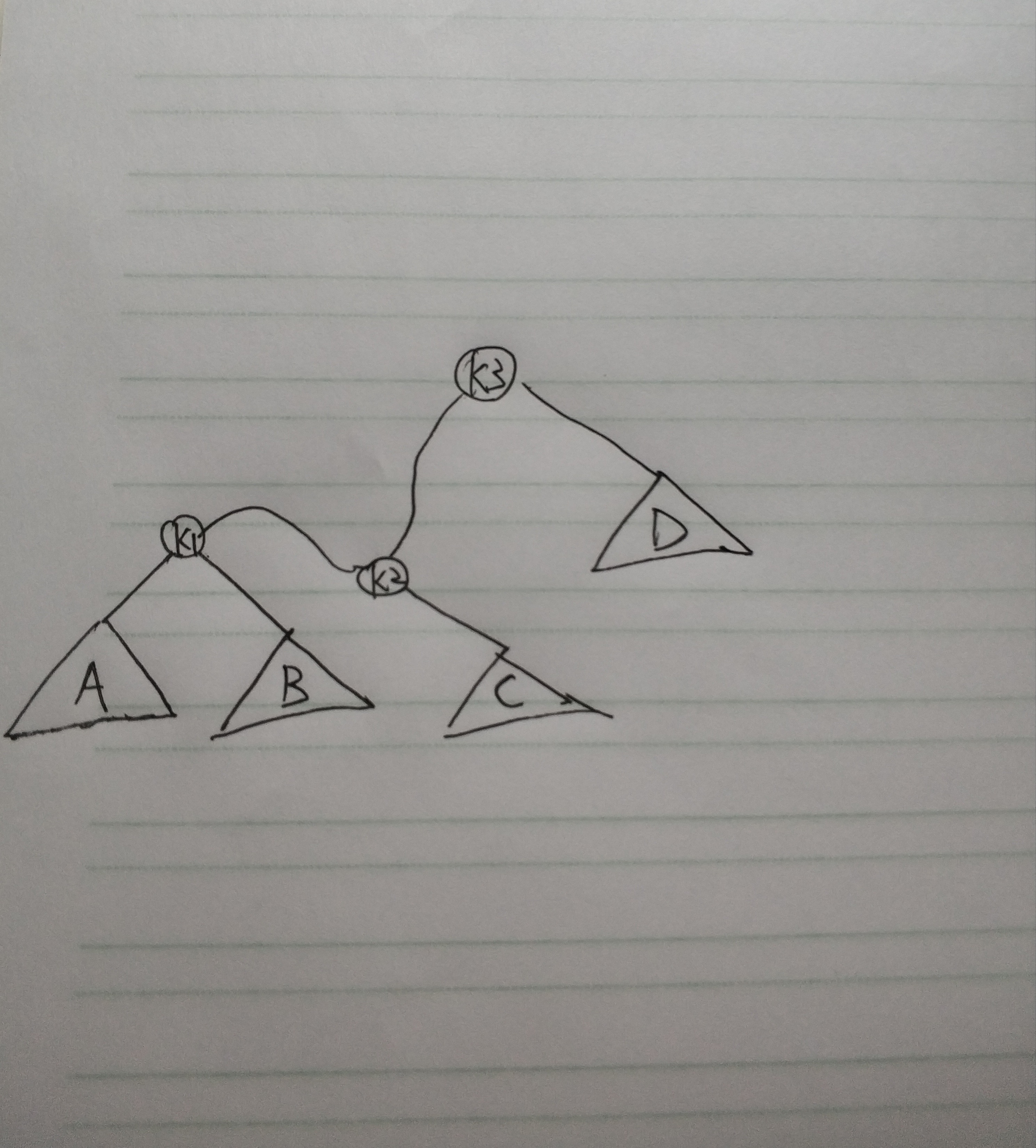
稍微整理一下就更明了了，把k2的高度提上去

到这一步之后，我们再把k3-k2这个局部，由于此时朝向都为左，那么顺理成章做一次左-左旋转：C成为k3的左孩

子，k3这颗子树成为k2的右孩子。至此，左-右旋转完成，全树的高度得到了控制。

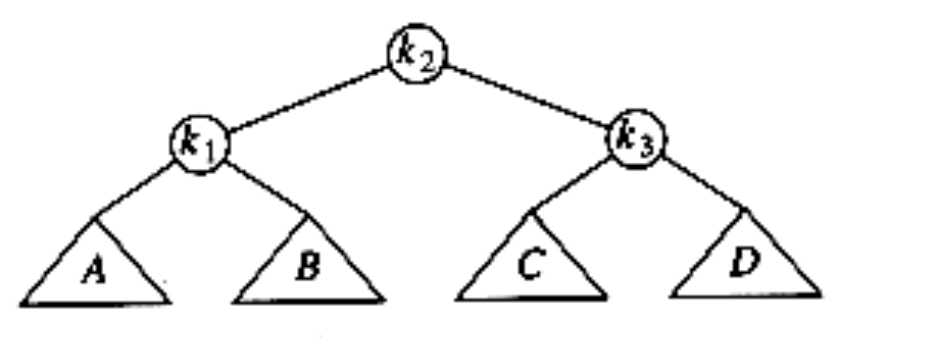
// This function can be called only if K3 has a left
// child and K3's left child has a right child
// Do the left-right double rotation
// Update heights, then return new root

static Position
DoubleRotateWithLeft( Position K3 )
{
    // Rotate between K1 and K2
    K3->lc = SingleRotateWithRight( K3->lc );

    // Rotate between K3 and K2
    return SingleRotateWithLeft( K3 );
}

这四种旋转策略已经覆盖了插入操作失衡的所有情况，下面给出总的插入操作，汇总了这四种情况。

AvlTree
Insert( int X, AvlTree T )
{
    if( !T ){//这里是实质的插入部分，无中生有
        //创建并返回一个单节点树
        T = (Position)malloc( sizeof( struct AvlNode ) );
        if( !T ) printf("Fatal Error: Out Of Space!\n");//错误检测
        else{
            T->value = X;
            T->Height = ;
            T->lc = T->rc = nullptr;
        }
    }

    //还未走到应插入的地点时
    else
        if( X < T->value ) //遵循BST的规则，new value < root value，往左走
        {
            T->lc = Insert( X, T->lc );//此时插入完成后，t指向被插入节点的父亲
            if( Height( T->lc ) - Height( T->rc ) ==  )
                 //如果新插入节点后lc比rc深2层，那么就是情形1，2
                if( X < T->lc->value )//如果是这样，根据BST规则，是左-左
                    T = SingleRotateWithLeft( T );
                else //否则是左-右
                    T = DoubleRotateWithLeft( T );
         /*
          我们需要根据情况去采取不同的旋转策略，使其恢复平衡
          单旋转调整了情形1:发生在外侧，对a的lc->lc插入
          双旋转调整了情形2:发生在内侧，对a的lc->rc插入
          */

        }
        else
            if( X > T->value )
            {
                T->rc = Insert( X, T->rc );
                //遵循BST的规则，new value > root value，往右走

                if( Height( T->rc ) - Height( T->lc ) ==  )
                    //如果新插入节点后右子树更高，那么就是情形3，4
                    if( X > T->rc->value )  //如果是这样，根据BST规则，是右-右
                        T = SingleRotateWithRight( T );
                    else //否则是右-左
                        T = DoubleRotateWithRight( T );
                /*
                 这个分支里
                 单旋转调整了情形3:发生在外侧，对a的rc->rc插入
                 双旋转调整了情形4:发生在内侧，对a的rc->lc插入
                */
            }

    /* Else X is in the tree already; we'll do nothing */

    T->Height = max( Height( T->lc ), Height( T->rc ) ) + ;
    return T;
}

最后可以做一个很直观的比较：分别构建大数据量的BST和AVLT，比较他们的高度，就可以明显看出平衡操作对于高度的有效控制了，给一个完整版本的实现吧，可以对比下和普通BST的层数差距。

 #include "avltree.h"  //这里只给出.c的部分，头文件就是前文的类型声明+各种函数签名
 #include <stdlib.h>
 #include <stdio.h>
 #include <time.h>

 int max(int a,int b){return a>b?a:b;}

 int updateH(AvlTree x){
     return x->Height =  + max ( Height ( x->lc ), Height ( x->rc ) );
 }

 AvlTree
 MakeEmpty( AvlTree T )
 {
     if( T != NULL )
     {
         MakeEmpty( T->lc );
         MakeEmpty( T->rc );
         free( T );
     }
     return NULL;
 }

 void Preorder(Position root);

 int main() {
     srand(time(NULL));
     AvlTree a=nullptr;
     int nodeCnt,del;
     printf("Please input how many nodes in the avl tree: ");
     scanf("%d",&nodeCnt);
     for(int i=;i<nodeCnt;i++) a=Insert(rand()%(nodeCnt<<), a);
     Preorder(a);
     printf("\n\nThe height of avlt with %d nodes is : %d\n",nodeCnt,Height(a));
 //    scanf("%d",&del);
 //    DeleteInAVL(del, a);
 //    Preorder(a);
 }

 Position
 Find( int X, AvlTree T )
 {
     if( !T )
         return NULL;
     if( X < T->value ){
         return Find( X, T->lc );
     }
     else
         if( X > T->value )
             return Find( X, T->rc );
         else
             return T;
 }

 Position
 FindMin( AvlTree T )
 {
     if( !T )
         return NULL;
     else
         if( T->lc == NULL )
             return T;
         else
             return FindMin( T->lc );
 }

 Position
 FindMax( AvlTree T )
 {
     if( T != NULL )
         while( T->rc != NULL )
             T = T->rc;

     return T;
 }

 // This function can be called only if g has a left child
 // Perform a rotate between a node (g) and its left child
 // Update heights, then return new root

 static Position
 SingleRotateWithLeft( Position p )   //左-左的情况
 {
     Position temp;

     temp = p->lc;
     p->lc = temp->rc;

     temp->rc = p; 

     p->Height = max( Height( p->lc ), Height( p->rc ) ) + ;
     temp->Height = max( Height( temp->lc ), p->Height ) + ;

     return temp;  /* New root */
 }

 // This function can be called only if g has a right child
 // Perform a rotate between a node (g) and its right child
 // Update heights, then return new root

 static Position
 SingleRotateWithRight( Position g )   //右-右的情况
 {
     Position temp;

     temp = g->rc;
     g->rc = temp->lc;

     temp->lc = g;     

     g->Height = max( Height( g->lc ), Height( g->rc ) ) + ;
     temp->Height = max( Height( temp->rc ), g->Height ) + ;

     return temp;  /* New root */
 }

 // This function can be called only if K3 has a left
 // child and K3's left child has a right child
 // Do the left-right double rotation
 // Update heights, then return new root

 static Position
 DoubleRotateWithLeft( Position K3 )   //左-右的情况
 {
     /* Rotate between K1 and K2 */
     K3->lc = SingleRotateWithRight( K3->lc );

     /* Rotate between K3 and K2 */
     return SingleRotateWithLeft( K3 );
 }

 // This function can be called only if g has a right
 // child and g's right child has a left child
 // Do the right-left double rotation
 // Update heights, then return new root

 static Position
 DoubleRotateWithRight( Position g )   //右-左的情况
 {
     // Rotate between p and v, p means g->rc
     g->rc= SingleRotateWithLeft( g->rc );

     // Rotate between g and p
     return SingleRotateWithRight( g );
 }

 AvlTree
 Insert( int X, AvlTree T )
 {
     Position p;// it means p on the "new node"
     if( !T ){//这里是实质的插入部分，无中生有
         //创建并返回一个单节点树
         T = (Position)malloc( sizeof( struct AvlNode ) );
         if( !T ) printf("Fatal Error: Out Of Space!\n");//错误检测
         else{
             T->value = X;
             T->Height = ;
             T->lc = T->rc = nullptr;
         }
     }

     //还未走到应插入的地点时
     else
         if( X < T->value ) //遵循BST的规则，new value < root value，往左走
         {
             T->lc = Insert( X, T->lc );
             //此时插入完成后，T指向被插入节点的父亲,新生节点作为T的左孩子而存在。

             if( Height(T->lc)-Height(T->rc) ==  )
                 //如果新插入节点后lc比rc深2层，那么就是情形1，2
                 if( X < T->lc->value )//如果是这样，根据BST规则，是左-左
                     T = SingleRotateWithLeft( T );
                 else //否则是左-右
                     T = DoubleRotateWithLeft( T );
             /*
              我们需要根据情况去采取不同的旋转策略，使其恢复平衡
              单旋转调整了情形1:发生在外侧，对a的lc->lc插入
              双旋转调整了情形2:发生在内侧，对a的lc->rc插入
              */

         }
         else
             if( X > T->value ) //遵循BST的规则，new value > root value，往右走
             {
                 T->rc = Insert( X, T->rc );
                 //此时插入完成后，T指向被插入节点的父亲,新生节点作为T的右孩子而存在。
                 if( Height(T->rc)-Height(T->lc) ==  )
                     //如果新插入节点后右子树更高，那么就是情形3，4
                     if( X > T->rc->value )  //如果是这样，根据BST规则，是右-右
                         T = SingleRotateWithRight( T );
                     else //否则是右-左
                         T = DoubleRotateWithRight( T );
                 /*
                  这个分支里
                  单旋转调整了情形3:发生在外侧，对a的rc->rc插入
                  双旋转调整了情形4:发生在内侧，对a的rc->lc插入
                  */

                 //
             }

     /* Else X is in the tree already; we'll do nothing */

     updateH(T);
     return T;
 }

 int
 Retrieve( Position P )
 {
     return P->value;
 }

 void Preorder(Position root){
     if (root) {
         printf("%d ",root->value);
         Preorder(root->lc);
         Preorder(root->rc);
     }
 }

祝食用愉快2333

ps.转载请注明文章来源，否则会追加法律责任。