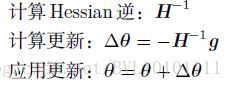Deep Learning 之 最优化方法
Deep Learning 之 最优化方法
写在前面本文主要是对Deep Learning一书最优化方法的总结,具体详细的算法,另起博文展开。
整个优化系列文章列表:
Deep Learning 最优化方法之Momentum(动量)
深度学习中,经常需要用到优化方法,来寻找使得损失函数最小的最优解。
先上一些结论:
1.选择哪种优化算法并没有达成共识
2.具有自适应学习率(以RMSProp 和AdaDelta 为代表)的算法族表现得相当鲁棒,不分伯仲,但没有哪个算法能脱颖而出。
3.对于当前流行的优化算法包括括SGD、具动量的SGD、RMSProp、具动量的RMSProp、AdaDelta 和Adam而言,选择哪一个算法似乎主要取决于使用者对算法的熟悉程度(以便调节超参数)
4.基本不用二阶近似优化算法
在这里将这些优化方法分为三类,详见对应的blog:
一.最基本的优化算法
1.1SGD
SGD实际就是min-batch的实现,为最基础的优化算法,当今大部分优化算法都是以SGD为基础实现的。详见Deep Learning 最优化方法之SGD
1.2Momentum(动量)
Momentum引入了动量v,以指数衰减的形式累计历史梯度,以此来解决Hessian矩阵病态问题
详见Deep Learning 最优化方法之Momentum(动量)
1.3Nesterov(牛顿动量)
Nesterov是对Momentum的变种。与Momentum不同的是,Nesterov先更新参数,再计算梯度
详见Deep Learning 最优化方法之Nesterov(牛顿动量)
二.自适应参数的优化算法
这类算法最大的特点就是,每个参数有不同的学习率,在整个学习过程中自动适应这些学习率。
2.1AdaGrad
学习率逐参数的除以历史梯度平方和的平方根,使得每个参数的学习率不同
详见Deep Learning 最优化方法之AdaGrad
2.2RMSProp
AdaGrad算法的改进。
历史梯度平方和—>指数衰减的移动平均,以此丢弃遥远的过去历史。
详见Deep Learning 最优化方法之RMSProp
2.3Adam
Adam算法可以看做是修正后的Momentum+RMSProp算法
详见Deep Learning 最优化方法之Adam
三.二阶近似的优化算法
二阶近似作为早期处理神经网络的方法,在此并不另起blog展开细讲。
3.1牛顿法
牛顿法是基于二阶泰勒级数展开在某点附近来近似损失函数的优化方法。主要需要求得Hessian矩阵的逆。如果参数个数是k,则计算你所需的时间是O(k^3)由于在神经网络中参数个数往往是巨大的,因此牛顿法计算法消耗时间巨大。
具体更新公式如下:
3.2共轭梯度法
共轭梯度(CG)是通过迭代下降的共轭方向(conjugate directions)以有效避免Hessian 矩阵求逆计算的方法。
- 1
- 2
3.3BFGS
Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法具有牛顿法的一些优点,但没有牛顿法的计算负担。在这方面,BFGS和CG 很像。然而,BFGS使用了一个更直接的方法近似牛顿更新。用矩阵Mt 近似逆,迭代地低秩更新精度以更好地近似Hessian的逆。
- 1
- 2
3.4L-BFGS
存储受限的BFGS(L-BFGS)通过避免存储完整的Hessian 逆的近似矩阵M,使得BFGS算法的存储代价显著降低。L-BFGS算法使用和BFGS算法相同的方法计算M的近似,但起始假设是M^(t-1) 是单位矩阵,而不是一步一步都要存储近似。
- 1
- 2
Deep Learning 之 最优化方法的更多相关文章
- 中文译文:Minerva-一种可扩展的高效的深度学习训练平台(Minerva - A Scalable and Highly Efficient Training Platform for Deep Learning)
Minerva:一个可扩展的高效的深度学习训练平台 zoerywzhou@gmail.com http://www.cnblogs.com/swje/ 作者:Zhouwan 2015-12-1 声明 ...
- Deep learning:五十一(CNN的反向求导及练习)
前言: CNN作为DL中最成功的模型之一,有必要对其更进一步研究它.虽然在前面的博文Stacked CNN简单介绍中有大概介绍过CNN的使用,不过那是有个前提的:CNN中的参数必须已提前学习好.而本文 ...
- 【深度学习Deep Learning】资料大全
最近在学深度学习相关的东西,在网上搜集到了一些不错的资料,现在汇总一下: Free Online Books by Yoshua Bengio, Ian Goodfellow and Aaron C ...
- 《Neural Network and Deep Learning》_chapter4
<Neural Network and Deep Learning>_chapter4: A visual proof that neural nets can compute any f ...
- Deep Learning模型之:CNN卷积神经网络(一)深度解析CNN
http://m.blog.csdn.net/blog/wu010555688/24487301 本文整理了网上几位大牛的博客,详细地讲解了CNN的基础结构与核心思想,欢迎交流. [1]Deep le ...
- paper 124:【转载】无监督特征学习——Unsupervised feature learning and deep learning
来源:http://blog.csdn.net/abcjennifer/article/details/7804962 无监督学习近年来很热,先后应用于computer vision, audio c ...
- Deep Learning 26:读论文“Maxout Networks”——ICML 2013
论文Maxout Networks实际上非常简单,只是发现一种新的激活函数(叫maxout)而已,跟relu有点类似,relu使用的max(x,0)是对每个通道的特征图的每一个单元执行的与0比较最大化 ...
- Deep Learning 23:dropout理解_之读论文“Improving neural networks by preventing co-adaptation of feature detectors”
理论知识:Deep learning:四十一(Dropout简单理解).深度学习(二十二)Dropout浅层理解与实现.“Improving neural networks by preventing ...
- Deep Learning 19_深度学习UFLDL教程:Convolutional Neural Network_Exercise(斯坦福大学深度学习教程)
理论知识:Optimization: Stochastic Gradient Descent和Convolutional Neural Network CNN卷积神经网络推导和实现.Deep lear ...
随机推荐
- P2341 [HAOI2006]受欢迎的牛 强连通
题目背景 本题测试数据已修复. 题目描述 每头奶牛都梦想成为牛棚里的明星.被所有奶牛喜欢的奶牛就是一头明星奶牛.所有奶 牛都是自恋狂,每头奶牛总是喜欢自己的.奶牛之间的“喜欢”是可以传递的——如果A喜 ...
- Docker 常用指令
1.检查内核版本,必须是3.10及以上uname ‐r2.安装dockeryum install docker3.输入y确认安装4.启动docker[root@localhost ~]# system ...
- 使用maven创建项目
http://192.168.4.112/rdmanager/main/index.jhtml 1.对于第一次下载某个项目的源码,按照下面的步骤进行: (1)在D:\projects\目录下的空白位置 ...
- PHP中级面试经历
资源来自网络:http://www.2cto.com/kf/201304/204749.html 1.用PHP打印出前一天的时间格式是2006-5-10 22:21:21(2分) 2.echo(),p ...
- python 通过 socket 发送文件
目录结构: client: #!/usr/bin/env python # -*-coding:utf-8 -*- import socket, struct, json download_dir = ...
- mysql数据去重复distinct、group by
使用distinct 和group by都可以实现数据去重. select distinct 字段 group by 一般放在where条件后
- select 文字右对齐
select { direction: rtl; } select option { direction: ltr; }
- 全文搜索引擎 Elasticsearch 安装踩坑记录
一.安装 Elastic 需要 Java 8 环境.如果你的机器还没安装 Java 安装完 Java,就可以跟着官方文档安装 Elastic.直接下载压缩包比较简单. $ wget https://a ...
- c# 一种缓存模板
在很多项目中,尤其是服务端,我们需要临时缓存一些数据,对于完整的我就不说了.主要的保持方法有: 1.大型数据库 2.缓存组件 3.文件(按照自己定义的格式存储) 4.一些缓存数据库(sqlte,h2, ...
- js面向对象轮播图写法
;;} ,,,;} ]; ].].; ){ ; ; }) } Banner.protot ...