最长公共子序列PK最长公共子串

1、先科普下最长公共子序列 & 最长公共子串的区别：

找两个字符串的最长公共子串，这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。

(1)递归方法求最长公共子序列的长度

　　　　1)设有字符串a[0...n]，b[0...m]，下面就是递推公式。

当数组a和b对应位置字符相同时，则直接求解下一个位置；当不同时取两种情况中的较大数值。

　　　　

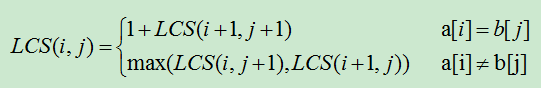
　　　　2)代码如下：

 #include<stdio.h>
 #include<string.h>
 char a[30],b[30];
 int lena,lenb;
 int LCS(int,int);　　///两个参数分别表示数组a的下标和数组b的下标
 
 int main()
 {
     strcpy(a,"ABCBDAB");
     strcpy(b,"BDCABA");
     lena=strlen(a);
     lenb=strlen(b);
     printf("%d\n",LCS(0,0));
     return 0;
 }
 
 int LCS(int i,int j)
 {
     if(i>=lena || j>=lenb)
         return 0;
     if(a[i]==b[j])
         return 1+LCS(i+1,j+1);
     else
         return LCS(i+1,j)>LCS(i,j+1)? LCS(i+1,j):LCS(i,j+1);
 }

用递归的方法优点是编程简单，容易理解。缺点是效率不高，有大量的重复执行递归调用，而且只能求出最大公共子序列的长度，求不出具体的最大公共子序列。

　　(2)动态规划求最长公共子序列的长度

　　　　动态规划采用二维数组来标识中间计算结果，避免重复的计算来提高效率。

　　　　1)最长公共子序列的长度的动态规划方程

　　　　设有字符串a[0...n]，b[0...m]，下面就是递推公式。字符串a对应的是二维数组num的行，字符串b对应的是二维数组num的列。

　　　　

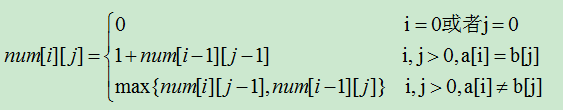
代码如下：

 #include<stdio.h>
 #include<string.h>
 
 char a[500],b[500];
 char num[501][501]; ///记录中间结果的数组
 char flag[501][501];    ///标记数组，用于标识下标的走向，构造出公共子序列
 void LCS(); ///动态规划求解
 void getLCS();    ///采用倒推方式求最长公共子序列
 
 int main()
 {
     int i;
     strcpy(a,"ABCBDAB");
     strcpy(b,"BDCABA");
     memset(num,0,sizeof(num));
     memset(flag,0,sizeof(flag));
     LCS();
     printf("%d\n",num[strlen(a)][strlen(b)]);
     getLCS();
     return 0;
 }
 
 void LCS()
 {
     int i,j;
     for(i=1;i<=strlen(a);i++)
     {
         for(j=1;j<=strlen(b);j++)
         {
             if(a[i-1]==b[j-1])   ///注意这里的下标是i-1与j-1
             {
                 num[i][j]=num[i-1][j-1]+1;
                 flag[i][j]=1;  ///斜向下标记
             }
             else if(num[i][j-1]>num[i-1][j])
             {
                 num[i][j]=num[i][j-1];
                 flag[i][j]=2;  ///向右标记
             }
             else
             {
                 num[i][j]=num[i-1][j];
                 flag[i][j]=3;  ///向下标记
             }
         }
     }
 }
 
 void getLCS()
 {
 
     char res[500];
     int i=strlen(a);
     int j=strlen(b);
     int k=0;    ///用于保存结果的数组标志位
     while(i>0 && j>0)
     {
         if(flag[i][j]==1)   ///如果是斜向下标记
         {
             res[k]=a[i-1];
             k++;
             i--;
             j--;
         }
         else if(flag[i][j]==2)  ///如果是斜向右标记
             j--;
         else if(flag[i][j]==3)  ///如果是斜向下标记
             i--;
     }
 
     for(i=k-1;i>=0;i--)
         printf("%c",res[i]);
 }

(3)图示

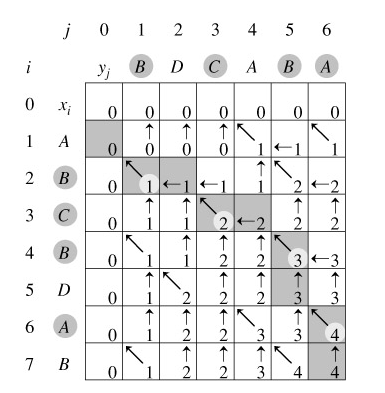
最长公共子串

 import java.util.Scanner;
 
 public class Main {
     public static void main(String[] args) {
         Scanner sc = new Scanner(System.in);
         Main mainObj = new Main();
         int len = mainObj.getCommonStrLength(sc.next(),sc.next());
         System.out.println(len);
     }
 
     int getCommonStrLength(String str1, String str2) {
              str1 = str1.toLowerCase();
             str2 = str2.toLowerCase();
             int len1 = str1.length();
             int len2 = str2.length();
             String min = null;
             String max = null;
             String target = null;
             min = len1 <= len2 ? str1 : str2;
             max = len1 >  len2 ? str1 : str2;
             //最外层：min子串的长度，从最大长度开始
             for (int i = min.length(); i >= 1; i--) {
                 //遍历长度为i的min子串，从0开始
                 for (int j = 0; j <= min.length() - i; j++) {
                     target = min.substring(j, j + i);
                     //遍历长度为i的max子串，判断是否与target子串相同，从0开始
                     for (int k = 0; k <= max.length() - i; k++) {
                         if (max.substring(k,k + i).equals(target)) {
                             return i;
                         }
                     }
                 }
             }
             return 0;
     }
 }