纸上谈兵：图（graph）

作者：Vamei 出处：http://www.cnblogs.com/vamei 欢迎转载，也请保留这段声明。谢谢！

图(graph)是一种比较松散的数据结构。它有一些节点(vertice)，在某些节点之间，由边(edge)相连。节点的概念在树中也出现过，我们通常在节点中储存数据。边表示两个节点之间的存在关系。在树中，我们用边来表示子节点和父节点的归属关系。树是一种特殊的图，但限制性更强一些。

这样的一种数据结构是很常见的。比如计算机网络，就是由许多节点(计算机或者路由器)以及节点之间的边(网线)构成的。城市的道路系统，也是由节点(路口)和边(道路)构成的图。地铁系统也可以理解为图，地铁站可以认为是节点。基于图有许多经典的算法，比如求图中两个节点的最短路径，求最小伸展树等。

图的经典研究是柯尼斯堡七桥问题(Seven Bridges of Königsberg)。柯尼斯堡是现今的加里宁格勒，城市中有一条河流过，河中有两个小岛。有七座桥桥连接河的两岸和两个小岛。送信员总想知道，有没有一个办法，能不重复的走过7个桥呢？

(这个问题在许多奥数教材中称为"一笔画"问题)

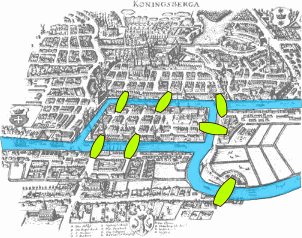
欧拉时代的柯尼斯堡地图

柯尼斯堡的可以看作由7个边和4个节点构成的一个图:

这个问题最终被欧拉巧妙的解决。七桥问题也启发了一门新的数学学科——图论(graph theory)的诞生。欧拉的基本思路是，如果某个节点不是起点或者终点，那么连接它的边的数目必须为偶数个(从一个桥进入，再从另一个桥离开)。对于柯尼斯堡的七桥，由于4个节点都为奇数个桥，而最多只能有两个节点为起点和终点，所以不可能一次走完。

图的定义

严格的说，图G=(V,E)是由节点的集合V和边的集合E构成的。一个图的所有节点构成一个集合V。一个边可以表示为(v1,v2)，其中v1,v2∈V，即两个节点。如果(v1,v2)有序，即(v1,v2)与(v2,v1)不同，那么图是有向的(directed)。有序的边可以理解为单行道，只能沿一个方向行进。如果(v1,v2)无序，那么图是无向的(undirected)。无序的边可以理解成双向都可以行进的道路。一个无序的边可以看作连接相同节点的两个反向的有序边，所以无向图可以理解为有向图的一种特殊情况。

(七桥问题中的图是无向的。城市中的公交线路可以是无向的，比如存在单向环线)

图的一个路径(path)是图的一系列节点w1,w2,...,wn，且对于1≤i<n，有(wi,wi+1)∈E。也就是说，路径是一系列的边连接而成，路径的两端为两个节点。路径上边的总数称为路径的长度。乘坐地铁时，我们会在选择某个路径，来从A站到达B站。这样的路径可能有不止一条，我们往往会根据路径的长度以及沿线的拥挤状况，来选择一条最佳的路线。如果存在一条长度大于0的路径，该路径的两端为同一节点，那么认为该图中存在环路(cycle)。很明显，上海的地铁系统中存在环路。

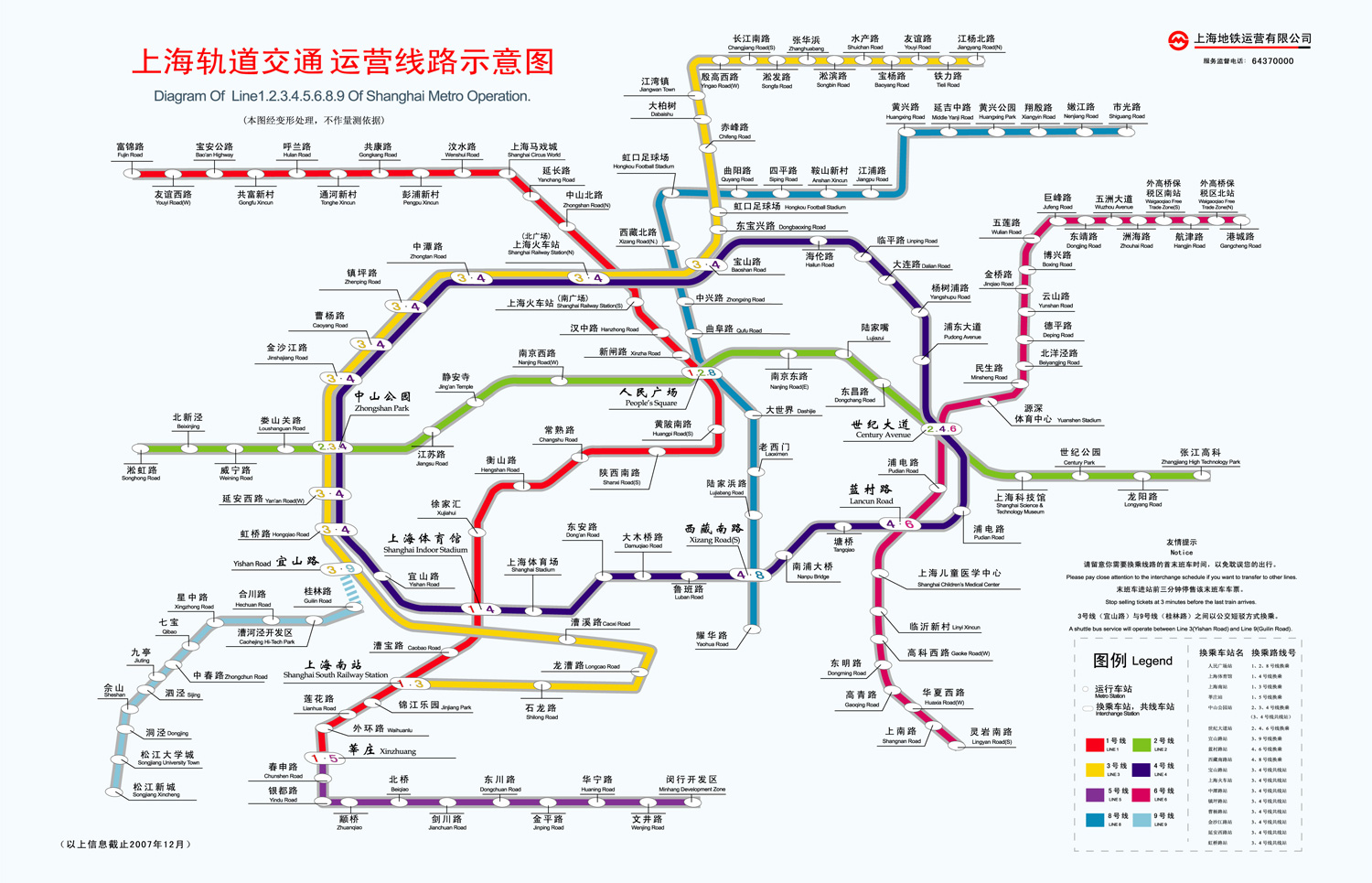
找到一条环路

如果从每个节点，到任意一个其它的节点，都有一条路径的话，那么图是连通的(connected)。对于一个有向图来说，这样的连通称为强连通(strongly connected)。如果一个有向图不满足强连通的条件，但将它的所有边都改为双向的，此时的无向图是连通的，那么认为该有向图是弱连通(weakly connected)。

如果将有火车站的城市认为是节点，铁路是连接城市的边，这样的图可能是不连通的。比如北京和费城，北京有铁路通往上海，费城有铁路通往纽约，但北京和费城之间没有路径相连。

图的实现

一种简单的实现图的方法是使用二维数组。让数组a的每一行为一个节点，该行的不同元素表示该节点与其他节点的连接关系。如果(u,v)∈E，那么a[u][v]记为1，否则为0。比如下面的一个包含三个节点的图:

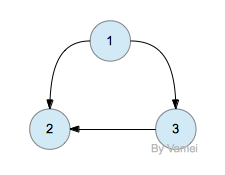
可以简单表示为

a	1	2	3
1	0	1	1
2	0	0	0
3	0	1	0

这种实现方式所占据的空间为O(|V|2)，|V|为节点总数。所需内存随着节点增加而迅速增多。如果边不是很密集，那么很多数组元素记为0，只有稀疏的一些数组元素记为1，所以并不是很经济。

更经济的实现方式是使用邻接表(adjacency list)，即记录每个节点所有的相邻节点。对于节点m，我们建立一个链表。对于任意节点k，如果有(m,k)∈E，就将该节点放入到对应节点m的链表中。邻接表是实现图的标准方式。比如下面的图，

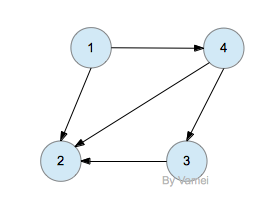
可以用如下的数据结构实现：

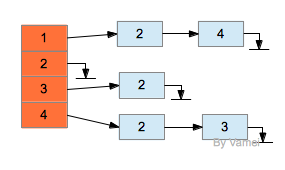
左侧为一个数组，每个数组元素代表一个节点，且指向一个链表。该链表包含有该数组元素所有的相邻元素。

总体上看，邻接表可以分为两部分。邻接表所占据的总空间为O(|V|+|E|)。数组部分储存节点信息，占据|V|)的空间，即节点的总数。链表存储边的信息，占据|E|的空间，即边的总数。在一些复杂的问题中，定点和边还可能有其他的附加信息，我们可以将这些附加信息储存在相应的节点或者边的位置。

下面为具体的C代码:

/* By Vamei */
#include <stdio.h>
#include <stdlib.h>

#define NUM_V 5

typedef struct node *position;

/* node */
struct node {
    int element;
    position next;
};

/*
 * operations (stereotype)
 */
void insert_edge(position, int, int);
void print_graph(position graph, int nv);

/* for testing purpose */
void main()
{
    struct node graph[NUM_V];
    int i;

    // initialize the vertices
    for(i=1; i<NUM_V; i++) {
        (graph+i)->element = i;
        (graph+i)->next    = NULL;
    }

    // insert edges
    insert_edge(graph,1,2);
    insert_edge(graph,1,4);
    insert_edge(graph,3,2);
    insert_edge(graph,4,2);
    insert_edge(graph,4,3);

    print_graph(graph,NUM_V);
}

/* print the graph */
void print_graph(position graph, int nv) {
    int i;
    position p;
    for(i=1; i<nv; i++) {
        p = (graph + i)->next;
        printf("From %3d: ", i);
        while(p != NULL) {
            printf("%d->%d; ", i, p->element);
            p = p->next;
        }
        printf("\n");
    }
}

/*
 * insert an edge
 */
void insert_edge(position graph,int from, int to)
{
    position np;
    position nodeAddr;

    np = graph + from;

    nodeAddr = (position) malloc(sizeof(struct node));
    nodeAddr->element = to;
    nodeAddr->next    = np->next;
    np->next = nodeAddr;
}

运行结果:

From   1: 1->4; 1->2; 
From   2: 
From   3: 3->2; 
From   4: 4->3; 4->2;

上面的实现主要基于链表，可参考纸上谈兵: 表 (list) 。

总结

图是一种很简单的数据结构。图的组织方式比较松散，自由度比较大，但也造成比较高的算法复杂度。我将在以后介绍一些图的经典算法。