混沌数学之Duffing(杜芬)振子
杜芬振子 Duffing oscillator是一个描写强迫振动的振动子,由非线性微分方程表示
杜芬方程列式如下:

其中
- γ控制阻尼度
- α控制韧度
- β控制动力的非线性度
- δ驱动力的振幅
- ω驱动力的圆频率
杜芬方程没有解析解,但可用龙格-库塔法求得数值解。
当γ>0,杜芬振子呈现极限环振动;
相关软件:混沌数学及其软件模拟
相关代码:
//http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.html?re=view
class DuffingEquation : public DifferentialEquation
{
public:
DuffingEquation()
{
m_StartX = 1.0f;
m_StartY = 1.0f;
m_StartZ = 0.0f; m_ParamA = 2.09f;
m_ParamB = 0.1f;
m_ParamC = 0.5f; m_StepT = 0.002f;
} void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ)
{
dX = y;
dY = m_ParamA*cosf(m_ParamC*m_ParamT) - m_ParamB*y + x - x*x*x;
dZ = 0.0f;
} bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
bool IsValidParamC() const {return true;}
bool IsValidParamT() const {return true;}
};
相关截图:
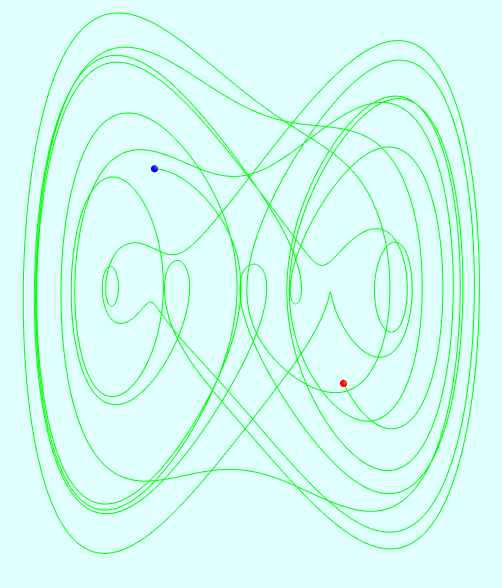
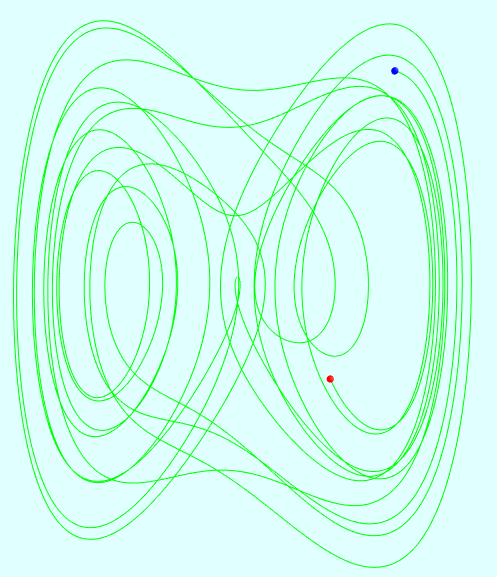



混沌数学之Duffing(杜芬)振子的更多相关文章
- 混沌数学之Lorenz(洛伦茨)吸引子
洛伦茨吸引子是洛伦茨振子(Lorenz oscillator)的长期行为对应的分形结构,以爱德华·诺顿·洛伦茨的姓氏命名. 洛伦茨振子是能产生混沌流的三维动力系统,是一种吸引子,以其双纽线形状而著称. ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 混沌数学之logistic模型
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率. 相关DEMO参见:混沌数学之离散点集图形DEMO ...
- 混沌数学之Henon吸引子
Henon吸引子是混沌与分形的著名例子. 相关软件:混沌数学及其软件模拟相关代码: // http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.ht ...
- 混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)
拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)是 1979年苏联物理学家拉比诺维奇和法布里康特提出模拟非平衡介 质自激波动的非线性常微分方程组: dot{x ...
- 混沌数学之Rössler(若斯叻)吸引子
若斯叻吸引子(Rössler attractor)是一组三元非线性微分方程: frac{dx(t)}{dt} = -y(t)-z(t) frac{dy(t)}{dt} = x(t)+a*y(t) fr ...
- 混沌数学之ASin模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: class ASinEquation : public DiscreteEquation { public: ASinEquation() { m ...
- 混沌数学之Kent模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: // http://wenku.baidu.com/view/7c6f4a000740be1e650e9a75.html // 肯特映射 clas ...
- 混沌数学之Feigenbaum模型
1975年,物理学家米切尔·费根鲍姆(Mitchell Feigenbaum)发现,一个可用实验加以测 量的特殊数与每个周期倍化级联相联系.这个数大约是4.669,它与π并列成为似乎在数学 ...
随机推荐
- shell变量定义中的特殊符号
今天要写一个shell语句来输出数据库的v$database的信息 定义bb为一个接收sql返回值的变量 需要注意的是: select * from v$database ; 语句 由于其中用到了$ ...
- spring boot上传文件错误The temporary upload location [/tmp/tomcat.5260880110861696164.8090/work/Tomcat/localhost/ROOT] is not valid
参考了:https://www.jianshu.com/p/cfbbc0bb0b84 再次感谢,但还是有些调整 一.在zuul服务中加入两个配置参数(location: /data/apps/temp ...
- MySQL服务器 IO 100%的案例分析
[问题] 有台MySQL 5.6.21的数据库实例以写入为主,IO %util接近100% 写入IOPS很高 [分析过程] 1.通过iotop工具可以看到当前IO消耗最高的mysql线程 2.查看线程 ...
- Web服务评估工具Nikto
Web服务评估工具Nikto Nikto是一款Perl语言编写的Web服务评估工具.该工具主要侧重于发现网站的默认配置和错误配置.它通过扫描的方式,检测服务器.服务和网站的配置文件,从中找出默认配 ...
- s3c2440地址分配
mini2440的地址怎么分配.mini2440处理器的地址怎么分配. S3C2440处理器可以使用的物理地址空间可以达到4GB,其中前1GB的地址为连接外设的地址空间.>1G的地址空间 分配给 ...
- 【set】【可持久化Trie】The 16th UESTC Programming Contest Preliminary K - Will the circle be broken
题意:You are given an array A of N non-negative integers and an integer M. Find the number of pair(i,j ...
- 【单调队列】BZOJ1342-[Baltic2007]Sound静音问题
[题目大意] 给出一个n个数的序列,以哪位位置为开头的长度为m的区间满足该区间的最大值与最小值的差≤一个定值. [思路] 单调队列……说一下单调队列比较方便的操作. 把第一个先丢进去,开始条件为hea ...
- MyBatis -- generator 逆向工程
一.引言 官网文档:http://www.mybatis.org/generator/index.html 通过使用官方提供的mapper自动生成工具,mybatis-generator-core-1 ...
- JBOSS集群和安装
JBOSS集群和安装 http://jijian91.com/blog20071010/jboss-cluster-part5.html http://wing123.iteye.com/blog/3 ...
- 216. 组合总和 III
216. 组合总和 III 题意 找出所有相加之和为 n 的 k 个数的组合.组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字. 说明: 所有数字都是正整数. 解集不能包含重复的 ...
