【论文笔记】Modeling User Exposure in Recommendation

Modeling User Exposure in Recommendation

【论文作者】Dawen Liang, David M. Blei, etc.

WWW’16 Columbia University

---

目录

• Modeling User Exposure in Recommendation
  • 0. 总结
  • 1.研究目标
  • 2.问题背景
  • 3. 方法
    • 3.1 模型描述
    • 3.2 对曝光概率的建模
    • 3.3 参数学习
    • 3.4 预测模型
  • 4. 实验
    • 4.1 数据集
    • 4.2 实验结果
    • 4.3模型分析
    • 4.4 加入内容信息的曝光模型
  • 疑问

0. 总结

这篇文章构建了曝光概率这个隐变量，用EM算法进行参数优化，并提出了基于流行度和基于内容的两种曝光概率参数模型。实验表明，提出的方法性能得到了较大提升。

1.研究目标

通过建模曝光概率，去除推荐系统中的exposure bias。

2.问题背景

在推荐系统场景下，显示反馈数据可以同时获得用户的正负反馈信息，但获取难度较大，相关数据较少。在隐式反馈数据中，所有未发生交互的user-item pairs都被视为负样本，但是用户没有与一个物品发生交互，有可能是因为用户真的不喜欢，也可能是因为用户不知道这个物品，这就是推荐系统当中的exposure bias。

3. 方法

3.1 模型描述

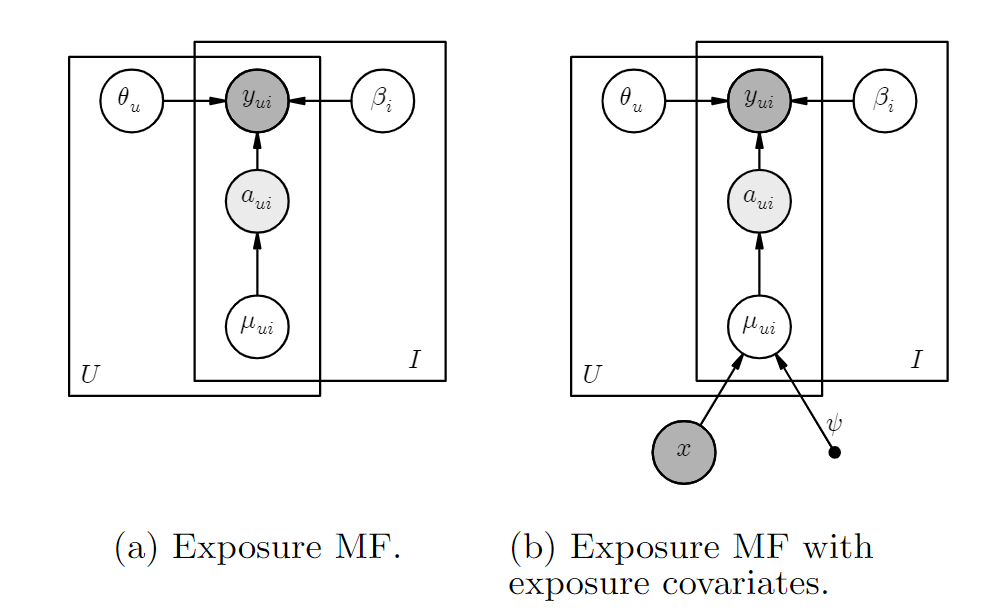
本文将曝光与否建模为隐变量\(a_{ui}\)，\(a_{ui}\)服从参数为\(\mu_{ui}\)的伯努利分布（0-1分布）。

u和i的embedding的各维度独立同分布，分别服从一个均值为0，方差为\(\lambda_{\theta}^{-1}\)的正态分布。

当\(a_{ui}=1\)时，\(y_{ui}\)服从均值为\(\boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}\)，方差为\(\lambda_{y}^{-1}\)的正态分布。

当\(a_{ui}=0\)时，表明i没有被u观测到，交互概率\(y_{ui}\)趋近于0。

\[\boldsymbol{\theta}_{u} \sim \mathcal{N}\left(\mathbf{0}, \lambda_{\theta}^{-1} I_{K}\right) \\
\boldsymbol{\beta}_{i} \sim \mathcal{N}\left(\mathbf{0}, \lambda_{\beta}^{-1} I_{K}\right) \\
a_{u i} \sim \operatorname{Bernoulli}\left(\mu_{u i}\right) \\
y_{u i} | a_{u i}=1 \sim \mathcal{N}\left(\boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right) \\
y_{u i} | a_{u i}=0 \sim \delta_{0},
\]

基于上述概率分布，可以推导出\(a_{ui}\)和\(y_{ui}\)的联合条件概率分布为

\[\begin{aligned}
&\log p \left(a_{u i}, y_{u i} | \mu_{u i}, \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right) \\ \\

= &\log \left[p\left(a_{ui}|\mu_{u i}, \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right) * p \left( y_{ui}|a_{ui}, \mu_{u i}, \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \lambda_{y}^{-1} \right)\right ]\\ \\

= &\log p\left(a_{ui}|\mu_{u i} \right) + \log p \left( y_{ui}|a_{ui}, \mu_{u i}, \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \lambda_{y}^{-1} \right) \\ \\

= & \log p\left(a_{ui}|\mu_{u i} \right) + \mathbb{I}\left[a_{u i}=1\right] \log p \left( y_{ui}|a_{ui}=1, \mu_{u i}, \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \lambda_{y}^{-1} \right) + \\

&\mathbb{I}\left[a_{u i}=0\right] \log p \left( y_{ui}|a_{ui}=0, \mu_{u i}, \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \lambda_{y}^{-1} \right)\\ \\

= &\log \operatorname{Bernoulli}\left(a_{u i} | \mu_{u i}\right)+a_{u i} \log \mathcal{N}\left(y_{u i} | \boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right) + \\

&\left(1-a_{u i}\right) \log \mathbb{I}\left[y_{u i}=0\right]
\end{aligned}
\]

当\(y_{ui} = 1\)时，\(a_{ui} = 1\)，因此我们只考虑\(y_{ui} = 0\)的情况。

当\(y_{ui} = 0\)时，若\(\boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}\)较大，则\(\mathcal{N}\left(y_{u i} = 0 | \boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right)\)较小，使得\(p(a_{ui} = 1,y_{ui} = 0)\)较小，迫使我们相信\(a_{ui} = 0\)。直观上讲，若一个物品符合用户兴趣（\(\boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}\)较大），且没有发生交互（\(y_{ui} = 0\)），则用户很可能是因为没有看到这个物品（\(a_{ui} = 0\)）。

3.2 对曝光概率的建模

• per item \(\mu_i\)：直接用物品流行度作为曝光参数\(\mu_{ui}\)的初始值，只使用点击数据，不使用额外信息，\(\mu_i \sim Beta(\alpha_1,\alpha_2)\)。
• 基于上下文的建模：首先基于提取物品的特征向量\(\boldsymbol{x_i}\)，并为每个user学习一个表示\(\boldsymbol{\psi_u}\)，则\(\mu_{ui} = \sigma(\psi_u^\top \boldsymbol{x_i})\)。

3.3 参数学习

由于模型中含有因变量\(a_{ui}\)，使用EM算法来学习模型参数。

• E-step：对于\(y_{ui} = 1\)的交互，\(a_{ui} = 1\)，不需要学习。对于\(y_{ui} = 0\)的交互：

\[\begin{aligned}
&\mathbb{E}\left[a_{u i} \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \mu_{u i}, y_{u i}=0\right]\\\\

= &\frac{p(a_{ui} = 1, y_{ui} = 0 \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \mu_{u i})}
{p(a_{ui} = 1, y_{ui} = 0 \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \mu_{u i}) +
p(a_{ui} = 0, y_{ui} = 0 \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \mu_{u i})} \\ \\

= &\frac{p(a_{ui} = 1) \cdot p(y_{ui} = 0 \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, a_{ui} = 1)}
{p(a_{ui} = 1) \cdot p(y_{ui} = 0 \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, a_{ui} = 1) +
p(a_{ui} = 0 \mid \mu_{ui})} \\ \\

=&\frac{\mu_{u i} \cdot \mathcal{N}\left(0 \mid \boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right)}

{\mu_{u i} \cdot \mathcal{N}\left(0 \mid \boldsymbol{\theta}_{u}^{\top} \boldsymbol{\beta}_{i}, \lambda_{y}^{-1}\right)+\left(1-\mu_{u i}\right)}
\end{aligned}
\]

• M-step：

为简化表达，令\(p_{ui} = \mathbb{E}\left[a_{u i} \mid \boldsymbol{\theta}_{u}, \boldsymbol{\beta}_{i}, \mu_{u i}, y_{u i}=0\right]\)，则：

\[\begin{aligned}
&\boldsymbol{\theta}_{u} \leftarrow\left(\lambda_{y} \sum_{i} p_{u i} \boldsymbol{\beta}_{i} \boldsymbol{\beta}_{i}^{\top}+\lambda_{\theta} I_{K}\right)^{-1}\left(\sum_{i} \lambda_{y} p_{u i} y_{u i} \boldsymbol{\beta}_{i}\right) \\ \\
&\boldsymbol{\beta}_{i} \leftarrow\left(\lambda_{y} \sum_{u} p_{u i} \boldsymbol{\theta}_{u} \boldsymbol{\theta}_{u}^{\top}+\lambda_{\beta} I_{K}\right)^{-1}\left(\sum_{u} \lambda_{y} p_{u i} y_{u i} \boldsymbol{\theta}_{u}\right)
\end{aligned}
\]

曝光先验概率\(\mu_{ui}\)的优化：

• per-item \(\mu_{ui}\)

  由于\(\mu_{i}\)服从beta分布，即\(\mu_{i} \sim Beta(\alpha_1 + \sum_u p_{ui}, \alpha_2 + U - \sum_u p_{ui})\)，则

  \[\mu_{i} \leftarrow \frac{\alpha_{1}+\sum_{u} p_{u i}-1}{\alpha_{1}+\alpha_{2}+U-2}
  \]

• 基于上下文的先验概率\(\mu_{ui}\)

  也就是用E-step生成的\(p_{ui}\)来监督\(\mu_{ui}\)

  \[\psi_{u}^{\text {new}} \leftarrow \psi_{u}+ \eta \nabla_{\psi_{u}}\mathcal{L}
  \]

\[\nabla_{\boldsymbol{\psi}_{u}} \mathcal{L}=\frac{1}{I} \sum_{i}\left(p_{u i}-\sigma\left(\boldsymbol{\psi}_{u}^{\top} \mathbf{x}_{i}\right)\right) \mathbf{x}_{i}
\]

​ 实现时，对每个user，不计算与所有item的交互，而是随机采样一些item，以降低计算复杂度。

3.4 预测模型

预测时，可以用\(\hat{y}_{ui} = \mu_{ui} \cdot \boldsymbol{\theta_u^\top\beta_i}\)，也可以直接用\(\hat{y}_{ui} = \theta_u^\top\beta_i\)。在本文的实验中，如果采用per-item exposure model，则后者好；如果曝光先验概率模型中加入了item的物品信息，则前者好。

可能是因为加入了item信息的曝光模型对曝光概率的预测更准确，因此在预测时加入\(\mu_{ui}\)效果更好。

4. 实验

4.1 数据集

\[\begin{array}{ccccc}
\hline & \text { TPS } & \text { Mendeley } & \text { Gowalla } & \text { ArXiv } \\
\hline \text { # of users } & 221,830 & 45,293 & 57,629 & 37,893 \\
\text { # of items } & 22,781 & 76,237 & 47,198 & 44,715 \\
\text { # interactions } & 14.0 \mathrm{M} & 2.4 \mathrm{M} & 2.3 \mathrm{M} & 2.5 \mathrm{M} \\
\% \text { interactions } & 0.29 \% & 0.07 \% & 0.09 \% & 0.15 \% \\
\hline
\end{array}
\]

4.2 实验结果

\[\begin{array}{c|cc|cc|cc|cc}
& {\text { TPS }} & & {\text { Mendeley }} & & {\text { Gowalla }}& & {\text { ArXiv }} \\
\hline & \text { WMF } & \text { ExpoMF } & \text { WMF } & \text { ExpoMF } & \text { WMF } & \text { ExpoMF } & \text { WMF } & \text { ExpoMF } \\
\hline \text { Recall@20 } & 0.195 & \mathbf{0 . 2 0 1} & 0.128 & \mathbf{0 . 1 3 9} & \mathbf{0 . 1 2 2} & 0.118 & 0.143 & \mathbf{0 . 1 4 7} \\
\text { Recall@50 } & \mathbf{0 . 2 9 3} & 0.286 & 0.210 & \mathbf{0 . 2 2 1} & \mathbf{0 . 1 9 2} & 0.186 & \mathbf{0 . 2 3 7} & 0.236 \\
\text { NDCG@100 } & 0.255 & \mathbf{0 . 2 6 3} & 0.149 & \mathbf{0 . 1 5 9} & \mathbf{0 . 1 1 8} & 0.116 & 0.154 & \mathbf{0 . 1 5 7} \\
\text { MAP@100 } & 0.092 & \mathbf{0 . 1 0 9} & 0.048 & \mathbf{0 . 0 5 5} & \mathbf{0 . 0 4 4} & 0.043 & 0.051 & \mathbf{0 . 0 5 4}
\end{array}
\]

4.3模型分析

从结果上，对于未点击的物品，如果用户感兴趣的概率较高，则该物品被曝光的概率应该比较低。

从训练过程上看，模型中的曝光变量使得MF模型能够专注于曝光概率高的user-item pairs。

图中，横坐标表示物品流行度，红色虚线表示学到的per-item先验曝光概率，蓝色点表示后验曝光概率。画出的点都是没有发生过交互的。

在User A的图中，方框框出的点表示跟用户兴趣比较相符的物品，但是没有发生交互，模型可以将对应的曝光概率降低。也就是说，用户更可能是因为没有看到这个物品而没有发生交互，而不是因为不感兴趣。

在User B的图中，方框框出了流行度最高的两个物品（流行度非常接近），但是其中一个物品更接近用户兴趣，模型得出的响应曝光概率明显低于另一个物品。

4.4 加入内容信息的曝光模型

曝光参数模型：

\[\mu_{ui} = \sigma(\psi_u^\top \bold{x_i} + \gamma_u)
\]

物品特征提取方式：

• Mendeley：共K个文章类别，使用LDA模型，通过内容信息，得到文章属于每个类别的概率，从而为每个item生成一个特征向量。
• Gowalla：使用K-means得到K个聚类中心，计算每个位置与K个中心的距离，得到一个特征向量。

训练结果（第二行的两个图）：

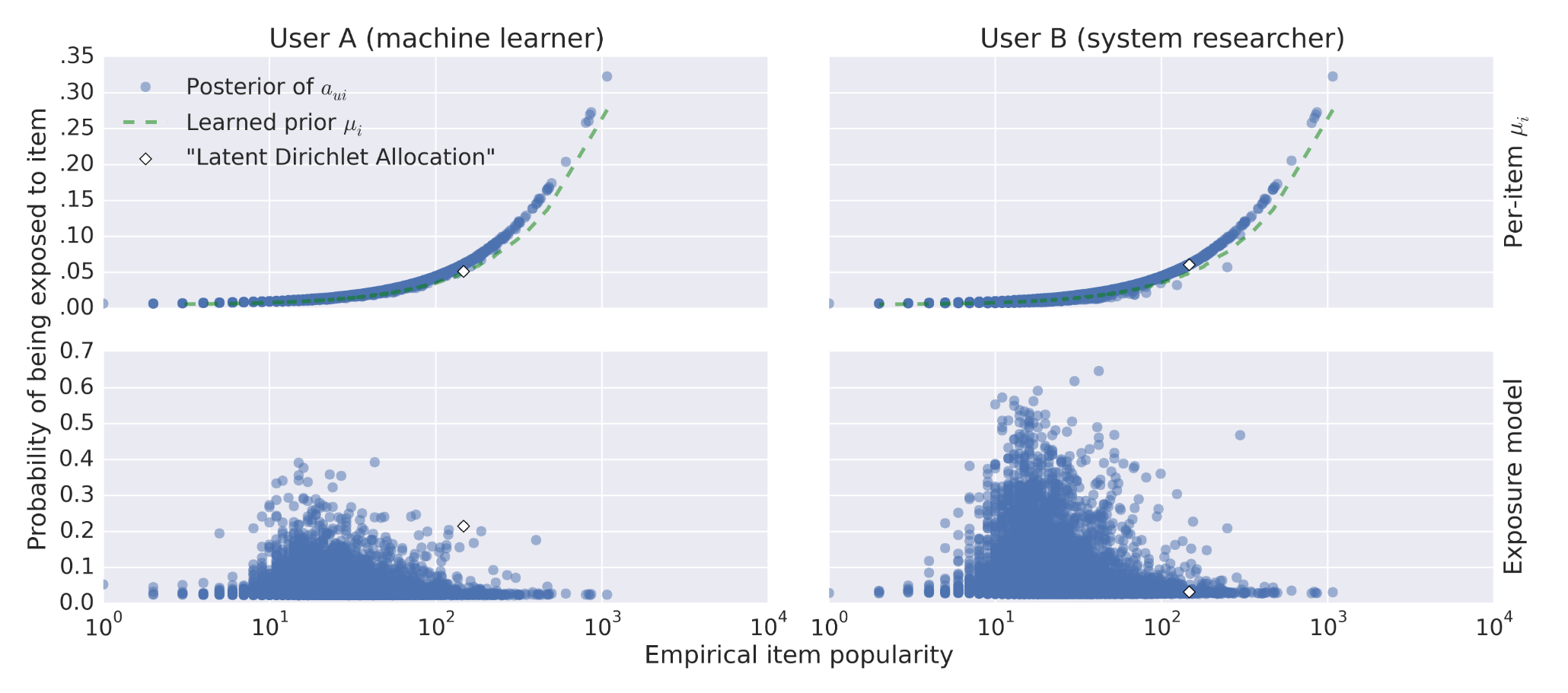
加入内容信息之后，曝光概率与流行度的相关性大大降低，模型性能也得到了较大提升。

\[\begin{array}{cccc}
\hline & \text { WMF } & \text { ExpoMF } & \text { Location ExpoMF } \\
\hline \text { Recall@20 } & 0.122 & 0.118 & \mathbf{0 . 1 2 9} \\
\text { Recall@50 } & 0.192 & 0.186 & \mathbf{0 . 1 9 9} \\
\text { NDCG@100 } & 0.118 & 0.116 & \mathbf{0 . 1 2 5} \\
\text { MAP@100 } & 0.044 & 0.043 & \mathbf{0 . 0 4 8} \\
\hline
\end{array}
\]

疑问

3.3 M-step不理解