B树和B+树原理图文解析

B树与B+树不同的地方在于插入是从底向上进行（当然查找与二叉树相同，都是从上往下）

二者都通常用于数据库和操作系统的文件系统中，非关系型数据库索引如mongoDB用的B树，大部分关系型数据库索引使用的是B+树。

一、B树（也叫B-树，注意并不是读B减树哦）

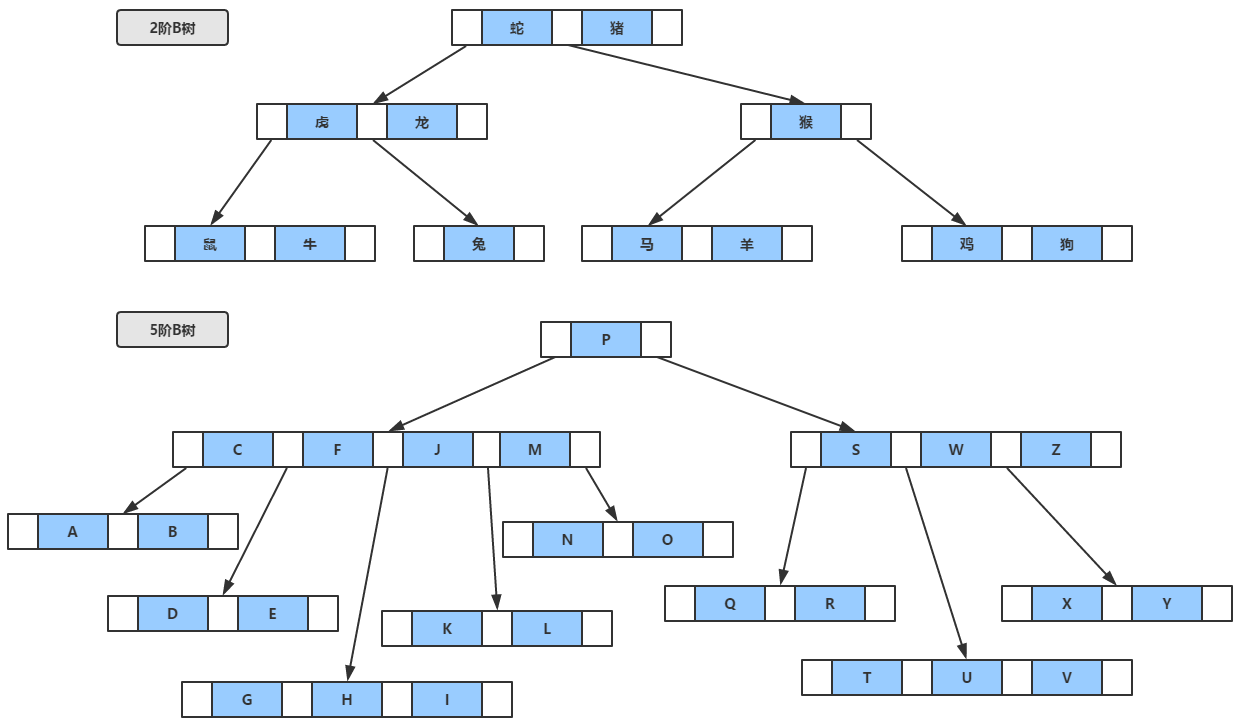
m阶B树需满足以下要求：

1、m阶B树：m阶指的是分叉的个数最多为m个。即一个非叶子节点最多可以有m个子节点。

2、子节点：一个叉连接的表示一个子节点，如果所示CFJM 表示一个子节点，其中CFJM表示4个元素。一个非叶子节点可以表示为[A0 k1 A1 k2 A2……kn An]，其中ceil(m/2) -1 <= k <= m-1个，因此ceil(m/2) <= A <= m，A表示指向子节点的指针。

3、根节点至少有两个子节点。

4、所有的叶子在同一层。

上图所示并未画出叶子节点，因为叶子结点不包含元素，所以可以把叶子结点看成在树里实际上并不存在外部结点，指向这些外部结点的指针为空，叶子结点的数目正好等于树中所包含的元素总个数加1。下图画出了叶子节点。

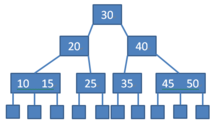
B树的特点可以总结为如下：

1. 元素集合分布在整颗树中。
2. 任何一个元素出现且只出现在一个节点中。
3. 搜索有可能在非叶子节点结束。
4. 因为每个节点中的元素和子树都是有序的，其搜索性能等价于在元素集合内做一次二分查找。
5. B树在插入删除新的数据记录会破坏B-Tree的性质，因为在插入删除时，需要对树进行一个分裂、合并、转移等操作以保持B-Tree性质。

为什么要使用B-树作为数据库索引而不是使用二叉树？

二叉树的搜索效率是十分高的，可以达到logN,但是由于数据量巨大时，索引的大小甚至可以达到G级别，所以索引是存储在磁盘中的，每次查找只能逐一将索引树的节点加载至内存中，如果使用二叉树则I/O操作将会非常频繁，I/O次数取决于二叉树的深度。这样索引速度非常慢，因此采用B树这种多路二叉搜索树大大减少I/O次数。其中多路指的是一个节点有多个子树，并且由于所有叶子节点都在同一层，因此是平衡树。

磁盘页：查询索引时，逐一加载磁盘页，这里的磁盘页对应索引树的节点，对于m阶B树，m的大小取决于磁盘页的大小。

 B+树

m阶B树具有以下几个特征：

1、有k个子树的中间节点包含有k个元素（B树中是k-1个），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点中。

2、所有的叶子结点中包含了全部元素的信息，叶子节点本身根据元素的大小顺序链接。

3、所有的中间节点元素都同时存在子节点，在子节点元素中是最大（或最小）元素。

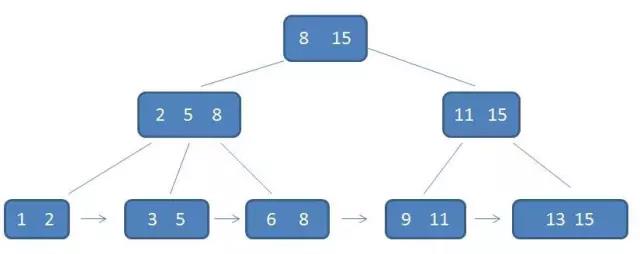
对于根节点中的8，在其子节点中 2 5 8中是最大元素，根节点的最大元素15也是整棵树的最大元素。

什么是卫星数据？

索引元素所指向的数据记录，比如数据库中的某一行。

在B树中无论是中间节点还是叶子节点都带有卫星数据，但是在B+树中只有叶子节点带有卫星数据，中间节点仅仅是索引。左图是B树，右图是B+树。

      

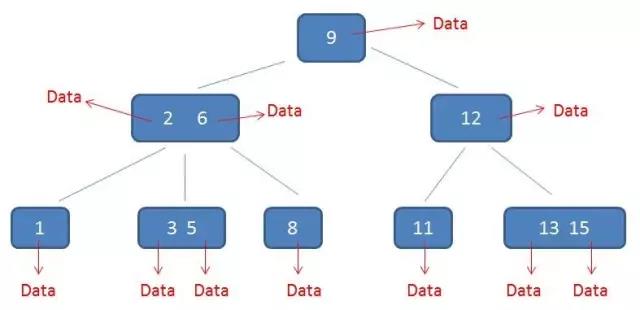
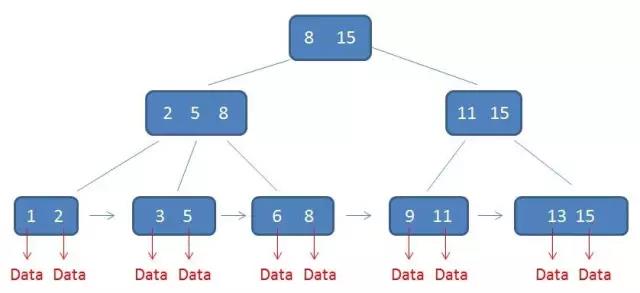
相比B树B+树有以下几点优点：

（1）由于B+树的中间节点没有卫星数据，因此同样大小的磁盘页可以容纳更多的节点元素，即B+树相比B树更加矮胖，因此查询时的I/O次数更少。

（2）由于B树在查找时最好情况是根节点，最差情况是叶子节点；B+树都是查找到叶子节点，所以B+树的查找更加稳定。

（3）对于范围查找，例如查找3-11之间的所有数据，对于B树，查找下限3，然后中序遍历；对于B+树只需要在叶节点链表上遍历即可，范围查找的效率更高。

 数据库中的聚集索引中，叶子节点直接包含卫星数据，在非聚集索引中，叶子节点带有指向卫星数据的指针。