[PROC FREQ] 单组率置信区间的计算

本文链接：https://www.cnblogs.com/snoopy1866/p/15674999.html

利用PROC FREQ过程中的binomial语句可以很方便地计算单组率置信区间，SAS提供了9种（不包括校正法）计算单组率置信区间的方法，现列举如下：

首先准备示例数据：

data test;
    input out $ weight;
cards;
阳性 95
阴性 5
;
run;

1. Wald 法

基于Wald法构建的单组率的置信区间应用非常广泛，且Wald在结构上有着以点估计为中心对称分布的天然优势，基于Wald法构建的单样本率置信区间可表示为：

\[p\pm z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}
\]

优点：以点估计为中心，对称分布

缺点：（1）Overshoot: 置信区间可能超过[0,1]范围（2）Degeneracy: 区间宽度可能为0（p=0或1时）（3）覆盖率差

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = wald);
    weight weight;
run;

2. Wald 法（连续性校正）

\[p\pm \left( z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} + \frac{1}{2n} \right)
\]

优点：（1）可避免区间宽度可能为0的情况（2）覆盖率较Wald法有所改善

缺点：（1）结果偏保守（2）更容易发生置信区间超过[0,1]范围的情况

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = wald(correct));
    weight weight;
run;

3. Agresti-Coull

Agresti-Coull法的主要思路是选择一个大于0的常数作为pseudo-frequency，在计算样本量的时候对点估计进行校正，目的是使点估计尽量向中央（0.5）靠拢，这个大于零0的常数被称为估计因子\(\phi\)。

Agresti和Coull提出了\(\phi\)的两种形式，\(\phi =\frac{1}{2}z_{\alpha/2}^2\)和\(\phi = 2\)，前者称为ADDZ2校正法，后者称为ADD4校正法，SAS中仅提供ADDZ2校正法，当\(\alpha = 0.05\)时，\(z_{\alpha/2}\)接近2，此时ADDZ2校正法与ADD4校正法近似。

当\(\phi = 2\)时（ADD4校正法），其实际含义是样本成功率和失败例数分别加2，即总样本量加4。

\[\tilde{p} \pm \sqrt{\frac{\tilde{p}(1-\tilde{p})}{n + z_{\alpha/2}^2}}
\]

其中\(\tilde{p} = \frac{n_1 + \frac{1}{2}z_{\alpha/2}^2}{n + z_{\alpha/2}^2}\)

优点：（1）downward spikes现象略有改善（downward spikes：当率在极端情况下，置信区间覆盖率急剧下滑）

缺点：（1）牺牲了置信区间宽度

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = agresticoull);
    weight weight;
run;

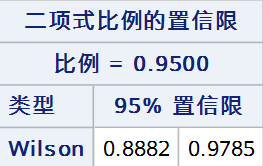
4. Wilson Score法

Wilson Score法作为Wald法的替代，应用十分广泛，是目前学界公认的在非极端率情况下的最佳置信区间构建方法。

基于Wilson Score法构建的置信区间可表示为：

\[\left\vert p-\hat{p} \right\vert = z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}
\]

\(p\)可表示为：

\[\frac{1}{1 + \frac{1}{n}z_{\alpha/2}^2}
\left( \hat{p} + \frac{z_{\alpha/2}^2}{2n} \pm z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p}) + \frac{1}{4n}z_{\alpha/2}^2}{n}} \right)
\]

优点：（1）被认为是moderate proportion（率不接近0或1）的最佳方法

缺点：（1）存在downward spikes现象

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = wilson);
    weight weight;
run;

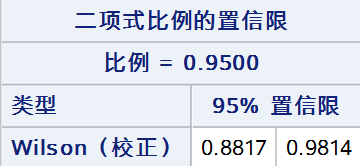
5. Wilson Score法（连续性校正）

基于Wilson Score法连续性校正构建的置信区间可表示为：

\[\left\vert p-\hat{p} \right\vert - \frac{1}{2n} = z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}
\]

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = wilson(correct));
    weight weight;
run;

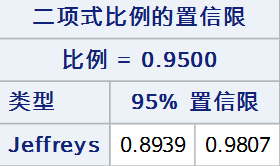
6. Jeffreys法

Jeffreys法构建的置信区间表示如下：

\[L={\rm Beta}\left( \frac{\alpha}{2}, n_1 + \frac{1}{2}, n - n_1 + \frac{1}{2} \right)
\]

\[U={\rm Beta}\left( 1 - \frac{\alpha}{2}, n_1 + \frac{1}{2}, n - n_1 + \frac{1}{2} \right)
\]

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = jeffreys);
    weight weight;
run;

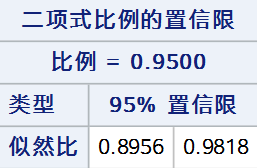
7. 似然比法

似然比法通过逆推似然比检验构造置信区间，零假设下似然比检验统计量可表示为：

\[L(p_0) = -2\left( n_1\ln{\frac{\hat{p}}{p_0}} + (n - n_1)\ln{\frac{1 - \hat{p}}{1 - p_0}} \right)
\]

使检验统计量\(L(p_0)\)落在接受域内的所有\(p_0\)组成的区间即为似然比法的置信区间：\(\{p_0: L(p_0) < \chi_{1,\alpha}^2\}\)，PROC FREQ通过迭代计算寻找置信限。

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = likelihoodratio);
    weight weight;
run;

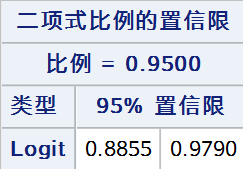
8. Logit法

基于Logit变换 \(Y = \ln(\frac{\hat{p}}{1 - \hat{p}})\)，\(Y\) 的近似置信区间用以下公式计算：

\[Y_L = \ln{\frac{\hat{p}}{1 - \hat{p}}} - z_{\alpha /2} \sqrt{\frac{n}{n_1(n - n_1)}}
\]

\[Y_U = \ln{\frac{\hat{p}}{1 - \hat{p}}} + z_{\alpha /2} \sqrt{\frac{n}{n_1(n - n_1)}}
\]

\(p\) 的置信区间可表示为：

\[P_L = \exp{\left( \frac{Y_L}{1 + \exp{(Y_L)}} \right)}
\]

\[P_U = \exp{\left( \frac{Y_U}{1 + \exp{(Y_U)}} \right)}
\]

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = likelihoodratio);
    weight weight;
run;

9. Clopper-Pearson法

基于二项分布构建的置信区间方法，使得精确置信限满足以下方程：

\[\sum_{x = n_1}^n \dbinom{n}{x} P_L^x(1 - P_L)^{n - x} = \frac{\alpha}{2}
\]

\[\sum_{x = 0}^{n_1} \dbinom{n}{x} P_U^x(1 - P_U)^{n - x} = \frac{\alpha}{2}
\]

PROC FREQ 使用 \(F\) 分布计算Clopper-Pearson置信限，公式如下：

\[P_L = \left[ 1 + \frac{n - n_1 + 1}{n_1 F\left( \frac{\alpha}{2}, 2n_1, 2(n - n_1 + 1) \right)} \right]^{-1}
\]

\[P_U = \left[ 1 + \frac{n - n_1}{(n_1 + 1) F\left( 1 - \frac{\alpha}{2}, 2(n_1 + 1), 2(n - n_1) \right)} \right]^{-1}
\]

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = likelihoodratio);
    weight weight;
run;

10. Mid-P法

Mid-P 精确置信限满足以下方程：

\[\sum_{x = n_1 + 1}^n \dbinom{n}{x} P_L^x(1 - P_L)^{n-x} + \frac{1}{2}\dbinom{n}{n_1} P_L^{n_1}(1-P_L)^{n-n_1} = \frac{\alpha}{2}
\]

\[\sum_{x = 0}^{n_1 - 1} \dbinom{n}{x} P_U^x(1 - P_U)^{n-x} + \frac{1}{2}\dbinom{n}{n_1} P_U^{n_1}(1-P_U)^{n-n_1} = \frac{\alpha}{2}
\]

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = midp);
    weight weight;
run;

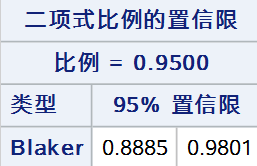
11. Blaker法

通过对双侧 Blaker 精确检验逆推来构建置信区间，使检验统计量\(B(p_0, n_1)\)落在接受域内的所有\(p_0\)组成的区间称为Blaker置信区间：\(\{ p_0: B(p_0, n_1) > \alpha \}\)

其中：

\[B(p_0, n_1) = {\rm Prob}\left( \gamma(p_0, X) \le \gamma(p_0, n_1)|p_0 \right)
\]

\[\gamma(p_0, n_1) = \min{\left( {\rm Prob}(X \ge n_1|p_0), {\rm Prob}(X \le n_1|p_0) \right)}
\]

代码：

proc freq data = test;
    tables out /nopercent nocol norow nocum binomial(level = "阳性" cl = blaker);
    weight weight;
run;

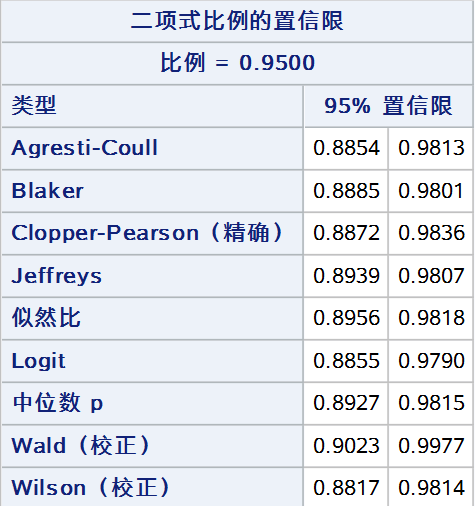
最后，将以上9种方法同时展示（wald 和 wilson 仅展示校正法）：

proc freq data = test;
    tables out /nopercent nocol norow
                nocum binomial(level = "阳性"
                               cl = (wald(correct)  agresticoull    wilson(correct)
                                     jeffreys       likelihoodratio logit
                                     clopperpearson midp            blaker));
    weight weight;
run;

参考文献：徐莹. 一种新的单样本率的置信区间估计方法[D].南方医科大学,2019.