图论---最小生成树----普利姆(Prim)算法

普利姆(Prim)算法

1. 最小生成树（又名：最小权重生成树）

概念：将给出的所有点连接起来（即从一个点可到任意一个点），且连接路径之和最小的图叫最小生成树。最小生成树属于一种树形结构（树形结构是一种特殊的图），或者说是直链型结构，因为当n个点相连，且路径和最短，那么将它们相连的路一定是n-1条。

可以利用参考一个问题理解最小生成树，有n个村庄，每个村庄之间距离不同，要求村庄之间修路，每一个村庄必须与任意一个村庄联通，如何修路最省钱（修的最短）。

2. 普利姆算法介绍

利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有(n-1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图

具体过程如下：

(1)设G=(V,E)是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合

(2)若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的visited[u]=1

(3)若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj加入集合U中，将边（ui,vj）加入集合D中，标记visited[vj]=1

(4)重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有n-1条边

3.图例描述

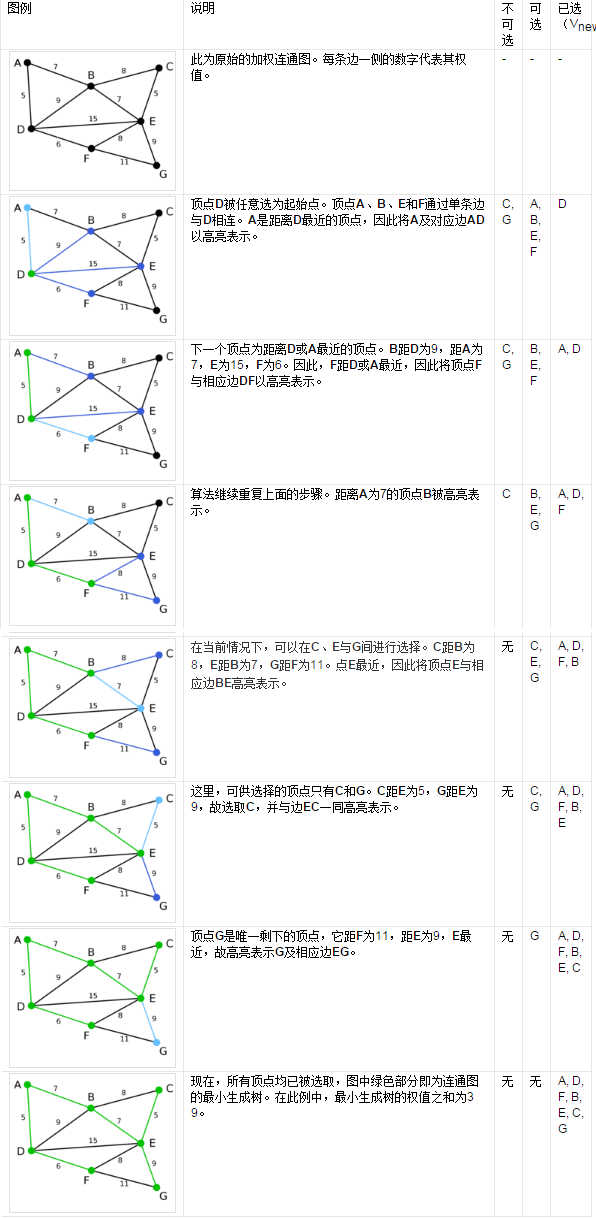
4.Prime代码

#include <stdio.h>
#include <stdlib.h>
#include<iostream>
using namespace std;

#define n 20
#define MaxNum 10000  /*定义一个最大整数*/

/*定义邻接矩阵类型*/
typedef int adjmatrix[n + 1][n + 1];
typedef struct {
    int fromvex, tovex;                 //生成树的起点和终点
    int weight;                         //边的权重
} Edge;
typedef Edge *EdgeNode;                 //定义生成树的别名
int arcnum;     /*边的个数*/

/*建立图的邻接矩阵*/
void CreatMatrix(adjmatrix GA) {
    int i, j, k, e;
    cout<<"============================="<<endl;
    cout<<"图中有"<<n<<"个顶点 "<<endl;
    for(i=1; i<=n; i++) {
        for(j=1; j<=n; j++) {
            if(i==j) {
                GA[i][j]=0;         /*对角线的值置为0*/
            } else {
                GA[i][j]=MaxNum;    /*其他位置的值置初始化为一个最大整数*/
            }
        }
    }
    cout<<"请输入边的个数"<<endl;
    cin>>arcnum;
    cout<<"请输入边的信息，依照起点，终点，权值的形式输入："<<endl;
    for(k=1; k<=arcnum; k++) {
        cin>>i>>j>>e; /*读入边的信息*/
        GA[i][j]=e;
        GA[j][i]=e;
    }
}

/*初始化图的边集数组*/
void InitEdge(EdgeNode GE,int m) {
    int i;
    for(i=1; i<=m; i++) {
        GE[i].weight=0;
    }
}

/*依据图的邻接矩阵生成图的边集数组*/
void GetEdgeSet(adjmatrix GA,EdgeNode GE) {
    int i, j, k = 1;
    for(i=1; i<=n; i++) {
        for(j=i+1; j<=n; j++) {
            if(GA[i][j] !=0 && GA[i][j] != MaxNum) {
                GE[k].fromvex = i;
                GE[k].tovex = j;
                GE[k].weight = GA[i][j];
                k++;
            }
        }
    }
}

/*按升序排列图的边集数组*/
void SortEdge(EdgeNode GE,int m) {
    int i,j,k;
    Edge temp;
    for(i=1; i<m; i++) {
        k=i;
        for(j=i+1; j<=m; j++) {
            if(GE[k].weight > GE[j].weight) {
                k=j;
            }
        }
        if(k!=i) {
            temp = GE[i];
            GE[i]=GE[k];
            GE[k]=temp;
        }
    }
}

/*利用普里姆算法从初始点v出发求邻接矩阵表示的图的最小生成树*/
void Prim(adjmatrix GA,EdgeNode T) {
    int i,j,k,min,u,m,w;
    Edge temp;
    /*给T赋初值。相应为v1依次到其余各顶点的边*/
    k=1;
    for(i=1; i<=n; i++) {
        if(i!=1) {
            T[k].fromvex=1;
            T[k].tovex=i;
            T[k].weight=GA[1][i];
            k++;
        }
    }
    /*进行n-1次循环，每次求出最小生成树中的第k条边*/
    for(k=1; k<n; k++) {
        min=MaxNum;
        m=k;
        for(j=k; j<n; j++) {
            if(T[j].weight<min) {
                min=T[j].weight;
                m=j;
            }
        }
        /*把最短边对调到k-1下标位置*/ //可用swap替换
        temp=T[k];
        T[k]=T[m];
        T[m]=temp;
        /*把新增加最小生成树T中的顶点序号赋给j*/
        j=T[k].tovex;
        /*改动有关边，使T中到T外的每个顶点保持一条到眼下为止最短的边*/
        for(i=k+1; i<n; i++) {
            u=T[i].tovex;
            w=GA[j][u];
            if(w<T[i].weight) {
                T[i].weight=w;
                T[i].fromvex=j;
            }
        }
    }
}

/*输出边集数组的每条边*/
void OutEdge(EdgeNode GE,int e) {
    int i;
    printf("依照起点，终点。权值的形式输出的最小生成树为：\n");
    for(i=1; i<=e; i++) {
        printf("%d,%d,%d\n",GE[i].fromvex,GE[i].tovex,GE[i].weight);
    }
    printf("=============================\n");
}

int main() {
    adjmatrix GA;
    Edge GE[n*(n-1)/2], T[n];
    CreatMatrix(GA);
    InitEdge(GE,arcnum);
    GetEdgeSet(GA,GE);
    SortEdge(GE,arcnum);
    Prim(GA,T);
    printf("\n");
    OutEdge(T,n-1);
    return 0;
}