题解 [SDOI2009]E&D/染色游戏/Moving Pebbles

E&D

染色游戏

Moving Pebbles

E&D

题目大意

给出 \(2n\) 堆石子，\(2i-1\) 和 \(2i\) 为一组。每次可以选择一组删掉其中一堆，然后从同一组另外一堆选出若干石子放入被删掉的堆内，需要保证每个时刻每堆石子大小 \(\ge 1\)。不能操作的人就算输。问先手是否有必胜策略。

\(n\le 10^4\)

思路

首先我们发现我们肯定是对一组找出 sg 值，然后异或起来，于是问题就是如何求出 \(sg(x,y)\)，然后我们打表之后发现：

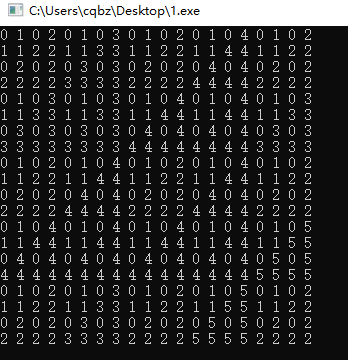
然后你通过 oies 发现 \(sg(n,m)\) 等于 \((n-1)|(m-1)\) 二进制下第一位为 0 的编号。

\(\texttt{Code}\)

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define MAXN 20005

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> void read (T &x,Args& ... args){read (x),read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int t,n,val[MAXN];

int fuckSG (int n,int m){
	if (n % 2 && m % 2) return 0;
	int sum = (n - 1) | (m - 1);
	for (Int i = 0;;++ i) if (!(sum >> i & 1)) return i;
}

signed main(){
	read (t);
	while (t --> 0){
		read (n);int sum = 0;
		for (Int i = 1;i <= n / 2;++ i){
			read (val[i * 2 - 1],val[i * 2]);
			sum ^= fuckSG (val[i * 2 - 1],val[i * 2]);
		}
		puts (sum ? "YES" : "NO");
	}
	return 0;
}

染色游戏

题目大意

一个 \(n\times n\) 的棋盘， 每次可以选择一个连通块，并把其中的硬币全部翻转，但是需要满足存在一个 硬币属于这个连通块并且所有其他硬币都在它的左上方(可以正左方也可以正 上方)，并且这个硬币是从反面向上翻成正面向上。dongdong 和 xixi 轮流操作。如果某一方无法操作，那么 ta 就输了。dongdong 先进行第一步操作，假设双方都采用最优策略。问 dongdong 是否有必胜策略。

\(n\le 100\)

思路

首先考虑一维的翻石子游戏，我们有定理：

局面的 sg 值为每个正面朝上的硬币的 sg 函数 nim 和

于是问题就是如何求出 \(sg(n,m)\)，然后你打表后发现：

\[sg(n,m)=\left\{\begin{array}{l}\text{lowbit}(n+m-1),n=1\vee m=1\\2^{n+m-2},\text{otherwise}\end{array}\right.
\]

\(\texttt{Code}\)

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define MAXN 205

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> void read (T &x,Args& ... args){read (x),read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int t,n,m;
bool f[205];
char s[MAXN];
int lowbit (int a){return a & (-a);}
int SG (int a,int b){
	if (a == 1 || b == 1) return (int)log2 (lowbit (a + b - 1));
	else return a + b - 2;
} 

signed main(){
	read (t);
	while (t --> 0){
		read (n,m);
		memset (f,0,sizeof (f));
		for (Int i = 1;i <= n;++ i){
			scanf ("%s",s + 1);
			for (Int j = 1;j <= m;++ j) if (s[j] != 'H') f[SG (i,j)] ^= 1;
		}
		int sum = 0;
		for (Int i = 0;i <= 200;++ i) sum |= f[i];
		puts (!sum ? "=_=" : "-_-");
	}
	return 0;
}

Moving Pebbles

题目大意

给出 \(n\) 堆石子，每次可以选择一堆石头，拿掉其中至少一个，然后可以移动若干个石子到任意一个石子堆内。

\(n\le 10^5\)

思路

这个题目有2个结论：

1. 当 \(n\) 为奇数时先手必胜

2. 当 \(n\) 为偶数时当且仅当每种石子堆数出现偶数次先手必败，否则先手必胜

首先我们可以清楚：当只有两堆且两堆石子数相同时，先手必败。因为后手可以做对称操作。然后结论 1 其实可以举个例子，当 \(n=3\) 时，因为我只要让后手遇见 2 堆相同情况即可。然后你发现删掉删掉最大堆一定可以做到。然后推广一下你就发现 \(n\) 为奇数的时候都可以做到。

结论 2 是因为奇数堆必胜，那当前为偶数堆的时候一定想让对手取完第一堆。这种时候当且仅当所有堆数都为 1 的情况出现。那么说白了就是一个 nim 博弈，如果满足每种石子堆数出现偶数那么 nim 和就为 0，先手必败，反之先手必胜。

感觉这个题还是很妙的，只是校内 OJ 数据水了一点导致很多人都过了。

\(\texttt{Code}\)

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define MAXN 100005

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> void read (T &x,Args& ... args){read (x),read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int n,a[MAXN];

signed main(){
	read (n);
	for (Int i = 1;i <= n;++ i) read (a[i]);
	if (n & 1){
		puts ("first player");
		return 0;
	}
	else{
		sort (a + 1,a + n + 1);
		for (Int i = 1;i <= n;i += 2)
			if (a[i] != a[i + 1]){
				puts ("first player");
				return 0;
			}
		puts ("second player");
	}
	return 0;
}