【CF632F】Magic Matrix(生成树 脑洞)

题目链接

大意

给定一个\(N\times N\)的矩阵，问是否满足以下三个条件：

1. \(A_{i,i}=0\)
2. \(A_{i,j}=A_{j,i}\)
3. 对于任意的\(i,j,k\)，满足\(A_{i,j}\ge max(A_{i,k},A_{k,j})\)

如果满足条件输出MAGIC，否则输出NOT MAGIC。

思路

首先，对于第一二两个条件，直接判就行了。

考虑第三个条件：

对于这个矩形，有个直观的想法就是建成一个完全图。

点\(i\)和点\(j\)间的边权就是\(A_{i,j}\)，那么第三个条件就转化为了：

对于任意一个三元环的三条边\(A,B,C\)



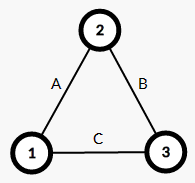
就有以下式子：

\[\begin{cases}
A\ge max(B,C)\\
B\ge max(A,C)\\
C\ge max(A,B)
\end{cases}
\]

化简一下即为，\(A,B,C\)中的最大值等于\(A,B,C\)中的次大值。

考虑如何快速地判断每一个三元环：

我们从小到大加边，权值相同的边一起加入，那么在任意时刻，图像中的每个连通块一定都是一个完全图，否则就不满足条件。

• 证明： 若图中的某个连通块不是一个完全图，那么一定会缺少一些边，形成如下图的例子：
  
  
  
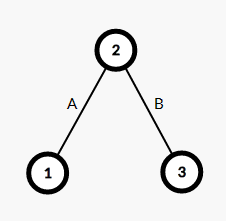
  而又由于1,3之间的边一定会严格大于\(A,B\)，则该三元环的最大值不等于次大值，即不满足上述条件。

对于判断加边后是否每个连通块都是完全图，我们可以用最小生成树的思想来做：

我们知道加完所有边后的图像是一个完全图，那么我们在加边时只用判断一下该边连接的两个点是否在同一连通块内就行了。如果在同一连通块内，就说明之前形成了一个缺边的非完全图，就直接不合法了。

注：权值相同的边一定要一起加入呀。

代码

其实一个就是Kruskal算法。

#include<map>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN=2505;
int N,A[MAXN][MAXN],Len;
int Fa[MAXN],B[MAXN*MAXN],Cnt,NCnt;
struct Edge{int x,y,z;}s[MAXN*MAXN];
vector<int>P[MAXN*MAXN];map<int,int>Mp;
bool cmp(Edge A,Edge B){return A.z<B.z;}
int Find(int x){return Fa[x]==x?x:Fa[x]=Find(Fa[x]);}
int main(){
	scanf("%d",&N);
	for(int i=1;i<=N;i++)
		for(int j=1;j<=N;j++)
			scanf("%d",&A[i][j]);
	for(int i=1;i<=N;i++){
		if(A[i][i]){
			printf("NOT MAGIC\n");
			return 0;
		}
		for(int j=i+1;j<=N;j++){
			if(A[i][j]!=A[j][i]){
				printf("NOT MAGIC\n");
				return 0;
			}Len++;
			s[Len].x=i;
			s[Len].y=j;
			s[Len].z=A[i][j];
			B[++Cnt]=A[i][j];
		}
	}
	sort(B+1,B+Cnt+1);
	sort(s+1,s+Len+1,cmp);B[0]=-1;
	for(int i=1;i<=Cnt;i++)
		if(B[i]!=B[i-1])Mp[B[i]]=++NCnt;
	for(int i=1;i<=Len;i++){
		s[i].z=Mp[s[i].z];
		P[s[i].z].push_back(i);
	}
	for(int i=1;i<=N;i++)Fa[i]=i;
	for(int i=1;i<=NCnt;i++){
		int size=P[i].size();
		for(int j=0;j<size;j++){
			int u=P[i][j];
			int x=Find(s[u].x);
			int y=Find(s[u].y);
			if(x==y){
				printf("NOT MAGIC\n");
				return 0;
			}
		}
		for(int j=0;j<size;j++){
			int x=Find(s[P[i][j]].x);
			int y=Find(s[P[i][j]].y);
			if(x!=y)Fa[x]=y;
		}
	}
	printf("MAGIC\n");
}