Codeforces Round #313 (Div. 2)

大半年没有打Codeforces ， 昨天开始恢复打Codeforces， 简直是， 欲语泪先流啊。

手残到爆的写错了范围， 手残的数漏了条件， 简直不能直视， 最坑爹的是， E题没时间写代码了。

题目链接

Problem_A:　　

题意：

　　给n个数， 每个数可以用无限次， 求用这些数的和表示不出来的最小的正整数， 没有则输出 -1.

思路：

　　如果这n个数里面有1， 那么一定可以表示所有数， 没有1的话， 最小的正整数就是1

代码：

　　

 1 #include <cmath>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <ctime>
 6 #include <set>
 7 #include <map>
 8 #include <list>
 9 #include <queue>
10 #include <string>
11 #include <vector>
12 #include <fstream>
13 #include <iterator>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 #define LL long long
18 #define MAXN 1000010
19 #define MOD 1000000007
20 #define eps 1e-6
21 int n;
22
23 int main()
24 {
25     bool flag = false;
26     scanf("%d",&n);
27     for(int i = 0; i < n; i ++)
28     {
29         int x;
30         scanf("%d", &x);
31         if(x == 1) flag = true;
32     }
33     printf("%d\n",flag? -1 : 1);
34     return 0;
35 }
36     

Problem_B:

题意：

　　给三个矩形a, b, c。 问是否能将b和c放入a中。

思路：

　　无非四种状态。

　　1）都横着放。

　　2）都竖着放。

　　3）一横一竖。

　　　　①¬， 竖的放在横着的下面。

　　　　②|-，竖的放在横着的旁边。

　　4）连接在一起。

　　　　①--， 横着连在一起。

　　　　②| ， 竖着连在一起。

代码如下：

　　

 1 #include <cmath>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <ctime>
 6 #include <set>
 7 #include <map>
 8 #include <list>
 9 #include <queue>
10 #include <string>
11 #include <vector>
12 #include <fstream>
13 #include <iterator>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 #define LL long long
18 #define MAXN 4
19 #define MOD 1000000007
20 #define eps 1e-6
21 int a[MAXN], b[MAXN];
22 void show()
23 {
24     printf("fuck\n");
25 }
26 bool is_ok()
27 {
28     //1) =
29     if(max(a[1], a[2]) <= a[0] && (b[1] + b[2]) <= b[0]) return true;
30     //2)-- && |
31     if((a[1] + a[2] <= a[0]) && max(b[1], b[2]) <= b[0]) return true;
32     if((a[1] + a[2] <= b[0]) && max(b[1], b[2]) <= a[0]) return true;
33     //3)||
34     if((b[1] + b[2] ) <= a[0] && (max(a[1], a[2]) <= b[0])) return true;
35     //4)|-
36     if((b[1] + a[2] <= a[0]) && ((a[1] >= b[2]? a[1] : b[2]) <= b[0])) return true;
37     if((b[2] + a[1] <= a[0]) && ((a[2] >= b[1]? a[2] : b[1]) <= b[0])) return true;
38     //5)-|
39     if(((a[1] >= b[2]? a[1] : b[2]) <= a[0]) && (b[1] + a[2] <= b[0])) return true;
40     if(((a[2] >= b[1]? a[2] : b[1]) <= a[0]) && (b[2] + a[1] <= b[0])) return true;
41     return false;
42 }
43
44 int main()
45 {
46     for(int i = 0; i < 3; i ++)
47         scanf("%d %d",&a[i], &b[i]);
48     printf(is_ok()?"YES\n":"NO\n");
49     return 0;
50 }

Problem_C:

题意：

　　给一个内角均为120°的六边形（不一定是正六边形）， 问， 能将其分割成多少个单位三角形。

思路：

　　　　

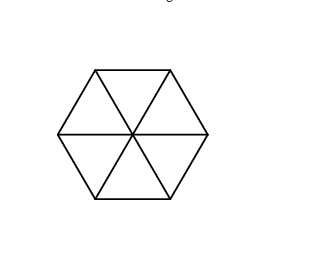
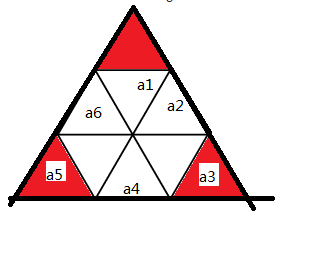
　　将这个六边形的平行边延长， 相交于三点， 构成一个三角形， 可以证明这个三角形为等边三角形。

　　因为六边形内角均为120°， 得到三个红色三角形的两个内角为60°， 所以得大三角形的三个顶角均为60°。

　　所以， 等边三角形的边长为：(a1 + a2 + a3) = (a1 + a6 + a5) = (a1 + a2 + a6) = (a3 + a4 + a5) =....

　　三角形每行有f(x)个单位三角形， x为每行底边长.

　　f(x) = x + x - 1 = 2 * x - 1;

　　f(1) = 1;

　　f(x + 1) - f(x) = 2(x + 1) - 1 - (2 * x  - 1)

　　　　　　　　   = 2

　　得， 解为：s(len) = f(1) + f(2) + ... + f(len), len 为等边三角形边长。

　　　　　　　　　　 =(1 + 2 * x - 1) * x / 2

　　　　　　　　　　 =x ^ 2

　　所以， 边长为n 的等边三角形所含单位三角形数为 s(n)。

　　题目所有的六边形所含单位三角形数为：s(n) - f(a1) - f(a3) - f(a5)。

　　即， 减去三个角的等边三角形， 剩下的就是六边形所包含的

代码如下：

　　

 1 #include <cmath>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <ctime>
 6 #include <set>
 7 #include <map>
 8 #include <list>
 9 #include <queue>
10 #include <string>
11 #include <vector>
12 #include <fstream>
13 #include <iterator>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 #define LL long long
18 #define MAXN 7
19 #define MAXM 4000
20 #define MOD 1000000007
21 #define eps 1e-6
22 int a[MAXN];
23 int fac[MAXM];
24 void init()
25 {
26     fac[0] = 1;
27     for(int i = 1; i < MAXM; i++)
28         fac[i] = i * i;
29 }
30
31 int main()
32 {
33     init();
34     for(int i = 1; i <= 6; i ++)
35         scanf("%d",&a[i]);
36     int ans = fac[a[1] + a[2] + a[3]] - fac[a[1]] - fac[a[3]] - fac[a[5]];
37     printf("%d\n",ans);
38     return 0;
39 }

Problem_D:

题意：

　　给两个字符串a,b， 判断它们是否等价。

　　等价的定义：

　　满足下列条件之一的就是等价。

　　1）a == b

　　2）将字符串a， 分成两部分长度相等的子串a1, a2， b 分成两部分长度相等的子串b1, b2， 满足下列条件之一

　　　　①a1 == b1 并且 a2 == b2

　　　　②a1 == b2 并且 a2 == b1

思路：

　　暴力模拟查找， 也可以hash之后再找， 降低查找的复杂度为O(1)。

　　队友写了一发hash， 我直接暴力的。

　　暴力模拟注意string , cin 会超时， 需要用char[] , scanf()。

代码如下：

　　

 1 #include <cmath>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <ctime>
 6 #include <set>
 7 #include <map>
 8 #include <list>
 9 #include <queue>
10 #include <string>
11 #include <vector>
12 #include <fstream>
13 #include <iterator>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 #define LL long long
18 #define MAXN 2000010
19 #define MOD 1000000007
20 #define eps 1e-6
21 char str_a[MAXN], str_b[MAXN];
22 bool dfs(int pos_a, int pos_b, int len)
23 {
24     if(!strncmp(str_a + pos_a, str_b + pos_b, len)) return true;
25     if(len & 1) return false;
26     int sub_len = len / 2;
27     return (dfs(pos_a , pos_b, sub_len) && dfs(pos_a + sub_len, pos_b + sub_len, sub_len))
28         || (dfs(pos_a + sub_len, pos_b , sub_len) && dfs(pos_a , pos_b + sub_len, sub_len));
29 }
30
31 int main()
32 {
33     scanf("%s %s", str_a, str_b);
34     printf(dfs(0, 0, strlen(str_a)) ? "YES\n" : "NO\n");
35     return 0;
36 }

Problem_E：

题意：

　　给一个h*w的棋盘， 只能往右走， 往下走， 有n个黑格子， 黑格子不能走，问从左上角走到右下角有多少种方案数。

思路：

　　组合数学书上的一个例题，原题只是背景不同。

　　这里利用减法原理， 求出所有经过黑格子的方案数， 再用总的方案数减去就得到答案。

　　sum = C(h - 1 + w - 1, h - 1)

　　设dp[i] 为从左上角不经过任何黑格子走到第i个黑格子的方案数，

　　dp[i] = C(x[i] - 1 + y[i] - 1, x[i] - 1) - sigma(x[j] <= x[i] && y[j] <= y[i]) dp[j] * C(x[i] - x[j] + y[i] - y[j], x[i] - x[j])

　　红色部分为（1，1）到（x[i]，y[[i]）这个矩形区域内， 经过黑格子到（i，j）的方案数。

　　则经过第i个黑格子到达右下角的方案数为：dp[i] * C(h - x[i] + w - y[i], w - [i])。

　　再用sum 减去所有的dp[i]即可。

代码如下：

　　

 #include <cmath>
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <ctime>
 #include <set>
 #include <map>
 #include <list>
 #include <queue>
 #include <string>
 #include <vector>
 #include <fstream>
 #include <iterator>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 #define LL long long
 #define MAXN 2020
 #define MAXM 500010
 #define MOD 1000000007
 #define eps 1e-6
 int w, h, n;
 LL dp[MAXN];
 LL fac[MAXM], fack[MAXM];
 struct node
 {
     int x;
     int y;
 };
 struct node f[MAXN];
 bool cmp(struct node x, struct node y)
 {
     if(x.x == y.x) return x.y < y.y;
     return x.x < y.x;
 }
 LL qpow(LL x, LL k)
 {
     LL res = ;
     while(k)
     {
         if(k & ) res = res * x % MOD;
         x = x * x % MOD;
         k >>= ;
     }
     return res;
 }
 LL C(LL n, LL m)
 {
     if(m <  || m > n) return ;
     return fac[n] * fack[m] % MOD * fack[n-m] % MOD;
 }
 void init()
 {
     fac[] = fack[] = fac[] = fack[] = ;
     for(int i = ; i < MAXM; i ++)
     {
         fac[i] = fac[i-] * i % MOD;
         fack[i] = qpow(fac[i], MOD - );
     }
 }
 
 int main()
 {
     init();
     scanf("%d %d %d", &h, &w, &n);
     for(int i = ; i < n; i ++)
         scanf("%d %d",&f[i].x, &f[i].y);
     memset(dp, , sizeof(dp));
     sort(f, f + n, cmp);
     //ans = C(h + w - 2, h - 1)
     //dp[i] = C(f[i].x + f[i].y - 2, f[i].x - 1) - dp[j] * C(f[i].x - f[j].x + f[i].y - f[j].y, f[i].x - f[j].x)
     //ans -= dp[i] * C(h - f[i].x + w - f[i].y, h -f[i].x)
     LL ans = C(h + w - , h - );
     for(int i = ; i < n; i ++)
     {
         dp[i] = C(f[i].x + f[i].y - , f[i].x - );
         for(int j = ; j < i; j ++)
             if(f[j].x <= f[i].x && f[j].y <= f[i].y)
             {
                 dp[i] -= (dp[j] * C(f[i].x - f[j].x + f[i].y - f[j].y, f[i].x - f[j].x));
                 dp[i] = (dp[i] + MOD) % MOD;
             }
         ans =  ((ans - (dp[i] * C(h - f[i].x + w - f[i].y, h - f[i].x))) % MOD + MOD) % MOD;
     }
     printf("%I64d\n", ans);
     return ;
 }