题解 CF383C 【Propagating tree】

这道题明明没有省选难度啊，为什么就成紫题了QAQ

另：在CF上A了但是洛谷Remote Judge玄学爆零。

---

思路是DFS序+线段树。

首先这道题直观上可以对于每一次修改用DFS暴力O(n)，然后对于询问O(1)解决。

但是这个方法实在是太耗时间了，因此我们想到了dfs序。

所谓dfs序，就是按照dfs（这里我们用先序遍历）的顺序给这颗树打上一个标签。

然后我们就可以把这颗树“拍平”，用一些支持区间修改单点查询的数据结构log级别解决问题了。

---

当然这样粗略地说一遍肯定会有人看不懂，还是通过一个实例讲解好一点。

举个例子，我们有这样一棵树：

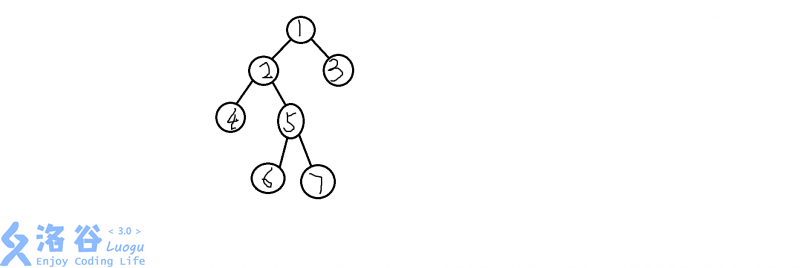
每个节点都有一个编号。现在，我们按照dfs的顺序将这颗树写出来，也就是：

这样这颗树已经被我们“拍平”了，但是仍然无法解题。

为什么？

因为对于每一颗子树，你只知道它从什么地方开始，不知道它在什么地方结束。

解决方案很简单，我们多记录一个out，表示回溯的时候的顺序，这样就可以解决问题了。

dfs这个部分的代码如下：

 void dfs(int x){
     in[x]=++dfn; //in是子树的起点。
     for(int i=head[x];i;i=edge[i].next){
         int y=edge[i].to;
         if(father[x]==y)continue;//father数组储存节点的父亲。（废话）
         dep[y]=dep[x]+,father[y]=x,dfs(y);//dep数组储存节点的深度，这个数组的必要性我们后面会提到。
     }
     out[x]=dfn; //out是子树的中点。
 }

---

然后现在考虑怎么做这道题。

很显然，最大的难点在于每次更新对于每一层节点改变的值都不一样。

等等，每一层？

对的，可以发现，相邻层的节点变化值互为相反数，而相隔层的节点变化值相同。

如果想不出解决方案这道题巨难，但如果想出来了就是一道水题。

很简单，线段树维护节点的变化值，然后在更新时我们对于层数为奇数的节点加上变化值，对于层数为偶数的节点减去变化值。

这样层数为奇数的节点与层数为偶数的节点变化量肯定是反的，也就符合题意。

实现是这样的：

 scanf("%d%d",&op,&x);
 if(op==)scanf("%d",&y),add(,in[x],out[x],dep[x]%?y:-y);
 else printf("%d\n",a[x]+query(,x)*(dep[x]%?:-));

这个玩意的正确性很好说明，自己模拟一下就OK了。

------------

总的来说，这道题就是敲个模板。

代码如下：

 #include<iostream>
 #include<cstdio>
 #define ls p<<1
 #define rs p<<1|1
 using namespace std;
 const int N=;
 int n,m,v,u,cnt,op,x,dfn,y;
 int a[N],in[N],head[N],dep[N],out[N],father[N];
 struct node{int to,next;}edge[N];
 inline void add(int a,int b){edge[++cnt].to=b,edge[cnt].next=head[a],head[a]=cnt;}
 struct tnode{int add,sum,l,r;}tree[N<<];
 void dfs(int x){
     in[x]=++dfn;
     for(int i=head[x];i;i=edge[i].next){
         int y=edge[i].to;
         if(father[x]==y)continue;
         dep[y]=dep[x]+,father[y]=x,dfs(y);
     }
     out[x]=dfn;
 }
 inline void pushup(int p){
     tree[p].sum=tree[ls].sum+tree[rs].sum;
 }
 inline void pushdown(int p,int l,int r){
     if(!tree[p].add)return;
     int mid=(l+r)>>;
     tree[ls].add+=tree[p].add;tree[rs].add+=tree[p].add;
     tree[ls].sum+=tree[p].add*(mid-l+);tree[rs].sum+=tree[p].add*(r-mid);
     tree[p].add=;
 }
 void build(int p,int l,int r){
     tree[p].l=l,tree[p].r=r;
     tree[p].add=tree[p].sum=;
     if(l==r)return;
     int mid=(l+r)>>;
     build(ls,l,mid);build(rs,mid+,r);
     pushup(p);
 }
 void add(int p,int l,int r,int val){
     if(l<=tree[p].l&&tree[p].r<=r){tree[p].add+=val;tree[p].sum+=(tree[p].r-tree[p].l+)*val;return;}
     int mid=(tree[p].l+tree[p].r)>>;
     pushdown(p,tree[p].l,tree[p].r);
     if(l<=mid)add(ls,l,r,val);
     if(r>mid)add(rs,l,r,val);
     pushup(p);
 }
 int query(int p,int x){
     if(tree[p].l==tree[p].r)return tree[p].sum;
     int mid=(tree[p].l+tree[p].r)>>;
     pushdown(p,tree[p].l,tree[p].r);
     if(x<=mid)return query(ls,x);
     else return query(rs,x);
 }
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;++i)scanf("%d",&a[i]);
     for(int i=;i<=n-;++i){
         scanf("%d%d",&v,&u);
         add(v,u);
     }
     dfs();
     build(,,n);
     while(m--){
         scanf("%d%d",&op,&x);
         if(op==)scanf("%d",&y),add(,in[x],out[x],dep[x]%?y:-y);
         else printf("%d\n",a[x]+query(,x)*(dep[x]%?:-));
     }
     return ;
 }