洛谷P3327 [SDOI2015]约数个数和(莫比乌斯反演)

题目描述

设d(x)为x的约数个数，给定N、M，求 \sum^N_{i=1}\sum^M_{j=1}d(ij)∑i=1N​∑j=1M​d(ij)

输入输出格式

输入格式：

输入文件包含多组测试数据。第一行，一个整数T，表示测试数据的组数。接下来的T行，每行两个整数N、M。

输出格式：

T行，每行一个整数，表示你所求的答案。

输入输出样例

输入样例#1： 复制

2
7 4
5 6

输出样例#1： 复制

110
121

说明

1<=N, M<=50000

1<=T<=50000

有一个定理

$d\left(i,j\right) =\sum _{x|i}\sum _{y|j}\left[ \gcd \left( x,y\right) = 1\right]$

然后大力推公式就好了

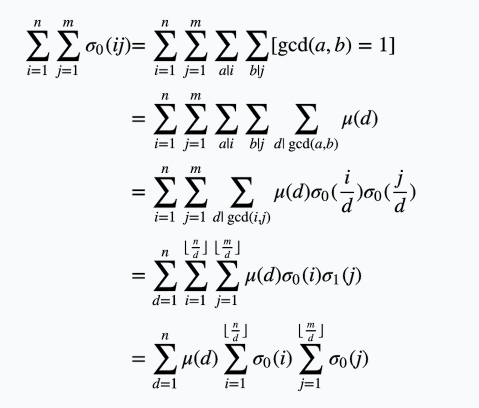
后面两项暴力分块预处理

// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN=1e6+;
inline int read()
{
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int N,M;
int vis[MAXN],prime[MAXN],tot=,mu[MAXN];
long long divv[MAXN];
void GetMu()
{
    vis[]=;mu[]=;
    for(int i=;i<=N;i++)
    {
        if(vis[i]==) prime[++tot]=i,mu[i]=-;
        for(int j=;j<=tot&&i*prime[j]<=N;j++)
        {
            vis[i*prime[j]]=;
            if(i%prime[j]==){mu[i*prime[j]]=;break;}
            else mu[i*prime[j]]=-mu[i];
        }
    }
    for(int i=;i<=N;i++)
        mu[i]+=mu[i-];
    for(int i=;i<=N;i++)
        for(int j=,nxt;j<=i;j=nxt+)
            nxt=i/(i/j),
            divv[i]+=(long long )(nxt-j+)*(i/j);
}
main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
//    freopen("SDOI2015yue.in","r",stdin);
//    freopen("SDOI2015yue.out","w",stdout);
    #endif
    N=;
    GetMu();
    int QWQ=read();
    while(QWQ--)
    {
        long long ans=;
        N=read(),M=read();
        if(N>M) swap(N,M);
        for(int i=,nxt;i<=N;i=nxt+)
        {
            nxt=min(N/(N/i),M/(M/i));
            ans+=(long long )(mu[nxt]-mu[i-])*divv[N/i]*divv[M/i];
        }
        printf("%lld\n",ans);
    }
    return ;
}