左倾堆(三)之 Java的实现

概要

前面分别通过C和C++实现了左倾堆，本章给出左倾堆的Java版本。还是那句老话，三种实现的原理一样，择其一了解即可。

目录
1. 左倾堆的介绍
2. 左倾堆的图文解析
3. 左倾堆的Java实现(完整源码)
4. 左倾堆的Java测试程序

转载请注明出处：http://www.cnblogs.com/skywang12345/p/3638384.html

---

更多内容：数据结构与算法系列 目录

(01) 左倾堆(一)之 图文解析 和 C语言的实现
(02) 左倾堆(二)之 C++的实现
(03) 左倾堆(三)之 Java的实现

左倾堆的介绍

左倾堆(leftist tree 或 leftist heap)，又被成为左偏树、左偏堆，最左堆等。
它和二叉堆一样，都是优先队列实现方式。当优先队列中涉及到"对两个优先队列进行合并"的问题时，二叉堆的效率就无法令人满意了，而本文介绍的左倾堆，则可以很好地解决这类问题。

左倾堆的定义

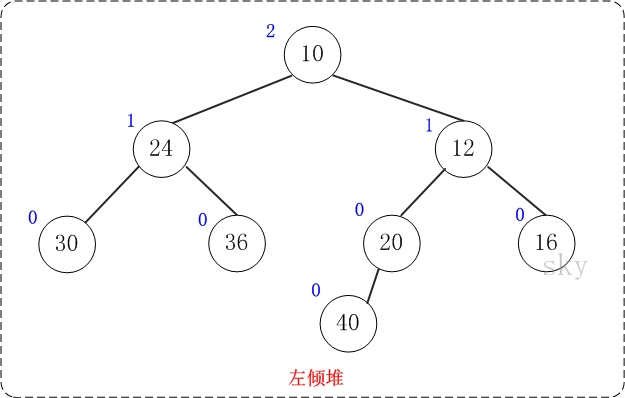
上图是一颗左倾树，它的节点除了和二叉树的节点一样具有左右子树指针外，还有两个属性：键值和零距离。
(01) 键值的作用是来比较节点的大小，从而对节点进行排序。
(02) 零距离(英文名NPL，即Null Path Length)则是从一个节点到一个"最近的不满节点"的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0，NULL节点的NPL为-1。

左倾堆有以下几个基本性质：
[性质1] 节点的键值小于或等于它的左右子节点的键值。
[性质2] 节点的左孩子的NPL >= 右孩子的NPL。
[性质3] 节点的NPL = 它的右孩子的NPL + 1。

左倾堆的图文解析

合并操作是左倾堆的重点。合并两个左倾堆的基本思想如下：
(01) 如果一个空左倾堆与一个非空左倾堆合并，返回非空左倾堆。
(02) 如果两个左倾堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将"较小堆的根节点的右孩子"和"较大堆"进行合并。
(03) 如果新堆的右孩子的NPL > 左孩子的NPL，则交换左右孩子。
(04) 设置新堆的根节点的NPL = 右子堆NPL + 1

下面通过图文演示合并以下两个堆的过程。

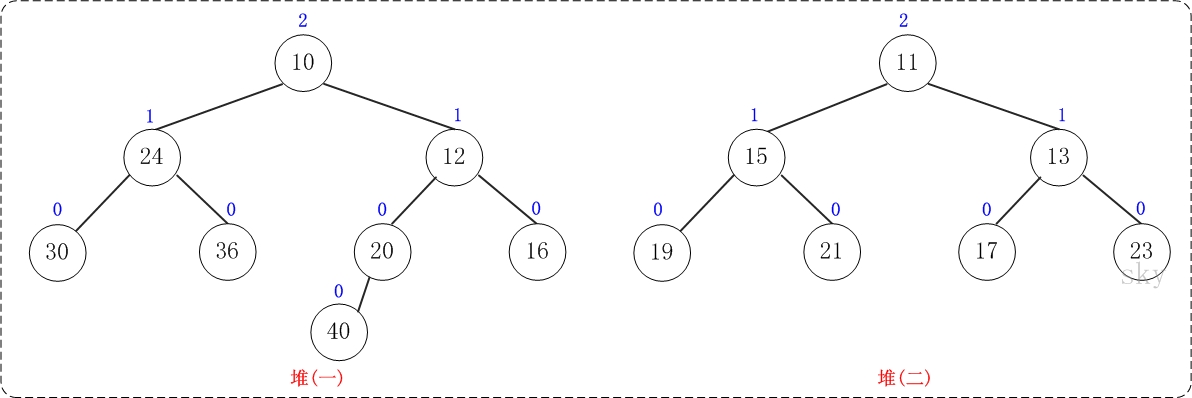
提示：这两个堆的合并过程和测试程序相对应！

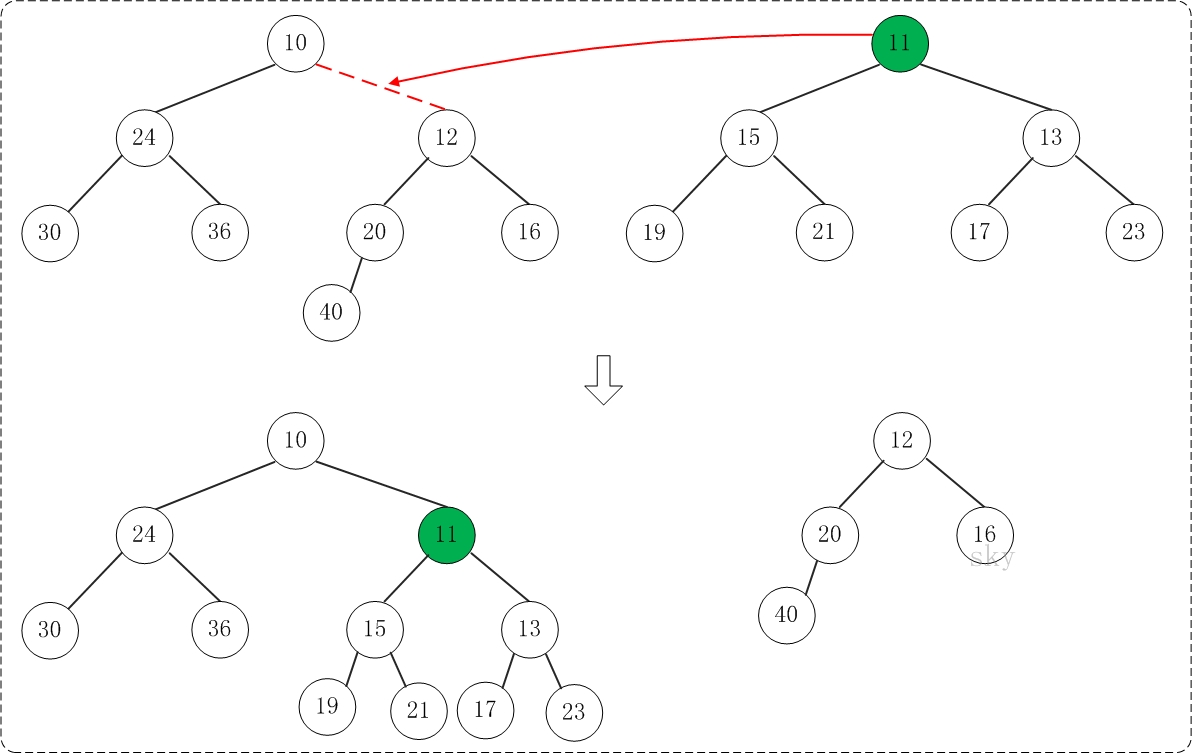
第1步：将"较小堆(根为10)的右孩子"和"较大堆(根为11)"进行合并。
合并的结果，相当于将"较大堆"设置"较小堆"的右孩子，如下图所示：

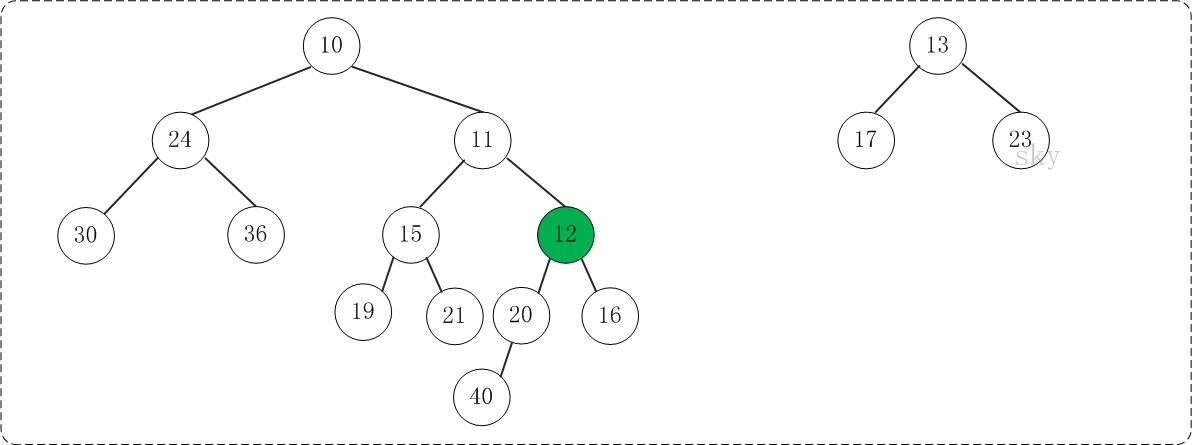
第2步：将上一步得到的"根11的右子树"和"根为12的树"进行合并，得到的结果如下：

第3步：将上一步得到的"根12的右子树"和"根为13的树"进行合并，得到的结果如下：

第4步：将上一步得到的"根13的右子树"和"根为16的树"进行合并，得到的结果如下：

第5步：将上一步得到的"根16的右子树"和"根为23的树"进行合并，得到的结果如下：

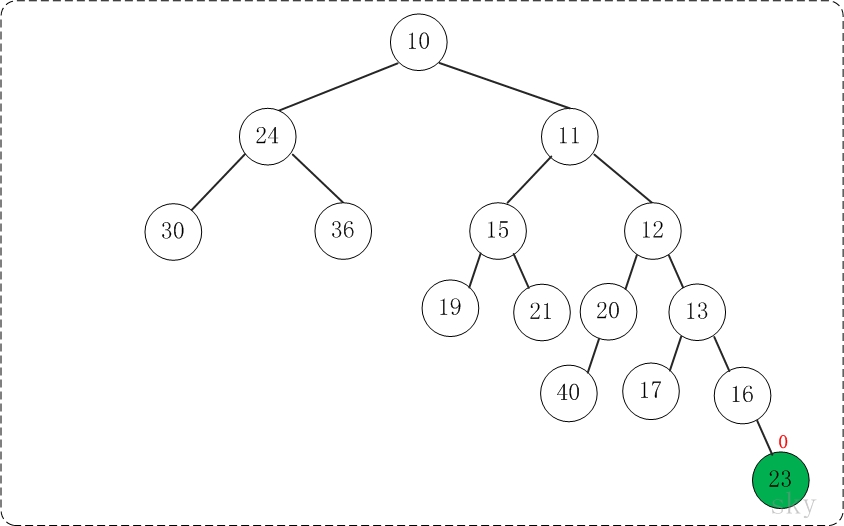
至此，已经成功的将两棵树合并成为一棵树了。接下来，对新生成的树进行调节。

第6步：上一步得到的"树16的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

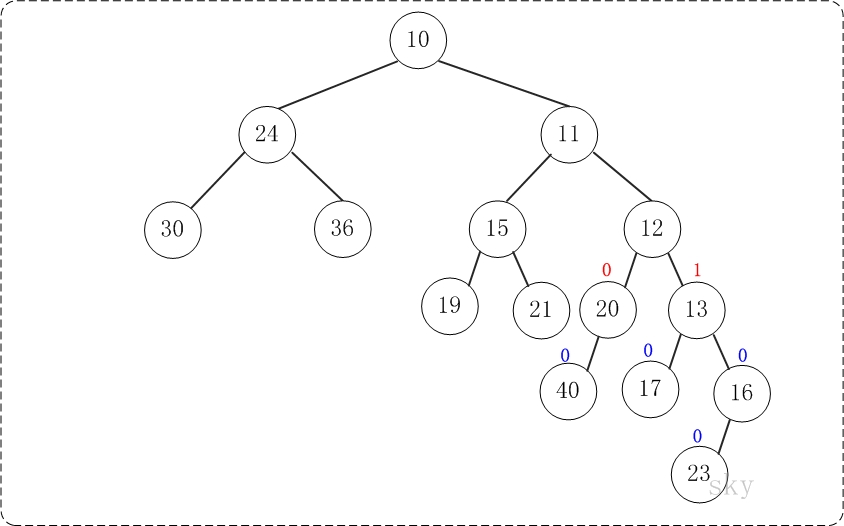
第7步：上一步得到的"树12的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

第8步：上一步得到的"树10的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

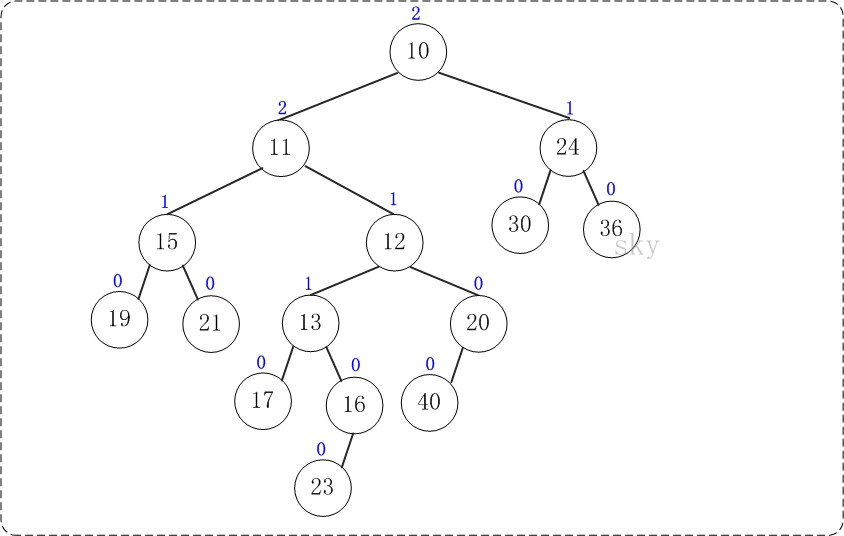
至此，合并完毕。上面就是合并得到的左倾堆！

下面看看左倾堆的基本操作的代码

1. 基本定义

public class LeftistHeap<T extends Comparable<T>> {

    private LeftistNode<T> mRoot;    // 根结点

    private class LeftistNode<T extends Comparable<T>> {
        T key;                    // 关键字(键值)
        int npl;                // 零路经长度(Null Path Length)
        LeftistNode<T> left;    // 左孩子
        LeftistNode<T> right;    // 右孩子

        public LeftistNode(T key, LeftistNode<T> left, LeftistNode<T> right) {
            this.key = key;
            this.npl = 0;
            this.left = left;
            this.right = right;
        }

        public String toString() {
            return "key:"+key;
        }
    }

    ...
}

LeftistNode是左倾堆对应的节点类。
LeftistHeap是左倾堆类，它包含了左倾堆的根节点，以及左倾堆的操作。

2. 合并

/*
 * 合并"左倾堆x"和"左倾堆y"
 */
private LeftistNode<T> merge(LeftistNode<T> x, LeftistNode<T> y) {
    if(x == null) return y;
    if(y == null) return x;

    // 合并x和y时，将x作为合并后的树的根；
    // 这里的操作是保证: x的key < y的key
    if(x.key.compareTo(y.key) > 0) {
        LeftistNode<T> tmp = x;
        x = y;
        y = tmp;
    }

    // 将x的右孩子和y合并，"合并后的树的根"是x的右孩子。
    x.right = merge(x.right, y);

    // 如果"x的左孩子为空" 或者 "x的左孩子的npl<右孩子的npl"
    // 则，交换x和y
    if (x.left == null || x.left.npl < x.right.npl) {
        LeftistNode<T> tmp = x.left;
        x.left = x.right;
        x.right = tmp;
    }
    if (x.right == null || x.left == null)
        x.npl = 0;
    else
        x.npl = (x.left.npl > x.right.npl) ? (x.right.npl + 1) : (x.left.npl + 1);

    return x;
}

public void merge(LeftistHeap<T> other) {
    this.mRoot = merge(this.mRoot, other.mRoot);
}

merge(x, y)是内部接口，作用是合并x和y这两个左倾堆，并返回得到的新堆的根节点。
merge(other)是外部接口，作用是将other合并到当前堆中。

3. 添加

/*
 * 新建结点(key)，并将其插入到左倾堆中
 *
 * 参数说明：
 *     key 插入结点的键值
 */
public void insert(T key) {
    LeftistNode<T> node = new LeftistNode<T>(key,null,null);

    // 如果新建结点失败，则返回。
    if (node != null)
        this.mRoot = merge(this.mRoot, node);
}

insert(key)的作用是新建键值为key的节点，并将其加入到当前左倾堆中。

4. 删除

/*
 * 删除根结点
 *
 * 返回值：
 *     返回被删除的节点的键值
 */
public T remove() {
    if (this.mRoot == null)
        return null;

    T key = this.mRoot.key;
    LeftistNode<T> l = this.mRoot.left;
    LeftistNode<T> r = this.mRoot.right;

    this.mRoot = null;          // 删除根节点
    this.mRoot = merge(l, r);   // 合并左右子树

    return key;
}

remove()的作用是删除左倾堆的最小节点。

注意：关于左倾堆的"前序遍历"、"中序遍历"、"后序遍历"、"打印"、"销毁"等接口就不再单独介绍了。后文的源码中有给出它们的实现代码，Please RTFSC(Read The Fucking Source Code)！

左倾堆的Java实现(完整源码)

左倾堆的实现文件(LeftistHeap.java)

 /**
  * Java 语言: 左倾堆
  *
  * @author skywang
  * @date 2014/03/31
  */

 public class LeftistHeap<T extends Comparable<T>> {

     private LeftistNode<T> mRoot;    // 根结点

     private class LeftistNode<T extends Comparable<T>> {
         T key;                    // 关键字(键值)
         int npl;                // 零路经长度(Null Path Length)
         LeftistNode<T> left;    // 左孩子
         LeftistNode<T> right;    // 右孩子

         public LeftistNode(T key, LeftistNode<T> left, LeftistNode<T> right) {
             this.key = key;
             this.npl = 0;
             this.left = left;
             this.right = right;
         }

         public String toString() {
             return "key:"+key;
         }
     }

     public LeftistHeap() {
         mRoot = null;
     }

     /*
      * 前序遍历"左倾堆"
      */
     private void preOrder(LeftistNode<T> heap) {
         if(heap != null) {
             System.out.print(heap.key+" ");
             preOrder(heap.left);
             preOrder(heap.right);
         }
     }

     public void preOrder() {
         preOrder(mRoot);
     }

     /*
      * 中序遍历"左倾堆"
      */
     private void inOrder(LeftistNode<T> heap) {
         if(heap != null) {
             inOrder(heap.left);
             System.out.print(heap.key+" ");
             inOrder(heap.right);
         }
     }

     public void inOrder() {
         inOrder(mRoot);
     }

     /*
      * 后序遍历"左倾堆"
      */
     private void postOrder(LeftistNode<T> heap) {
         if(heap != null)
         {
             postOrder(heap.left);
             postOrder(heap.right);
             System.out.print(heap.key+" ");
         }
     }

     public void postOrder() {
         postOrder(mRoot);
     }

     /*
      * 合并"左倾堆x"和"左倾堆y"
      */
     private LeftistNode<T> merge(LeftistNode<T> x, LeftistNode<T> y) {
         if(x == null) return y;
         if(y == null) return x;

         // 合并x和y时，将x作为合并后的树的根；
         // 这里的操作是保证: x的key < y的key
         if(x.key.compareTo(y.key) > 0) {
             LeftistNode<T> tmp = x;
             x = y;
             y = tmp;
         }

         // 将x的右孩子和y合并，"合并后的树的根"是x的右孩子。
         x.right = merge(x.right, y);

         // 如果"x的左孩子为空" 或者 "x的左孩子的npl<右孩子的npl"
         // 则，交换x和y
         if (x.left == null || x.left.npl < x.right.npl) {
             LeftistNode<T> tmp = x.left;
             x.left = x.right;
             x.right = tmp;
         }
         if (x.right == null || x.left == null)
             x.npl = 0;
         else
             x.npl = (x.left.npl > x.right.npl) ? (x.right.npl + 1) : (x.left.npl + 1);

         return x;
     }

     public void merge(LeftistHeap<T> other) {
         this.mRoot = merge(this.mRoot, other.mRoot);
     }

     /*
      * 新建结点(key)，并将其插入到左倾堆中
      *
      * 参数说明：
      *     key 插入结点的键值
      */
     public void insert(T key) {
         LeftistNode<T> node = new LeftistNode<T>(key,null,null);

         // 如果新建结点失败，则返回。
         if (node != null)
             this.mRoot = merge(this.mRoot, node);
     }

     /*
      * 删除根结点
      *
      * 返回值：
      *     返回被删除的节点的键值
      */
     public T remove() {
         if (this.mRoot == null)
             return null;

         T key = this.mRoot.key;
         LeftistNode<T> l = this.mRoot.left;
         LeftistNode<T> r = this.mRoot.right;

         this.mRoot = null;          // 删除根节点
         this.mRoot = merge(l, r);   // 合并左右子树

         return key;
     }

     /*
      * 销毁左倾堆
      */
     private void destroy(LeftistNode<T> heap) {
         if (heap==null)
             return ;

         if (heap.left != null)
             destroy(heap.left);
         if (heap.right != null)
             destroy(heap.right);

         heap=null;
     }

     public void clear() {
         destroy(mRoot);
         mRoot = null;
     }

     /*
      * 打印"左倾堆"
      *
      * key        -- 节点的键值
      * direction  --  0，表示该节点是根节点;
      *               -1，表示该节点是它的父结点的左孩子;
      *                1，表示该节点是它的父结点的右孩子。
      */
     private void print(LeftistNode<T> heap, T key, int direction) {

         if(heap != null) {

             if(direction==0)    // heap是根节点
                 System.out.printf("%2d(%d) is root\n", heap.key, heap.npl);
             else                // heap是分支节点
                 System.out.printf("%2d(%d) is %2d's %6s child\n", heap.key, heap.npl, key, direction==1?"right" : "left");

             print(heap.left, heap.key, -1);
             print(heap.right,heap.key,  1);
         }
     }

     public void print() {
         if (mRoot != null)
             print(mRoot, mRoot.key, 0);
     }
 }

左倾堆的测试程序(LeftistHeapTest.java)

 /**
  * Java 语言: 左倾堆
  *
  * @author skywang
  * @date 2014/03/31
  */

 public class LeftistHeapTest {

     public static void main(String[] args) {
         int a[]= {10,40,24,30,36,20,12,16};
         int b[]= {17,13,11,15,19,21,23};
         LeftistHeap<Integer> ha=new LeftistHeap<Integer>();
         LeftistHeap<Integer> hb=new LeftistHeap<Integer>();

         System.out.printf("== 左倾堆(ha)中依次添加: ");
         for(int i=0; i<a.length; i++) {
             System.out.printf("%d ", a[i]);
             ha.insert(a[i]);
         }
         System.out.printf("\n== 左倾堆(ha)的详细信息: \n");
         ha.print();

         System.out.printf("\n== 左倾堆(hb)中依次添加: ");
         for(int i=0; i<b.length; i++) {
             System.out.printf("%d ", b[i]);
             hb.insert(b[i]);
         }
         System.out.printf("\n== 左倾堆(hb)的详细信息: \n");
         hb.print();

         // 将"左倾堆hb"合并到"左倾堆ha"中。
         ha.merge(hb);
         System.out.printf("\n== 合并ha和hb后的详细信息: \n");
         ha.print();
     }
 }

左倾堆的Java测试程序

左倾堆的测试程序已经包含在它的实现文件(LeftistHeapTest.java)中了，这里仅给出它的运行结果：

== 左倾堆(ha)中依次添加: 10 40 24 30 36 20 12 16
== 左倾堆(ha)的详细信息:
10(2) is root
24(1) is 10's   left child
30(0) is 24's   left child
36(0) is 24's  right child
12(1) is 10's  right child
20(0) is 12's   left child
40(0) is 20's   left child
16(0) is 12's  right child

== 左倾堆(hb)中依次添加: 17 13 11 15 19 21 23
== 左倾堆(hb)的详细信息:
11(2) is root
15(1) is 11's   left child
19(0) is 15's   left child
21(0) is 15's  right child
13(1) is 11's  right child
17(0) is 13's   left child
23(0) is 13's  right child

== 合并ha和hb后的详细信息:
10(2) is root
11(2) is 10's   left child
15(1) is 11's   left child
19(0) is 15's   left child
21(0) is 15's  right child
12(1) is 11's  right child
13(1) is 12's   left child
17(0) is 13's   left child
16(0) is 13's  right child
23(0) is 16's   left child
20(0) is 12's  right child
40(0) is 20's   left child
24(1) is 10's  right child
30(0) is 24's   left child
36(0) is 24's  right child