poj 1066 线段相交

链接：http://poj.org/problem?id=1066

Treasure Hunt

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5431		Accepted: 2246

Description

Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors. 
An example is shown below: 

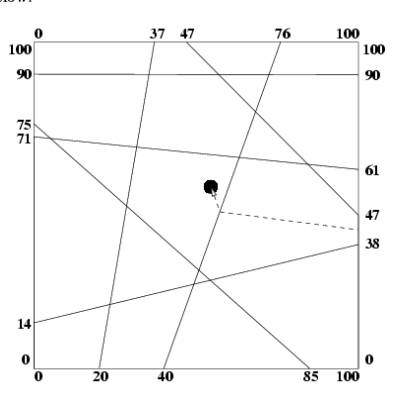
Input

The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall).

Output

Print a single line listing the minimum number of doors which need to be created, in the format shown below.

Sample Input

7
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4 

Sample Output

Number of doors = 2 

Source

East Central North America 1999

 

/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

题意是一个金字塔，从中间某点开始往外走，中间会有许多条线代表许多堵墙，你要算如何能尽快出去，并且炸掉最少的墙

一开始没思路，又看了题是每次从各边中间开始炸，还是没思路，各边中间点没法找啊，n条线，形成n个凸多边形，没法

表示。后来想了一个方法，将边界点（整数点）与目标点连线，求最小相交次数，因为只要可以炸掉走出去，必定可以从一条

直线穿出去。枚举所有边界上的点，求最小交点就是解。同时要注意，线段相交端点相交不能算相交，因为相交点可以直接炸开

算一堵墙。

 

然后就是贴个代码：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <math.h>

#define MAXX 35
#define eps 1e-6
using namespace std;

typedef struct point
{
    double x,y;
} point;
typedef struct line
{
    point st,ed;
} line;

bool dy(double x,double y)
{
    return x>y+eps;
}
bool xy(double x,double y)
{
    return x<y-eps;
}
bool xyd(double x,double y)
{
    return x<y+eps;
}
bool dyd(double x,double y)
{
    return x>y-eps;
}
bool dd(double x,double y)
{
    return fabs(x-y)<eps;
}

double crossProduct(point a,point b,point c)
{
    return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
}

bool onSegment(point a,point b,point  c)
{
    double maxx=max(a.x,b.x);
    double maxy=max(a.y,b.y);
    double minx=min(a.x,b.x);
    double miny=min(a.y,b.y);
    if(dd(crossProduct(a,b,c),0.0)&&xyd(c.x,maxx)&&dyd(c.x,minx)
            &&xyd(c.y,maxy)&&dyd(c.y,miny))
        return true;
    return false;
}

bool segIntersect(point p1,point p2,point p3,point p4)
{
    double d1=crossProduct(p3,p4,p1);
    double d2=crossProduct(p3,p4,p2);
    double d3=crossProduct(p1,p2,p3);
    double d4=crossProduct(p1,p2,p4);
    if(xy(d1*d2,0.0)&&xy(d3*d4,0.0))
        return true;
    /*if(dd(d1,0.0)&&onSegment(p3,p4,p1))
        return true;
    if(dd(d2,0.0)&&onSegment(p3,p4,p2))
        return true;
    if(dd(d3,0.0)&&onSegment(p1,p2,p3))
        return true;
    if(dd(d4,0.0)&&onSegment(p1,p2,p4))
        return  true;
        */
    return false;
}

point p[10010];
line li[MAXX];
int num[MAXX];

int main()
{
    int n,m,i,j;
    point tar;
    while(scanf("%d",&n)!=EOF)
    {
        for(i=0; i<n; i++)
        {
            scanf("%lf%lf%lf%lf",&li[i].st.x,&li[i].st.y,&li[i].ed.x,&li[i].ed.y);
        }
        scanf("%lf%lf",&tar.x,&tar.y);
        i=0;
        int cas=0;
        for(j=1; j<100; j++)
        {
            p[cas].x=0;
            p[cas++].y=j;
        }
        for(j=1; j<100; j++)
        {
            p[cas].x=100;
            p[cas++].y=j;
        }
        for(i=1; i<100; i++)
        {
            p[cas].x=i;
            p[cas++].y=0;
        }
        for(i=1; i<100; i++)
        {
            p[cas].x=i;
            p[cas++].y=100;
        }
        int sum;
        int minn=0x7fffffff;//printf("%d**\n",cas);
        for(i=0; i<cas; i++)
        {
            sum=0;
            for(j=0; j<n; j++)
            {
                if(segIntersect(tar,p[i],li[j].st,li[j].ed))
                {
                    sum++;
                }
            }
            if(minn>sum)
            {
                minn=sum;
            }//printf("%d**\n",sum);
        }
        if(n == 0) printf("Number of doors = 1\n");
        else
            printf("Number of doors = %d\n",minn+1);
    }

    return 0;
}