嵌入式设计模式：有限状态自动机的C语言实现

转自：http://www.cnblogs.com/autosar/archive/2012/06/22/2558604.html

状态机模式是一种行为模式，在《设计模式》这本书中对其有详细的描述，通过多态实现不同状态的调转行为的确是一种很好的方法，只可惜在嵌入式环境下，有时只能写纯C代码，并且还需要考虑代码的重入和多任务请求跳转等情形，因此实现起来着实需要一番考虑。

近日在看了一个开源系统时，看到了一个状态机的实现，也学着写了一个，与大家分享。

首先，分析一下一个普通的状态机究竟要实现哪些内容。

状态机存储从开始时刻到现在的变化，并根据当前输入，决定下一个状态。这意味着，状态机要存储状态、获得输入（我们把它叫做跳转条件）、做出响应。

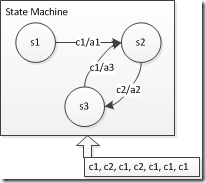
如上图所示，{s1, s2, s3}均为状态，箭头c1/a1表示在s1状态、输入为c1时，跳转到s2，并进行a1操作。

最下方为一组输入，状态机应做出如下反应：

当前状态	输入	下一个状态	动作
s1	c1	s2	a1
s2	c2	s3	a2
s3	c1	s2	a3
s2	c2	s3	a2
s3	c1	s2	a3
s2	c1	s_trap	a_trap
s_trap	c1	s_trap	a_trap

当某个状态遇到不能识别的输入时，就默认进入陷阱状态，在陷阱状态中，不论遇到怎样的输入都不能跳出。

为了表达上面这个自动机，我们定义它们的状态和输入类型：

 typedef int State;
 typedef int Condition;

 #define STATES 3 + 1
 #define STATE_1 0
 #define STATE_2 1
 #define STATE_3 2
 #define STATE_TRAP 3

 #define CONDITIONS 2
 #define CONDITION_1 0
 #define CONDITION_2 1

在嵌入式环境中，由于存储空间比较小，因此把它们全部定义成宏。此外，为了降低执行时间的不确定性，我们使用O(1)的跳转表来模拟状态的跳转。

首先定义跳转类型：

 typedef void (*ActionType)(State state, Condition condition);

 typedef struct
 {
     State next;
     ActionType action;
 } Trasition, * pTrasition;

然后按照上图中的跳转关系，把三个跳转加一个陷阱跳转先定义出来：

 // (s1, c1, s2, a1)
 Trasition t1 = {
     STATE_2,
     action_1
 };

 // (s2, c2, s3, a2)
 Trasition t2 = {
     STATE_3,
     action_2
 };

 // (s3, c1, s2, a3)
 Trasition t3 = {
     STATE_2,
     action_3
 };

 // (s, c, trap, a1)
 Trasition tt = {
     STATE_TRAP,
     action_trap
 };

其中的动作，由用户自己完成，在这里仅定义一条输出语句。

 void action_1(State state, Condition condition)
 {
     printf("Action 1 triggered.\n");
 }

最后定义跳转表：

 pTrasition transition_table[STATES][CONDITIONS] = {
 /*      c1,  c2*/
 /* s1 */&t1, &tt,
 /* s2 */&tt, &t2,
 /* s3 */&t3, &tt,
 /* st */&tt, &tt,
 };

即可表达上文中的跳转关系。

最后定义状态机，如果不考虑多任务请求，那么状态机仅需要存储当前状态便行了。例如：

 typedef struct
 {
     State current;
 } StateMachine, * pStateMachine;

 State step(pStateMachine machine, Condition condition)
 {
     pTrasition t = transition_table[machine->current][condition];
     (*(t->action))(machine->current, condition);
     machine->current = t->next;
     return machine->current;
 }

但是考虑到当一个跳转正在进行的时候，同时又有其他任务请求跳转，则会出现数据不一致的问题。

举个例子：task1(s1, c1/a1 –> s2)和task2(s2, c2/a2 –> s3)先后执行，是可以顺利到达s3状态的，但若操作a1运行的时候，执行权限被task2抢占，则task2此时看到的当前状态还是s1，s1遇到c2就进入陷阱状态，而不会到达s3了，也就是说，状态的跳转发生了不确定，这是不能容忍的。

因此要重新设计状态机，增加一个“事务中”条件和一个用于存储输入的条件队列。修改后的代码如下:

 #define E_OK        0
 #define E_NO_DATA   1
 #define E_OVERFLOW  2

 typedef struct
 {
     Condition queue[QMAX];
     int head;
     int tail;
     bool overflow;
 } ConditionQueue, * pConditionQueue;

 int push(ConditionQueue * queue, Condition c)
 {
     unsigned int flags;
     Irq_Save(flags);
     if ((queue->head == queue->tail + ) || ((queue->head == ) && (queue->tail == )))
     {
         queue->overflow = true;
         Irq_Restore(flags);
         return E_OVERFLOW;
     }
     else
     {
         queue->queue[queue->tail] = c;
         queue->tail = (queue->tail + ) % QMAX;
         Irq_Restore(flags);
     }
     return E_OK;
 }

 int poll(ConditionQueue * queue, Condition * c)
 {
     unsigned int flags;
     Irq_Save(flags);
     if (queue->head == queue->tail)
     {
         Irq_Restore(flags);
         return E_NO_DATA;
     }
     else
     {
         *c = queue->queue[queue->head];
         queue->overflow = false;
         queue->head = (queue->head + ) % QMAX;
         Irq_Restore(flags);
     }
     return E_OK;
 }

 typedef struct
 {
     State current;
     bool inTransaction;
     ConditionQueue queue;
 } StateMachine, * pStateMachine;

 static State __step(pStateMachine machine, Condition condition)
 {
     State current = machine -> current;
     pTrasition t = transition_table[current][condition];
     (*(t->action))(current, condition);
     current = t->next;
     machine->current = current;
     return current;
 }

 State step(pStateMachine machine, Condition condition)
 {
     Condition next_condition;
     int status;
     State current;
     if (machine->inTransaction)
     {
         push(&(machine->queue), condition);
         return STATE_INTRANSACTION;
     }
     else
     {
         machine->inTransaction = true;
         current = __step(machine, condition);
         status = poll(&(machine->queue), &next_condition);
         while(status == E_OK)
         {
             __step(machine, next_condition);
             status = poll(&(machine->queue), &next_condition);
         }
         machine->inTransaction = false;
         return current;
     }
 }

 void initialize(pStateMachine machine, State s)
 {
     machine->current = s;
     machine->inTransaction = false;
     machine->queue.head = ;
     machine->queue.tail = ;
     machine->queue.overflow = false;
 }