层次分析模型（AHP）及其MATLAB实现

　　 今天用将近一天的时间学习了层次分析模型（AHP），主要参考了一份pdf，这个网站，和暨南大学章老师的课件，现写出一些自己总结的要点。　　

　　一、层次分析法的基本步骤：

角度一：

实际问题——分解——>多个因素——建立——>层次结构—

—确定——>诸因素的相对重要性——计算——>权向量—

—判断——>综合决策

角度二：

建立层次结构模型——>构造判断矩阵——>层次单排序——>一致性检验——>层次总排序。

　　二、几个理解的重点

1.正反矩阵

若矩阵A=（aij)mxn满足以下特征：

(1) aij>0

(2)aij=1/aji

则称矩阵A 为正互反矩阵。

2.一致阵

定义：满足a(ij)·a(jk)=a(ik), i,j,k=1,2,··,n的正互反阵A称一致阵。

性质：A的秩为1，A的唯一非0特征根为n;

　　　A的任一列向量是对应于n的特征向量；

　　　A的归一化特征向量可作为权向量。

注意：

这里想了下，用最大特征根的特征向量替代A，可能是为了最大限度的保存原始数据（A）的信息量（不确定。。。）

3.一致性检验

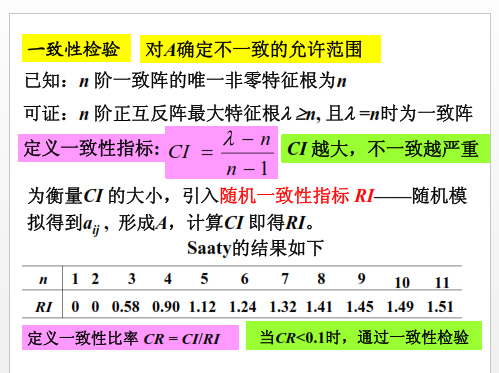
一致性检验，具体还要涉及组合一致性检验。

 　　三、MATLAB实现

这里先是搜的资料，看到这段代码，代码写得很清晰，这里直接贴在这里。

clc;
clear;
A=[1 1.2 1.5 1.5;
0.833  1 1.2 1.2;
0.667  0.833  1 1.2;
0.667  0.833  0.833  1];
                                   %因素对比矩阵A，只需要改变矩阵A
[m,n]=size(A);                     %获取指标个数
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];
R=rank(A);                         %求判断矩阵的秩
[V,D]=eig(A);                      %求判断矩阵的特征值和特征向量，V特征值，D特征向量；
tz=max(D);
B=max(tz);                         %最大特征值
[row, col]=find(D==B);             %最大特征值所在位置
C=V(:,col);                        %对应特征向量
CI=(B-n)/(n-1);                    %计算一致性检验指标CI
CR=CI/RI(1,n);
if CR<0.10
    disp('CI=');disp(CI);
    disp('CR=');disp(CR);
    disp('对比矩阵A通过一致性检验，各向量权重向量Q为：');
    Q=zeros(n,1);
    for i=1:n
        Q(i,1)=C(i,1)/sum(C(:,1)); %特征向量标准化
    end
    Q                              %输出权重向量
else
    disp('对比矩阵A未通过一致性检验，需对对比矩阵A重新构造');
end

　　这里是对AHP的一个初步的认识，之后还要深入学习，到时候再继续总结。

　　#############2016-10-11补更#######################

　　今天交流群有人问起AHP的一个问题，不太会，就回来再次复习一下，又学到一点知识。看看之前写的，感觉好乱。。。也不删除了，就当个预备知识和。。娱乐吧。

　　这里主要写下一些要点和细节。

　　一、AHP流程

　　1.建立层次结构模型

　　2.构建Z-C判断矩阵，设为A。

　　这里我们要确定准则层C中，各个因素的权重，为此我们要计算判断矩阵A的最大的特征值及其特征向量。

此时，我们要对A进行一致性检验，只有A为一致阵（关于一致阵，前文有说明）或者其不一致程度在一个特定范围内时，才能将其特征根对应的特征向量作为被比较因素的权量。

一般情况下，矩阵A是不一致的，所以我们此时要进行一致性检验（具体在前文也有说明）。

　　通过一致性检验后，就计算得到A的最大特征值及其对应的特征向量，这个特征向量即为各个准则的权重。

　　3.构建C-P矩阵，层次单排序。

　　对应的特征向量矩阵如下：

　　

　　这个矩阵的每一行代表一个候选人的在健康，知识业务等六个方面的权重大小。

　 4.构建Z-P矩阵，层次总排序，决策。

　　总的来说AHP还是那句，先分解再综合。拿上面的例子来说，我要从三人中选一名领导，那么我通过6个不同的角度来为这三人打分，首先确定这6个角度在你心目中的比重大小（Z-C），之后再通过对比看三人分别在这6个角度的得分(C-P)。最后再和对应角度的权重相乘(Z-P)，就得到总的分数，排序，作出决策。