【机器学习】支持向量机（SVM）

感谢中国人民大学胡鹤老师，课程深入浅出，非常好

一、关于SVM

可以做线性分类、非线性分类、线性回归等，相比逻辑回归、线性回归、决策树等模型（非神经网络）功效最好

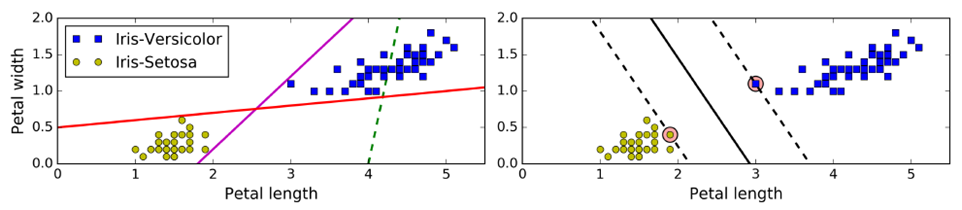
传统线性分类：选出两堆数据的质心，并做中垂线（准确性低）——上图左

SVM：拟合的不是一条线，而是两条平行线，且这两条平行线宽度尽量大，主要关注距离车道近的边缘数据点（支撑向量support vector），即large margin classification——上图右

使用前，需要对数据集做一个scaling，以做出更好的决策边界（decision boundary）

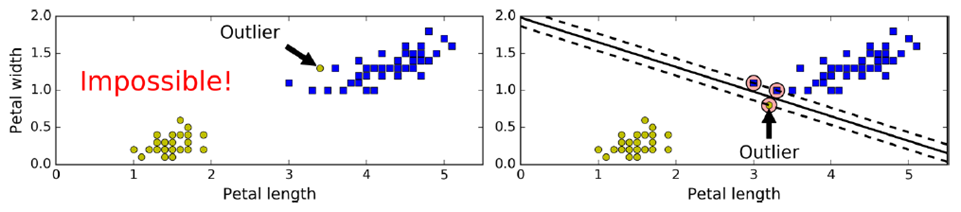
但需要容忍一些点跨越分割界限，提高泛化性，即softmax classification

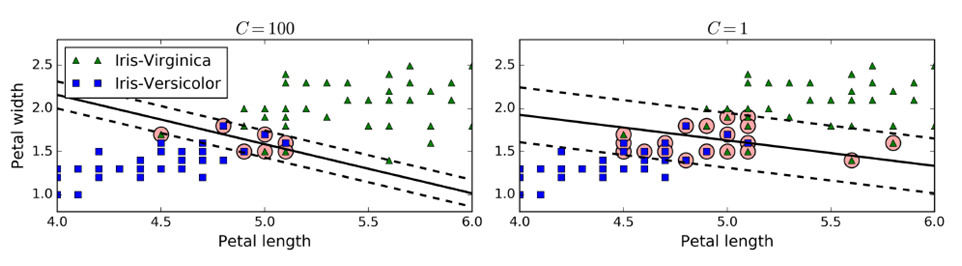
在sklearn中，有一个超参数c，控制模型复杂度，c越大，容忍度越小，c越小，容忍度越高。c添加一个新的正则量，可以控制SVM泛化能力，防止过拟合。（一般使用gradsearch）

SVM特有损失函数Hinge Loss

二、LinearSVC(liblinear库，不支持kernel函数，但是相对简单，复杂度O(m*n)）

同SVM特点吻合，仅考虑落在分类面附近和越过分类面到对方领域的向量，给于一个线性惩罚（l1），或者平方项（l2）

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris["data"][:,(2,3)]
y = (iris["target"]==2).astype(np.float64)
svm_clf = Pipeline((
    ("scaler",StandardScaler()),
    ("Linear_svc",LinearSVC(C=1,loss="hinge")),
    ))
svm_clf.fit(X,y)
print(svm_clf.predit([[5.5,1.7]]))

三、对于nonlinear数据的分类

　　有两种方法，构造高维特征，构造相似度特征

1. 使用高维空间特征（即kernel的思想），将数据平方、三次方。。映射到高维空间上

from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline((
     ("poly_features", PolynomialFeatures(degree=3)),
     ("scaler", StandardScaler()),
     ("svm_clf", LinearSVC(C=10, loss="hinge"))
   ))
polynomial_svm_clf.fit(X, y)

这种kernel trick可以极大地简化模型，不需要显示的处理高维特征，可以计算出比较复杂的情况

但模型复杂度越强，过拟合风险越大

SVC（基于libsvm库，支持kernel函数，但是相对复杂，不能用太大规模数据，复杂度O(m^2 *n)-O(m^3 *n)）

可以直接使用SVC（coef0：高次与低次权重）

from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline((
      ("scaler", StandardScaler()),
      ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ))
poly_kernel_svm_clf.fit(X, y)

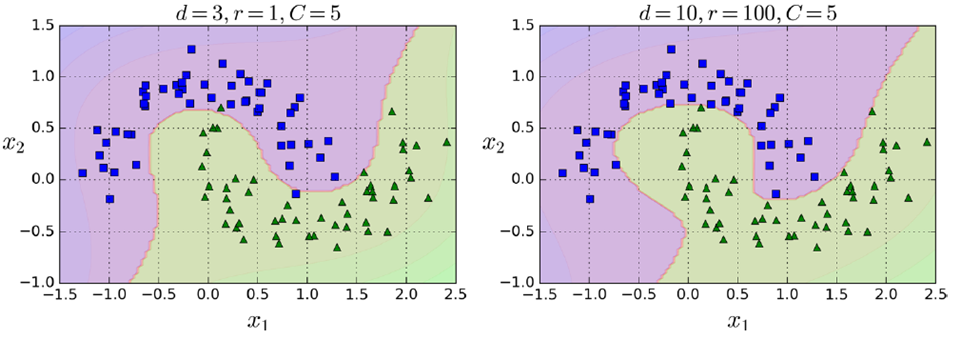
2. 添加相似度特征（similarity features）

例如，下图分别创造x1,x2两点的高斯分布，再创建新的坐标系统，计算高斯距离（Gaussian RBF Kernel径向基函数）

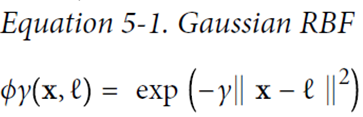
gamma（γ）控制高斯曲线形状胖瘦，数据点之间的距离发挥更强作用

rbf_kernel_svm_clf = Pipeline((
      ("scaler", StandardScaler()),
      ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
   ))
rbf_kernel_svm_clf.fit(X, y)

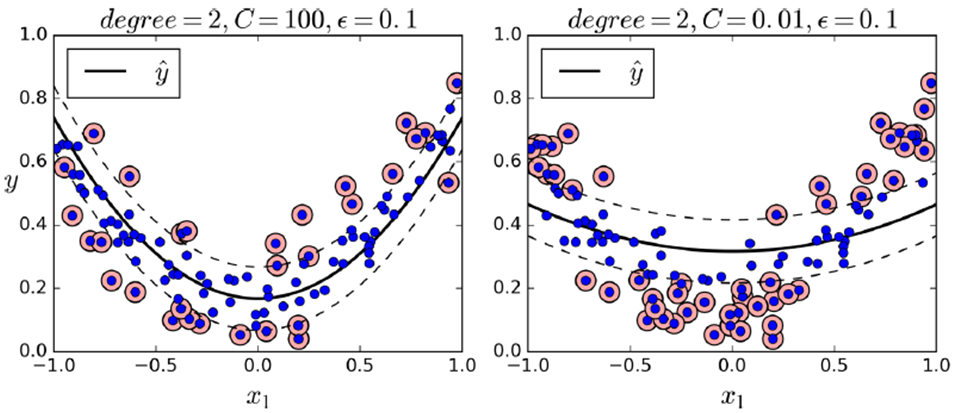
如下是不同gamma和C的取值影响

SGDClassifier(支持海量数据，时间复杂度O(m*n))

四、SVM Regression（SVM回归）

尽量让所用instance都fit到车道上，车道宽度使用超参数控制，越大越宽

使用LinearSVR

from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)

使用SVR

from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)

五、数学原理：

w通过控制h倾斜的角度，控制车道的宽度，越小越宽，并且使得违反分类的数据点更少

1. hard margin linear SVM

优化目标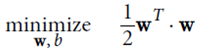：，并且保证

2. soft margin linear SVM

增加一个新的松弛变量（slack variable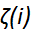），起正则化作用

优化目标：，并且保证

放宽条件，即使有个别实例违反条件，也惩罚不大

3. LinearSVM

使用拉格朗日乘子法进行计算，α是松弛项后的结果

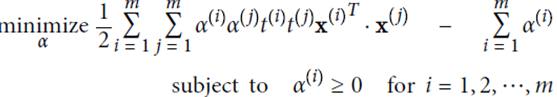
计算结果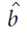：取平均值

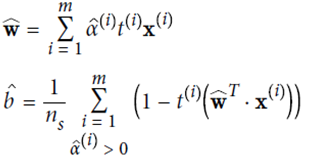
KernelizedSVM

由于

故可先在低位空间里做点积计算，再映射到高维空间中。

下列公式表示，在高维空间计算可用kernel trick方式，直接在低维上面计算

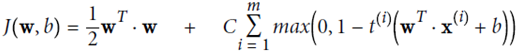
几个常见的kernal及其function