CPP--正码，反码，补码~附整数溢出的探讨

之前说到了long的争议（http://www.cnblogs.com/dotnetcrazy/p/8059210.html），这边就不用long来举例了，用int吧

可以看一下这篇文章（http://www.cnblogs.com/dotnetcrazy/p/6743530.html），更好理解本文（本文不继续探讨大小端对齐问题，只研究标题内容）

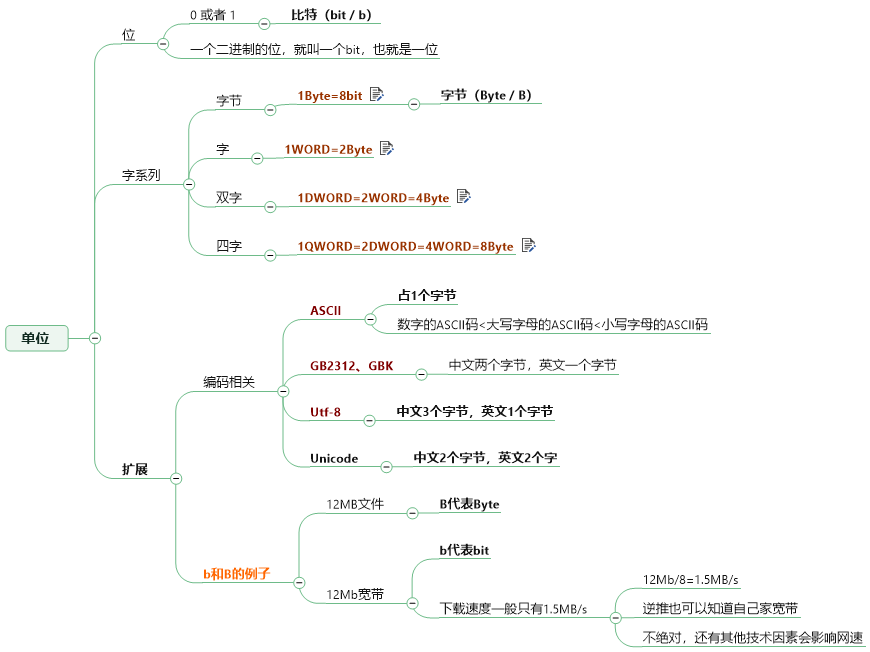
1.基础就不详解了贴张图：

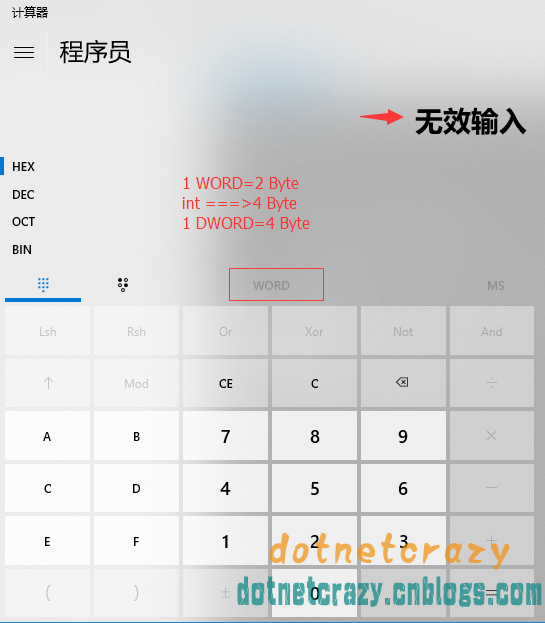
说一下QWORD，之前也被网上误导了，网上很多都是说无符号的word，按照惯例，如果是unsigned word，那么所占字节应该和word一样才对

验证：有无符号，他所占字节并不变

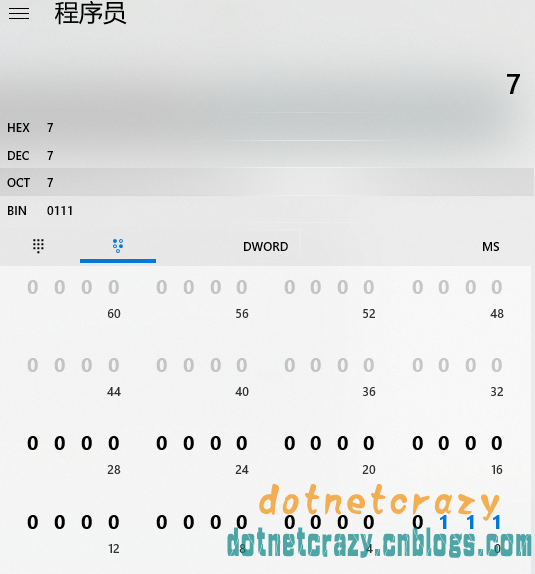
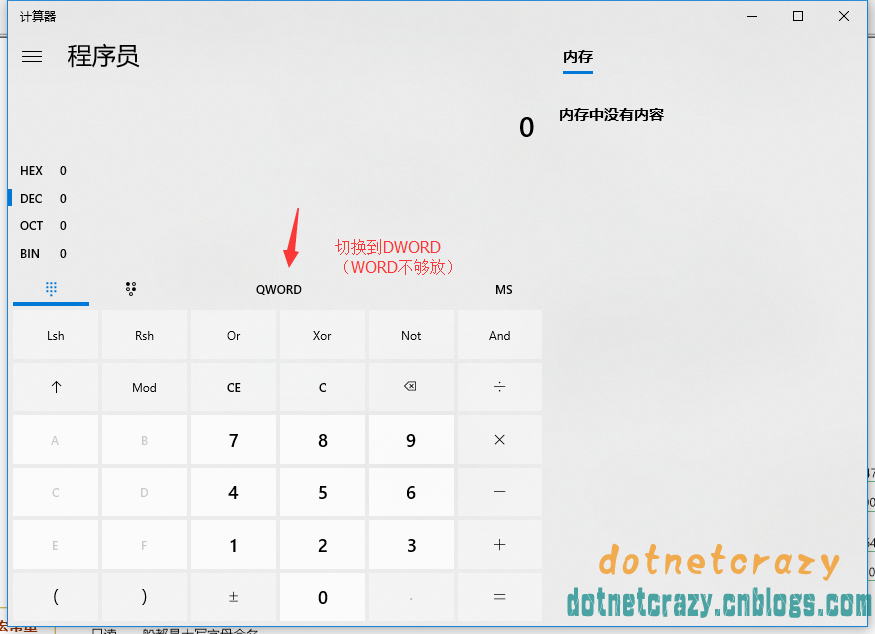
后来发现Win10最新版有一计算器神器（你们可以通过应用商城装）===》

通过7来说说这些“字”宝宝们（我后面说补码计算的时候也会用到这个案例）

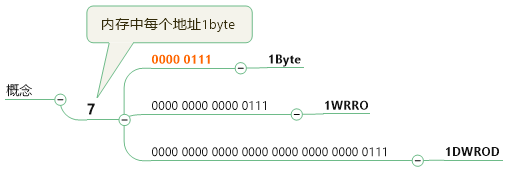
1Byte=8bit（一个二进制位就是一个bit）

7==》0000 0111

1WORD=2Byte，7==》0000 0000 0000 0111

1DWORD=4Byte，7==》0000 0000 0000 0000 0000 0000 0000 0111

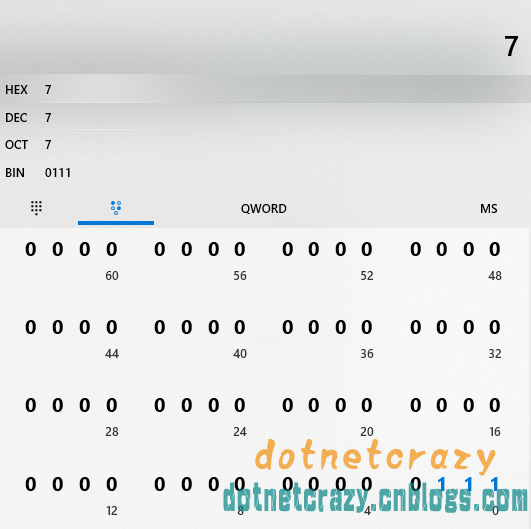
重点来了，要是QWORD真的是WORD无符号字，那么应该和WORD一样只占2Byte

然而事实==》打脸打的PaPa响，1QWORD=8Byte，7==》以下省略一千字

2.原码，反码，补码

在计算机内，有符号数有3种表示法：原码、反码和补码

原码：计算机中对数字的二进制定点表示方法。最高位为符号位（正数该位为0，负数该位为1）其余位表示数值的大小

反码：正数的反码与其原码相同，负数的反码：符号位不动，其他取反

补码：正数的补码和原码相同，负数的补码：符号位不动，其他取反，最后+1（相当于：补码+1）

补码的好处：使符号位能与有效值部分一起参加运算,从而简化运算规则；使符号位能与有效值部分一起参加运算,从而简化运算规则

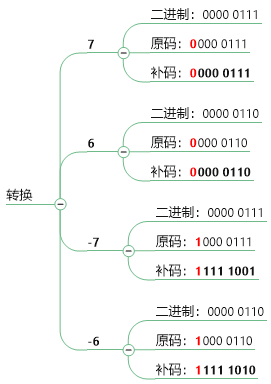
来张图更直观：

来来来，实践验证一下：

分析：按照求负数补码的逆过程，数值部分应是最低位减1，然后取反。
但是对二进制数来说，先减1后取反和先取反后加1得到的结果是一样的，故仍可采用取反加1 的方法。

这些都比较简单，下面说下补码的好处：

体验分析一下

7-6=1；-7+6=-1

7-6=1

7补码：0000 0111

-6补码：1111 1010

  0000 0111
  1111 1010
  ---------
1 0000 0001

进位舍弃（总共就8位，溢出就没了），0000 0001==>1（正数的补码是他本身）

-7+6=-1

-7补码：1111 1001

6补码：0000 0110

1111 1001
0000 0110
---------
1111 1111

木有进位，补码：1111 1111，正码（符号位不动，其他取反，最后+1）：1000 0001==>-1

扩展（有兴趣的可以自己研究一下补码的各种溢出）：https://baike.baidu.com/item/反码#5

3.整数溢出探讨

 intmax=0x7FFFFFFF; （2147483647）

不清楚的可以看这个图，第一位是符号位，后面是数值部分，所以第一个最大是7，其他最大是F

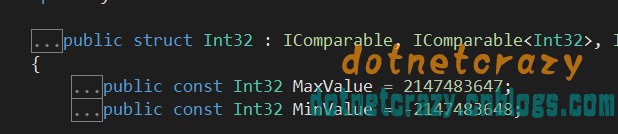
借用Net里面的Int.Max验证下：2147483647

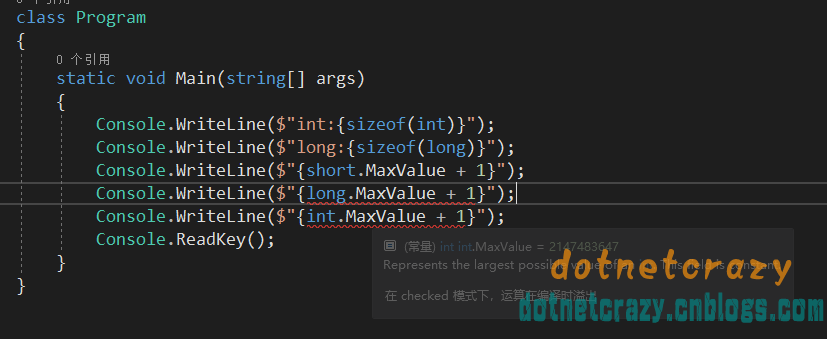
不高兴搞需的，毕竟不是学生了，直接跑个程序看看

int main() {
 int i = 0x7fffffff;
 printf("i=%X==>%d\n", i, i);
 i += 1;
 printf("i+1=%d==>%X\n", i, i);
 return 0;
}

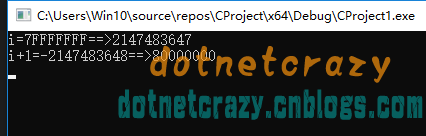
CentOS_X64：i+1=-2147483648==>0x80000000

Win10_X64：i+1=-2147483648==>0x80000000

记得以前学生时代就很不解，老师也说不清楚，这次看见了就研究了下

来来来，Net来个福利：自己研究下为啥

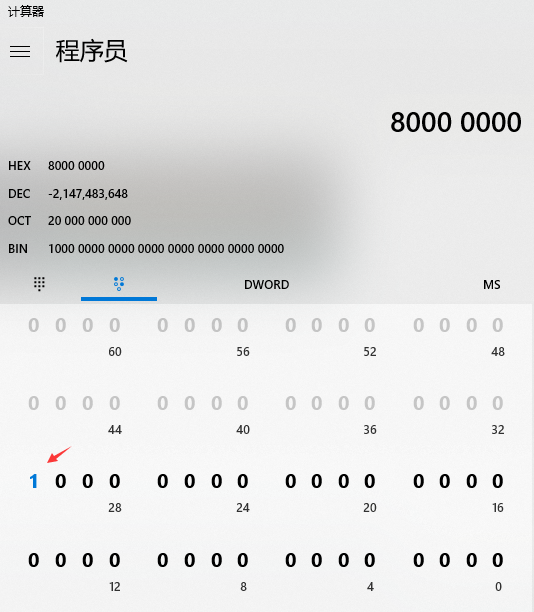
不扯了，二进制走一个：（二进制是不管符号位啥的，输出的八进制和十六进制其实都是unsigned int （%o,%x））

0111 1111 1111 1111  1111 1111 1111 1111
                                       +1
1000 0000 0000 0000  0000 0000 0000 0000
———— ———— ———— ————  ———— ———— ———— ————
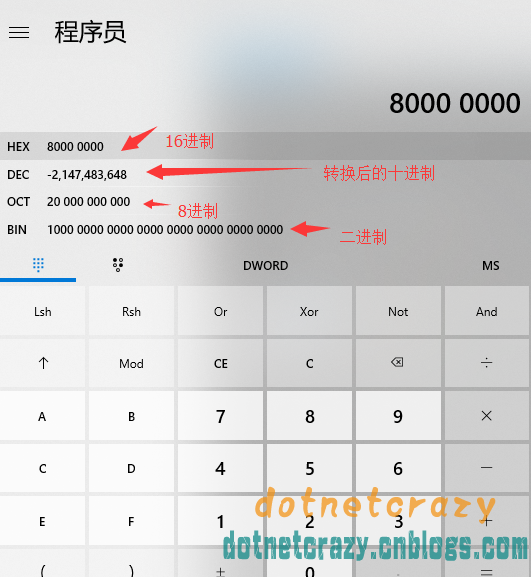
 8    0    0    0     0    0    0     0

intmax+1=0x80000000，程序员还是比较喜欢十六进制啊~方便

可能你还没转过来，(⊙o⊙)…，好吧，我们用补码的方式再算一遍

0111 1111 1111 1111  1111 1111 1111 1111
0000 0000 0000 0000  0000 0000 0000 0001
---- ---- ---- ----  ---- ---- ---- ----
1000 0000 0000 0000  0000 0000 0000 0000

转为正码：
1000 0000 0000 0000 0000 0000 0000 0000 补码
1111 1111 1111 1111 1111 1111 1111 1111 正码

2^31==>2147483648，符号位是1，则最后结果是-2147483648

------------------------------------------

收工了，感兴趣的可以用Win10计算神器看看（用QWORD又是怎样呢，可以自己思考，很有意思哦）

稍微解释一下：word是2Byte，intmax是4Byte，所以不够放

在选下HEX，输入运算得到的数字