Nowcoder OI赛制测试2 F 假的数学题 - 斯特林公式 + 二分

Description

给定$X$， 找到最小的$N$ 使得$N! > X^X$

数据范围：  $x <= 1e11$

Solution

$X^X$ 太大， 高精也存不过， 所以取对数 : $lg(X^X)$ = Xlg(X)，即要求出最小$N$的使得$lg(N!) > Xlg(X)$

N!有单调性， 可以使用二分答案来求出N， 但是每次$check$的复杂度是$O(N)$， 我们必须要进行优化。

通过斯特林公式 : 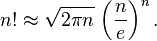      ， 取对数后:  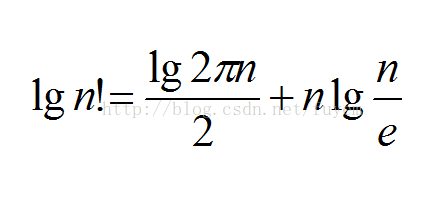  (图片都是转发的QuQ）

就可以在$O(1)$时间内算出$lg(N!)$ 并check。 总复杂度$O(logN)$

Code

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #define lb long double
 #define ll long long
 #define e 2.7182818284590453254
 using namespace std;

 lb n, x;

 bool check(ll o) {
     lb pi = acos(-);
     n = o;
     n = log( * pi * n) /  + n * log(n / e);
     if(n > x) return ;
     else return ;
 }

 int main()
 {
     scanf("%llf", &x);
     x = x * log(x);
     ll l = , r = 1e18, ans = ;
     while(l <= r) {
         ll mid = (l + r) >> ;
         if(check(mid)) ans = mid, r = mid - ;
         else l = mid + ;
     }
     printf("%lld\n", ans);
 }