[AI]神经网络章1 神经网络基本工作原理

神经元细胞的数学计算模型

神经网络由基本的神经元组成，下图就是一个神经元的数学/计算模型，便于我们用程序来实现。

输入

(x1,x2,x3) 是外界输入信号，一般是一个训练数据样本的多个属性，比如，我们要识别手写数字0~9，那么在手写图片样本中，x1可能代表了笔画是直的还是有弯曲，x2可能代表笔画所占面积的宽度，x3可能代表笔画上下两部分的复杂度。

(W1,W2,W3) 是每个输入信号的权重值，以上面的 (x1,x2,x3) 的例子来说，x1的权重可能是0.5，x2的权重可能是0.2，x3的权重可能是0.3。当然权重值相加之后可以不是1。

还有个b是干吗的？一般的书或者博客上会告诉你那是因为y=wx+by=wx+b，b是偏移值，使得直线能够沿Y轴上下移动。这是用结果来解释原因，并非b存在的真实原因。从生物学上解释，在脑神经细胞中，一定是输入信号的电平/电流大于某个临界值时，神经元细胞才会处于兴奋状态，这个b实际就是那个临界值。亦即当：

w1∗x1+w2∗x2+w3∗x3>=t时，该神经元细胞才会兴奋。我们把t挪到等式左侧来，变成(−t)(−t)，然后把它写成b，变成了： w1∗x1+w2∗x2+w3∗x3+b>=0 

于是b诞生了！

求和计算

Z=w1∗x1+w2∗x2+w3∗x3+b=∑(wi∗xi)+b

激活函数

求和之后，神经细胞已经处于兴奋状态了，已经决定要向下一个神经元传递信号了，但是要传递多强烈的信号，要由激活函数来确定：

A=σ(Z)

如果激活函数是一个阶跃信号的话，那受不了啊，你会觉得脑子里总是一跳一跳的，像继电器开合一样咔咔乱响，所以一般激活函数都是有一个渐变的过程，也就是说是个曲线。

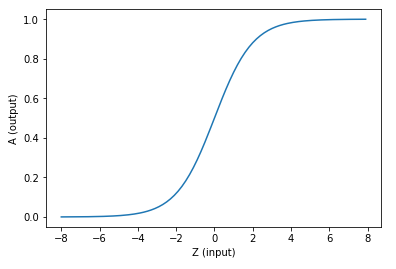
激活函数的更多描述在后续的博客中。

至此，一个神经元的工作过程就在电光火石般的一瞬间结束了。

神经网络的基本训练过程

单层神经网络模型

这是一个单层的神经网络，有m个输入 (这里m=3)，有n个输出 (这里n=2)。在单个神经元里，b是个值。但是在神经网络中，我们把b的值永远设置为1，而用b到每个神经元的权值来表示实际的偏移值，亦即(b1,b2)，这样便于矩阵运算。也有些作者把b写成x0，其实是同一个意思，只不过x0用于等于1。

• (x1,x2,x3)是一个样本数据的三个特征值
• (w11,w12,w13)是(x1,x2,x3)到n1的权重
• (w21,w22,w23)是(x1,x2,x3)到n2的权重
• b1是n1的偏移
• b2是n2的偏移

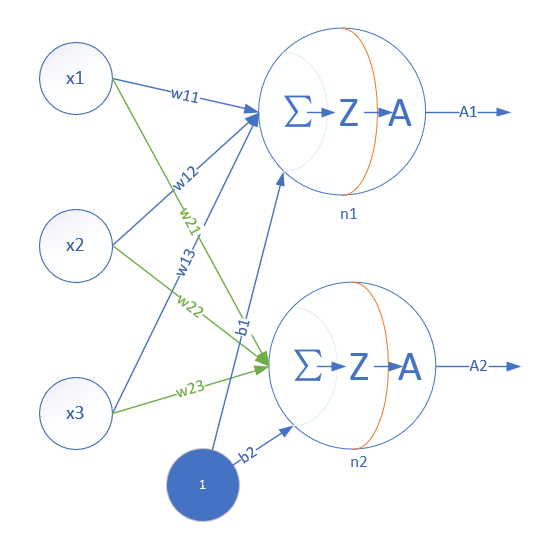
从这里大家可以意识到，同一个特征x1，对于n1、n2来说，权重是不相同的，因为n1、n2是两个神经元，它们完成不同的任务（特征识别）。这就如同老师讲同样的课，不同的学生有不同的理解。

而对于n1来说，x1，x2，x3输入的权重也是不相同的，因为它要对不同特征有选择地接纳。这就如同一个学生上三门课，但是侧重点不同，第一门课花50%的精力，第二门课30%，第三门课20%。

训练流程

从真正的“零”开始学习神经网络时，我没有看到过一个流程图来讲述训练过程，大神们写书或者博客时都忽略了这一点，我在这里给大家画一个简单的流程图：

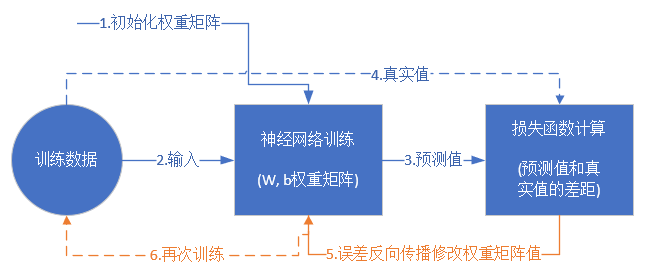
损失函数和反向传播的更多内容在后续的博客中。

前提条件

1. 首先是我们已经有了训练数据，否则连目标都没有，训练个啥？
2. 我们已经根据数据的规模、领域，建立了神经网络的基本结构，比如有几层，每一层有几个神经元
3. 定义好损失函数来合理地计算误差

步骤

假设我们有以下训练数据样本：

Id	x1	x2	x3	Y
1	0.5	1.4	2.7	3
2	0.4	1.3	2.5	5
3	0.1	1.5	2.3	9
4	0.5	1.7	2.9	1

其中，x1，x2，x3是每一个样本数据的三个特征值，Y是样本的真实结果值，

1. 随机初始化权重矩阵，可以根据高斯分布或者正态分布等来初始化。这一步可以叫做“蒙”，但不是瞎蒙。
2. 拿一个或一批数据作为输入，带入权重矩阵中计算，再通过激活函数传入下一层，最终得到预测值。在本例中，我们先用Id-1的数据输入到矩阵中，得到一个A值，假设A=5
3. 拿到Id-1样本的真实值Y=3
4. 计算损失，假设用均方差函数 Loss=(A−Y)2=(5−3)2=4Loss=(A−Y)2=(5−3)2=4
5. 根据一些神奇的数学公式（反向微分），把Loss=4这个值用大喇叭喊话，告诉在前面计算的步骤中，影响A=5这个值的每一个权重矩阵，然后对这些权重矩阵中的值做一个微小的修改（当然是向着好的方向修改，这一点可以用数学家的名誉来保证）
6. 用Id-2样本作为输入再次训练（goto 2）
7. 这样不断地迭代下去，直到以下一个或几个条件满足就停止训练：损失函数值非常小；迭代了指定的次数；

训练完成后，我们会把这个神经网络中的结构和权重矩阵的值导出来，形成一个计算图（就是矩阵运算加上激活函数）模型，然后嵌入到任何可以识别/调用这个模型的应用程序中，根据输入的值进行运算，输出预测值。

神经网络为什么能普遍适用

单层的神经网络能够模拟一条二维平面上的直线，从而可以完成线性分割任务。而理论证明，两层神经网络可以无限逼近任意连续函数。

比如下面这张图，二维平面中有两类点，红色的和蓝色的，用一条直线肯定不能把两者分开了。

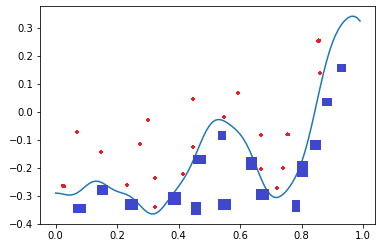
我们使用一个两层的神经网络可以得到一个非常近似的结果，使得分类误差在满意的范围之内。而这个真实的连续函数的原型是：

y=0.4x2+0.3xsin(15x)+0.01cos(50x)−0.3

哦，my god（我靠）! 这么复杂的函数，一个两层的神经网络是如何做到的呢？其实从输入层到隐藏层的矩阵计算，就是对输入数据进行了空间变换，使其可以被线性可分，然后输出层画出了一个分界线。而训练的过程，就是确定那个空间变换矩阵的过程。因此，多层神经网络的本质就是对复杂函数的拟合。我们可以在后面的试验中来学习如何拟合上述的复杂函数的。

为什么需要激活函数

为什么我们不能在没有激活输入信号的情况下完成神经网络的学习呢？

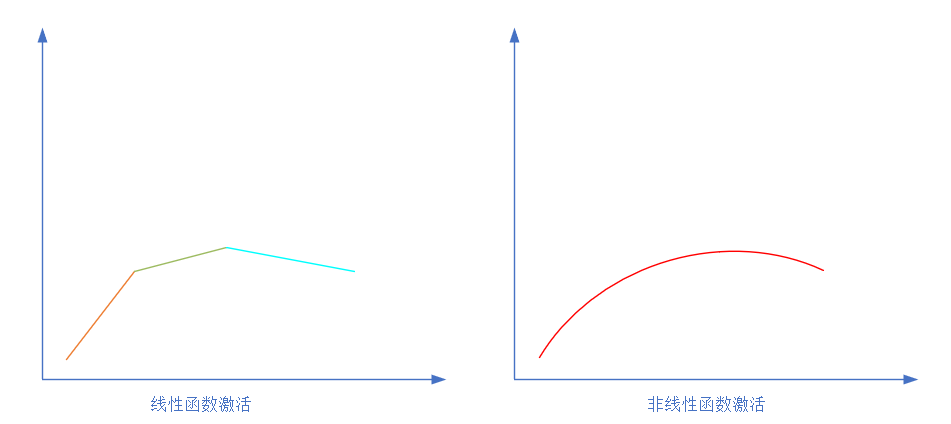
如果我们不运用激活函数的话，则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式。现如今，线性方程是很容易解决的，但是它们的复杂性有限，并且从数据中学习复杂函数映射的能力更小。一个没有激活函数的神经网络将只不过是一个线性回归模型（Linear regression Model）罢了，它功率有限，并且大多数情况下执行得并不好。我们希望我们的神经网络不仅仅可以学习和计算线性函数，而且还要比这复杂得多。同样是因为没有激活函数，我们的神经网络将无法学习和模拟其他复杂类型的数据，例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术，诸如深度学习（Deep learning），来理解一些复杂的事情，一些相互之间具有很多隐藏层的非线性问题，而这也可以帮助我们了解复杂的数据。

那么为什么我们需要非线性函数？

非线性函数是那些一级以上的函数，而且当绘制非线性函数时它们具有曲率。现在我们需要一个可以学习和表示几乎任何东西的神经网络模型，以及可以将输入映射到输出的任意复杂函数。神经网络被认为是通用函数近似器（Universal Function Approximators）。这意味着他们可以计算和学习任何函数。几乎我们可以想到的任何过程都可以表示为神经网络中的函数计算。
而这一切都归结于这一点，我们需要应用激活函数f（x），以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。因此，使用非线性激活函数，我们便能够从输入输出之间生成非线性映射。
激活函数的另一个重要特征是：它应该是可以区分的。我们需要这样做，以便在网络中向后推进以计算相对于权重的误差（丢失）梯度时执行反向优化策略，然后相应地使用梯度下降或任何其他优化技术优化权重以减少误差。

深度神经网络与深度学习

两层的神经网络虽然强大，但可能只能完成二维空间上的一些曲线拟合的事情。如果对于图片、语音、文字序列这些复杂的事情，就需要更复杂的网络来理解和处理。第一个方式是增加每一层中神经元的数量，但这是线性的，不够有效。另外一个方式是增加层的数量，每一层都处理不同的事情。

浅神经网络虽然具备了反向传播机制，但是仍存在问题：

1. 梯度越来越疏，从后向前，误差校正信号越来越微弱
2. 随机初始化会导致训练过程收敛到局部最小值
3. 需要数据带标签(人工label好的数据)，但是大部分数据没标签