平衡树、AVL树

平衡树

平衡树有AVL树、红黑树、2-3树、2-3-4树

AVL树

AVL树是最早的一种平衡树，它以发明者的名字命名；AVL是一种特殊的二叉搜索树，平移保证二叉搜索树的正确。

特征

在AVL树中节点的左子树和右子树的高度差不会大于1

实现

在AVL树中每个节点都存储着一个额外的数据，它的左子树和右子树的高度差，这个差值不能大于1。
插入一个元素后，检查该元素所在的最低子树的根，如果它的子节点的高度相差大于1，执行一次或两次旋转使它们的高度相等；然后接着检查上面的节点，必要时均衡高度；这个检测一直向上，直到根为止。

旋转

右旋，顶端节点必须有一个左子节点，否则将没有节点代替原来的顶端节点；反之亦然。只要一个节点的左边有很多子孙节点而右边没有这么多节点，右旋；反之亦然。

1、单旋转——右旋1

a图是一个正确的AVL树，节点50的右子树高度为0，左子树的高度为1，差值不大于1
b图插入一个节点30后，整个树不平衡了。右旋，以节点50为顶端节点做右旋，节点50下降，节点40上升，节点30跟随着上升
c图是旋转后的样子

2、单旋转——右旋2

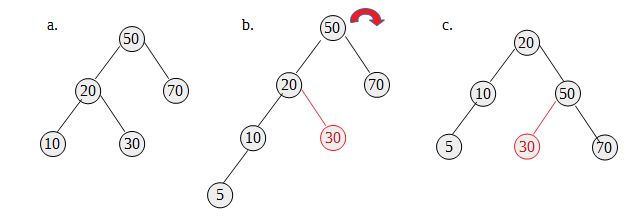
a图是一个正确的AVL树，节点50的右子树高度为1，左子树的高度为2，差值不大于1
b图插入一个节点5后，整个树不平衡了。右旋，以节点50为顶端节点做右旋，节点50下降，节点70跟随着下降；节点20上升，节点10、节点5跟随着上升；但节点30要平移
c图是旋转后的样子
注意：顶端节点的内侧子孙要做平移。如果顶端节点的内侧子孙是一颗树，旋转不会改变该子树中节点的关系，整体跟着平移就好了。

3、双旋转——左-右双旋转

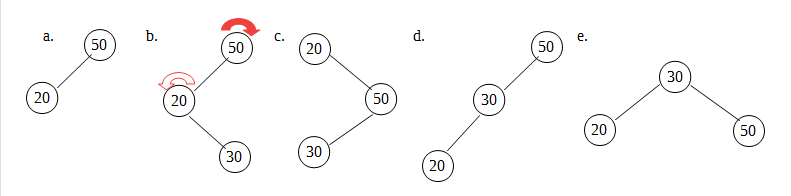
a图是一个正确的AVL树，节点50的右子树高度为0，左子树的高度为1，差值不大于1
b图插入一个节点30后，整个树不平衡了。
c假如对b图做右旋，以节点50为顶端节点做右旋，节点50下降；节点20上升；但节点30要平移——这样就产生了c图，但c图还是不平衡，所以不能这么做
d正确的做法是，对b图以节点20做为顶端节点先做一次左旋，这次左旋后的样子如d图，还不平衡；
e再右旋，以节点50为顶端节点做右旋，结果如e图

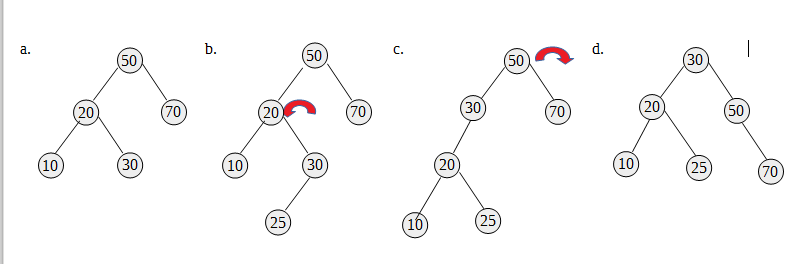
a图是一个正确的AVL树，节点50的右子树高度为1，左子树的高度为2，差值不大于1
b图插入一个节点25后，整个树不平衡了。先左旋，以节点20为顶端节点做左旋，节点20下降，节点10跟随着下降；节点30上升；但节点25要平移
c图是第一次左旋后的样子，还不平衡；再右旋，以节点50为顶端节点做右旋
d图是旋转好的样子
注意：当新节点添加到内侧时，要做两次旋转；当新节点添加到了外侧时，只做一次旋转即可，如右旋1和右旋2

旋转总结

左-右双旋转举了两个例子。以上三种旋转包含了所有的旋转，只是对应的还有左旋、左旋2、右-左双旋转。

效率

AVL树的层数最多是Log₂(N+1)+1，查找时间最差需要Log₂(N+1)+1次比较，大约O(logN)。

插入或删除也大约需要O(logN)的时间。插入或删除一个节点时需要扫描两趟，一次向下查找插入点，一次向上平衡树，所以不如红黑树效率高。