中山纪中集训Day5叒是测试（划淼）

A组T1 矩阵游戏(game) 九校联考24OI__D1T1

问题描述

LZK发明一个矩阵游戏，大家一起来玩玩吧，有一个N行M列的矩阵。第一行的数字是1,2,…M,第二行的数字是M+1,M+2…2*M,以此类推，第N行的数字是(N-1)*M+1,(N-1)*M+2…N*M。
例如,N=3,M=4的矩阵是这样的:
1 2 3 4
5 6 7 8
9 10 11 12

对于身为智慧之神的LZK来说,这个矩阵过于无趣.于是他决定改造这个矩阵,改造会进行K次,每次改造会将矩阵的某一行或某一列乘上一个数字,你的任务是计算最终这个矩阵内所有数字的和,输出答案对109+7取模。

输入

第一行包含三个正整数N、M、K，表示矩阵的大小与改造次数。接下来的行,每行会是如下两种形式之一:
R X Y,表示将矩阵的第X(1 ≤ X ≤ N)行变为原来的Y(0 ≤ Y ≤10^9)倍.
S X Y,表示将矩阵的第X(1 ≤ X ≤ M)列变为原来的Y(00≤ Y ≤10^9)倍.

输出

输出一行一个整数,表示最终矩阵内所有元素的和对109+7109+7取模的结果。

输入输出样例

样例1

input
3 4 4
R 2 4
S 4 1
R 3 2
R 2 0
output
94

样例2

input
2 4 4
S 2 0
S 2 3
R 1 5
S 1 3
output
80

样例一的解释:操作结束之后矩阵会变成这样:
1 2 3 4
0 0 0 0
18 20 22 24

数据范围

40%的数据满足：1≤N,M≤1000；
80%的数据满足：1≤N,M≤1000000,1 ≤ K ≤1000；
100%的数据满足：1≤N,M≤1000000,1 ≤ K ≤100000。

假装很酷地分析

暗中观察可知

1.操作可以任意顺序进行，不会影响最终结果。

2.每一行都是一个等差数列，且一开始公差都为1。

3.每一列相加得到的数列也是等差数列，公差为所有等差数列的公差之和。

我们就可以考虑先进行 行 的操作，再进行 列 的操作。每一行的数乘上一个数后仍然是等差数列，公差增加相应倍数。这样，对于每一行，我们只用维护第一项和它的公差就好了。当 行的操作弄完后，将所有等差数列的第一项相加，得到第一列的和，再将公差相加，得到每一列和的公差，就可以求出每一列的和，剩下的就是直接对列的和进行乘法就好了。（终于帅气地切掉一道题的激动）

#include<cstdio>
const int mod=;
int n,m,k,cnt;char ch[];
int a[],b[],sum[],d,ans;
struct node{int x,y;}q[];
int main()
{
    //freopen("game.in","r",stdin);freopen("game.out","w",stdout);
    scanf("%d%d%d",&n,&m,&k);for(int i=;i<=n;i++)a[i]=(1ll*(i-)*m+)%mod,b[i]=;
    for(int i=,x,y;i<=k;i++)
    {
        scanf("%s%d%d",ch+,&x,&y);
        if(ch[]=='S'){q[++cnt].x=x,q[cnt].y=y;continue;}
        a[x]=(1ll*a[x]*y)%mod;b[x]=(1ll*b[x]*y)%mod;
    }
    for(int i=;i<=n;i++)sum[]=(sum[]+a[i])%mod,d=(d+b[i])%mod;
    for(int i=;i<=m;i++)sum[i]=(sum[i-]+d)%mod;
    for(int i=;i<=cnt;i++)sum[q[i].x]=(1ll*sum[q[i].x]*q[i].y)%mod;
    for(int i=;i<=m;i++)ans=(ans+sum[i])%mod;
    printf("%d\n",ans);
}

A组T2 跳房子（jump）跳楼

↑

导致我几天更不了博客的万恶之源

题目描述

跳房子，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一。
跳房子是在N个格子上进行的，CYJ对游戏进行了改进，该成了跳棋盘，改进后的游戏是在一个N行M列的棋盘上进行，并规定从第一行往上可以走到最后一行，第一列往左可以走到最后一列，反之亦然。每个格子上有一个数字。
在这个棋盘左上角(1,1)放置着一枚棋子。每次棋子会走到右、右上和右下三个方向格子中对应上数字最大一个。即任意时刻棋子都只有一种走法，不存在多个格子同时满足条件。
现在有两种操作：
move k将棋子前进k步。
change a b e将第a行第b列格子上的数字修改为e。
请对于每一个move操作输出棋子移动完毕后所处的位置。

输入格式

第一行包含两个正整数N,M，表示棋盘的大小。
接下来N行，每行M个整数，依次表示每个格子中的数字a[i,j]。
接下来一行包含一个正整数Q，表示操作次数。
接下来m行，每行一个操作。

输出格式

对于每个move操作，输出一行两个正整数x,y，即棋子所处的行号和列号。

样例

样例输入

4 4
1 2 9 3
3 5 4 8
4 3 2 7
5 8 1 6
4
move 1
move 1
change 1 4 100
move 1

样例输出

4 2
1 3
1 4

数据范围与提示

10的数据满足：3⩽N,M⩽50，Q⩽5,000，k⩽50；
20的数据满足：3⩽N,M⩽200，Q⩽5,000，k⩽5,000；
另有20的数据满足：3⩽N,M⩽200，Q⩽5,000，k⩽10^9；
100的数据满足：3⩽N,M⩽2,000，Q⩽5,000，e,k⩽10^9；

看完题解才知道如何分析

首先，图中肯定有环。但如果选择维护所有点是否在环上，一次更改操作复杂度就爆炸了。（于是考场上我选择一步一步走）其实只需要选一个折中的办法，维护第一列的每个点走n步回到第一列会到达哪个位置，以及第一列每个点是否在环上和环的长度即可（这是个基环树，只会有一个环）。

对于每次移动操作，先暴力移动到第一列，再一行一行的跳，若跳到环则直接让 步数 模 环的长度，最后仍然一次跳一行，步数不足一行就暴力跳。

对于每次修改操作，先判断修改的点的前面三个点中，哪些是会因为它的改变而改变路径，在倒退看第一列哪些点会经过这三个点，修改要维护的信息。

修改时每个点都倒退回去显然是会TLE的，但我们发现两个相邻的点路径无法交叉，就像这样：

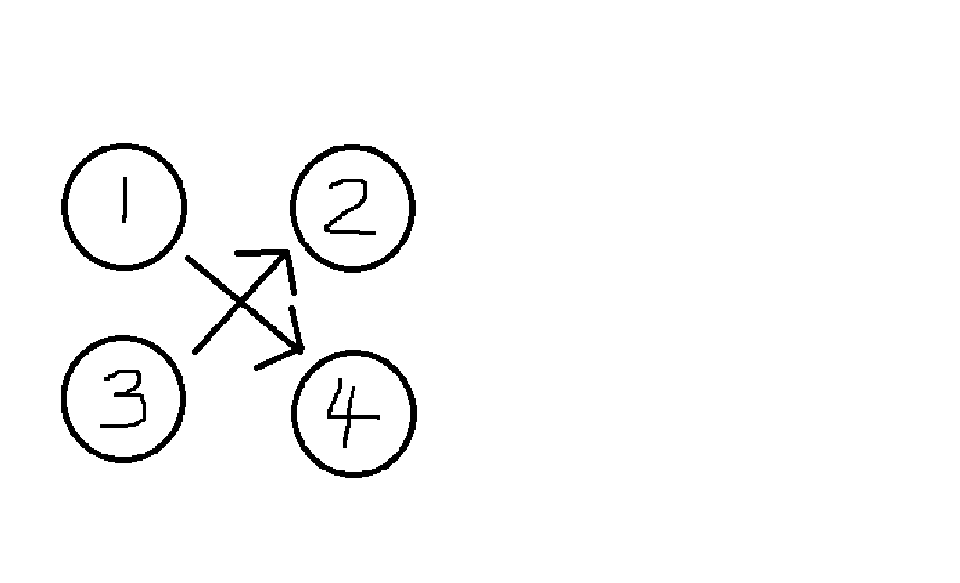
显然这样的情况是不合法的。既然路径无法交叉，我们就只用维护受影响的点中两边上的几个点，就可以得到受影响的点的左右边界。（因为移动可能会越过边界，所以左边界可能比右边界还要大，这时维护矩阵两侧的点就好了）。讲得比我详细不知多少倍的原博客：https://www.cnblogs.com/wzc521/p/11310817.html。

代码（这道题写的我想去跳楼了，所以不要在意那个O2）

#pragma GCC optimize(2)
#include<cstdio>
int n,m,q,len,dx[]={-,,};char ch[];
int cir[],vis[],sta[],inst[],jump[],mart[][];
struct node{int x,y;}ans,p[];
inline node nex(node o)
{
    int maxx=,nex,y=o.y%m+;
    for(int k=,x;k<;k++)if(mart[x=(o.x+dx[k]-+n)%n+][y]>maxx)maxx=mart[nex=x][y];
    return (node){nex,y};
}
inline node walk(node o,int k){if(!k)return o;return walk(nex(o),k-);}
inline void judge(int x)
{
    vis[x]=inst[x]=;sta[++sta[]]=x;
    if(inst[jump[x]])
    {
        int y;len=;
        do{inst[y=sta[sta[]--]]=;cir[y]=;len+=m;}while(y!=jump[x]);
    }
    else if(!vis[jump[x]])judge(jump[x]);
    inst[x]=;
}
inline void move(int k)
{
    while(k&&ans.y!=)k--,ans=nex(ans);
    while(k>=m&&!cir[ans.x])k-=m,ans.x=jump[ans.x];
    k%=len;while(k>=m)k-=m,ans.x=jump[ans.x];
    while(k--)ans=nex(ans);
}
inline int fix(int x,int y,int k1)
{
    if(y==)return x;int befx=-;
    node bef;bef.y=(y--+m)%m+;
    for(int k=;k<=&&befx==-;k++)
    bef.x=(x+k1*dx[k]-+n)%n+,befx=nex(bef).x==x&&nex(bef).y==y?fix(bef.x,bef.y,k1):-;
    return befx;
}
inline void change(int a,int b,int e)
{
    int v[][]={},y=(b--+m)%m+;
    for(int k=;k<;k++)p[k].x=(a-dx[k]-+n)%n+,p[k].y=y,v[k][]=(nex(p[k]).x==a&&nex(p[k]).y==b);
    mart[a][b]=e;for(int k=;k<;k++)v[k][]=(nex(p[k]).x==a&&nex(p[k]).y==b);
    for(int k=,tot;k<;k++)if(v[k][]!=v[k][])
    {
        tot=walk(p[k],m-p[k].y+).x;
        int l=fix(p[k].x,p[k].y,),r=fix(p[k].x,p[k].y,-);
        if(l==-||r==-)continue;
        for(int i=l;i!=r;i=i%n+)jump[i]=tot;jump[r]=tot;
    }
}
int main()
{
    //freopen("jump.in","r",stdin);freopen("jump.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)for(int j=;j<=m;j++)scanf("%d",&mart[i][j]);
    for(int i=;i<=n;i++)jump[i]=walk((node){i,},m).x;
    for(int i=;i<=n;i++)if(!vis[i])judge(i);
    scanf("%d",&q);ans.x=ans.y=;
    while(q--)
    {
        scanf("%s",ch);
        if(ch[]=='m')
        {
            int k;scanf("%d",&k);
            move(k);
            printf("%d %d\n",ans.x,ans.y);
        }
        else
        {
            int a,b,e;scanf("%d%d%d",&a,&b,&e);
            change(a,b,e);
            for(int i=;i<=n;i++)vis[i]=cir[i]=;
            sta[]=;
            for(int i=;i<=n;i++)if(!vis[i])judge(i);
        }
    }
}

A组T3 优美序列(sequence)

问题描述

Lxy养了N头奶牛，他把N头奶牛用1..N编号，第i头奶牛编号为i。为了让奶牛多产奶，每天早上他都会让奶牛们排成一排做早操。奶牛们是随机排列的。在奶牛排列中，如果一段区间[L,R]中的数从小到大排列后是连续的，他认为这段区间是优美的。比如奶牛排列为：(3, 1, 7, 5, 6, 4, 2)，区间[3,6]是优美的，它包含4,5,6,7连续的四个数，而区间[1,3] 是不优美的。Lxy的问题是：对于给定的一个区间[L,R]（1<=L<=R<=N）, 他想知道，包含区间[L,R]的最短优美区间，比如区间[1,3]的最短优美区间是[1,7]。

输入

第一行为一个整数N，表示奶牛的个数。
第二行为1到N的一个排列，表示奶牛的队伍。
第三行为一个整数M，表示有M个询问。
后面有M行，每行有两个整数L,R表示询问区间。

输出

输出为M行，每行两个整数，表示包含询问区间的最短优美区间。

输入输出样例

样例1

input
7
3 1 7 5 6 4 2
3
3 6
7 7
1 3
output
3 6
7 7
1 7

样例2

input
10
2 1 4 3 5 6 7 10 8 9
5
2 3
3 7
4 7
4 8
7 8
output
1 4
3 7
3 7
3 10
7 10

数据范围

15%的数据满足: 1 <=N,M <= 15；
50%的数据满足：1 <=N,M <= 1000。
100%的数据满足：1 <=N,M <= 100000。

根本不是正解的分析

在一个大佬的博客看到了80分的算法：（原博客：https://www.cnblogs.com/Ch-someone/p/9664616.html）

“

     解析

为了给出题人留面子，不让他被骂出个题只有一种解法而且只有满分解法，我先给个80分做法。
      预处理一个数组pos[i]，表示数i在原数组的位置(第几个数)。
      在询问区间内找一个最小值和最大值，作为新的l和r，新的l和r作为一个询问区间，在pos数组里找一个最小值和最大值，他们再作为新的l和r，形成询问区间，在原数组寻找最小值和最大          值，并再次重复刚才的操作……
      上述过程可能很无脑很中二，然而这就是模拟题意找出答案的过程。
      最大值最小值用st表预处理，一共四个st表，比线段树好写……
      那么…… 
      正解是分治，像归并排序那样。
      不断求[l,mid] [mid+1,r]的优美序列，直到分成[mid,mid+1]
      可以证明是正确的。
      事实上分治做的熟练的人可能一眼秒这道题。

”

于是，某个同学把这个80分解法拿过来加了个优化，然后就过了。。。。。

优化是这样的：对于任意一个区间（l,r），它的最短优美区间一定包含它子区间的最短优美区间，所以用一个st表预处理以i为左端点，长度为2^j的区间的最短优美区间即可。

代码：

#include<cstdio>
#include<algorithm>
const int maxn=2e5+;
using namespace std;
struct node{int x,y;node(int x=,int y=):x(x),y(y){}}ans,pre[maxn][];
int n,m,a[maxn],log[maxn],pos[maxn];
int mx[maxn][],mn[maxn][],mxp[maxn][],mnp[maxn][];
inline void print(int x){if(x>)print(x/);putchar(x%+);}
inline int read(){register int x=;char ch;while(ch<''||ch>'')ch=getchar();while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}return x;}
inline node solve(int l,int r)
{
    int minn,maxx,k,k1;k=log[r-l+];
    while((maxx=max(mx[l][k],mx[r-(<<k)+][k]))-(minn=min(mn[l][k],mn[r-(<<k)+][k]))!=r-l)
    k1=log[maxx-minn+],l=min(mnp[minn][k1],mnp[maxx-(<<k1)+][k1]),
    r=max(mxp[minn][k1],mxp[maxx-(<<k1)+][k1]),k=log[r-l+];
    return node(l,r);
}
void prework()
{
    for(int i=;i<=n;i++)pre[i][]=node(i,i);
    for(register int i=;i<=log[n];i++)for(register int j=;j<=n&&j+(<<(i-))<=n;j++)
    pre[j][i]=solve(min(pre[j][i-].x,pre[j+(<<(i-))][i-].x),max(pre[j][i-].y,pre[j+(<<(i-))][i-].y));
}
int main()
{
    //freopen("sequence.in","r",stdin);freopen("sequence.out","w",stdout);
    scanf("%d",&n);
    for(register int i=;i<=n;i++)a[i]=read(),mxp[a[i]][]=mnp[a[i]][]=pos[mn[i][]=mx[i][]=a[i]]=i,log[i+]=log[(i+)/]+;;
    for(register int i=;i<=log[n];i++)for(register int j=;j<=n&&j+(<<(i-))<=n;j++)
    mn[j][i]=min(mn[j][i-],mn[j+(<<(i-))][i-]),mx[j][i]=max(mx[j][i-],mx[j+(<<(i-))][i-]),
    mnp[j][i]=min(mnp[j][i-],mnp[j+(<<(i-))][i-]),mxp[j][i]=max(mxp[j][i-],mxp[j+(<<(i-))][i-]);
    prework();
    scanf("%d",&m);
    for(register int i=,l,r,k;i<=m;i++)
    {
        l=read(),r=read(),k=log[r-l+];
        ans=solve(min(pre[l][k].x,pre[r-(<<k)+][k].x),max(pre[r-(<<k)+][k].y,pre[l][k].y));
        print(ans.x);putchar(' ');print(ans.y);puts("");
    }
}