[LeetCode] 62. 不同路径 ☆☆☆(动态规划)

动态规划该如何优化

描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

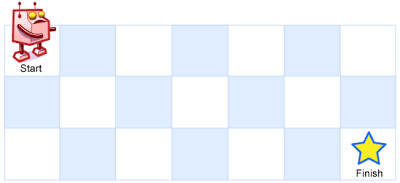
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

解析

应该是很明显的DP算法了。到达右下角的路径数有2个部分：右下角左边的路径数 + 左下角上边的路径数。

即dp[m][n] = dp[m][n - 1] + dp[m - 1][n]。(m行 n列)

边界值，第一行、第一列都为1，因为只有1种走法。

代码

public int uniquePaths(int m, int n) {
        if (m <= 0 || n <= 0) {
            return 0;
        }
        int[][] array = new int[m][n];
        for (int i = 0; i < m; i++) {
            array[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            array[0][i] = 1;
        }
        for (int ii = 1; ii < m; ii++) {
            for (int kk = 1; kk < n; kk++) {
                array[ii][kk] = array[ii - 1][kk] + array[ii][kk - 1];
            }
        }
        return array[m - 1][n - 1];
    }

优化：画图后发现（动归要多画图），其实每次计算都只用了当前行和上一行。可以将二维数组变为一维数组。

dp[m][n] = dp[m][n - 1] + dp[m - 1][n]，可以变为dp[i] = dp[i] + dp[i -  1]

public static int uniquePaths1(int m, int n) {
        if (m <= 0 || n <= 0) {
            return 0;
        }
        int[] dp = new int[n];// 用列初始化
        // 初始化
        for (int i = 0; i < n; i++) {
            dp[i] = 1;
        }
        // 公式：dp[i] = dp[i-1] + dp[i]
        for (int i = 1; i < m; i++) {//还是需要双层循环的，画图即知 比如m = 3, n = 2
            dp[0] = 1; // 第 i 行第 0 列的初始值
            for (int j = 1; j < n; j++) {
                dp[j] = dp[j - 1] + dp[j];
            }
        }
        return dp[n - 1];
    }