Deep Learning专栏--强化学习之MDP、Bellman方程（1）

本文主要介绍强化学习的一些基本概念：包括MDP、Bellman方程等, 并且讲述了如何从 MDP 过渡到 Reinforcement Learning。

1. 强化学习基本概念

这里还是放上David Silver的课程的图，可以很清楚的看到整个交互过程。这就是人与环境交互的一种模型化表示，在每个时间点，大脑agent会从可以选择的动作集合A中选择一个动作$a_t$执行。环境则根据agent的动作给agent反馈一个reward $r_t$，同时agent进入一个新的状态。

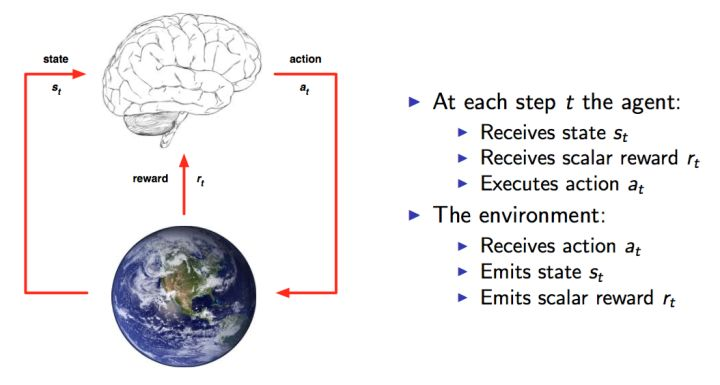
根据上图的流程，任务的目标就出来了，那就是要能获取尽可能多的Reward。Reward越多，就表示执行得越好。每个时间片，agent根据当前的状态来确定下一步的动作。也就是说我们需要一个state找出一个action，使得reward最大，从 state 到 action 的过程就称之为一个策略Policy，一般用$\pi $表示。

强化学习的任务就是找到一个最优的策略Policy从而使Reward最多。

在运行强化学习算法之前，首先需要得到一系列的状态,动作和反馈，这个过程通常是agent随机得到的：

$$ (s_1,a_1,r_1,s_2,a_2,r_2,…s_t,a_t,r_t) $$

这就是一系列的样本Sample。强化学习的算法就是需要根据这些样本来改进Policy，从而使得得到的样本中的Reward更好。

由于这种让Reward越来越好的特性，所以这种算法就叫做强化学习Reinforcement Learning。

2. MDP（Markov Decision Process）

强化学习的问题都可以模型化为MDP(马尔可夫决策过程)的问题，MDP 实际上是对环境的建模；MDP 与常见的 Markov chains 的区别是加入了action 和 rewards 的概念。

因此，一个基本的 MDP 可以用一个五元组$(S,A,P,R, \gamma)$表示，其中:

1. $S$是一个有限状态集；
2. $A$是一个有限动作集；
3. $P$是一个状态转移概率矩阵，$P_a(s, s′)=P(s_{t+1}=s′|s_t=s, a_t=a)$表示在状态$s$下执行动作$a$后转移到状态 $s′$的概率；
4. $R$是一个奖励函数，$R_a(s, s′)$ 表示在状态 $s$ 下执行动作 $a$ 后转移到状态 $s′$ 所得到的即时回报(reward)；
5. $\gamma$是一个折扣因子,一般取值在 [0,1]；用来区分当前回报和未来回报的重要性，一般会加在未来的回报前，减小未来回报的权重。

因此，MDP 的核心问题就是找到一个策略 $\pi(s)$ 来决定在状态 $s$ 下选择哪个动作，这种情况下MDP就变成了一个 Markov chain，且此时的目标跟我们前面提到的强化学习的目标是一致的。

3. 回报与价值函数

状态的好坏等价于对未来回报的期望。因此，引入回报(Return) 来表示某个时刻$t$的状态将具备的回报：

$$ G_t = R_{t+1} + \gamma R_{t+2} + … = \sum_{k=0}^\infty\gamma^kR_{t+k+1} $$

上面 $R$ 是 Reward 反馈，$\gamma$ 是 discount factor（折扣因子）,跟前面 MDP 中的符号的含义一致。

从上面的式子可以， 除非整个过程结束，否则我们无法获取所有的 reward 来计算出每个状态的 Return，因此，再引入一个概念:价值函数(value function),记为 $V(s)$，通过 $V(s)$ 来表示一个状态未来的潜在价值。从定义上看，value function 就是回报的期望：

$$ V(s) = \mathbb E[G_t|S_t = s] $$

引出价值函数，对于获取最优的策略Policy这个目标，我们就可以通过估计 value function 来间接获得优化的策略。道理很简单，通过价值函数可以知道每一种状态的好坏，这样我们就知道该怎么选择了（如选择动作使得下一状态的潜在价值最大），而这种选择就是我们想要的策略。

我们需要估算 Value Function，只要能够计算出价值函数，那么最优决策也就得到了。因此，问题就变成了如何计算Value Function？

根据前面 $G_t$ 和 $V(s)$ 的定义，有：

$$ \begin{align} V(s) & = \mathbb E[G_t|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma R_{t+2} + \gamma ^2R_{t+3} + …|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma (R_{t+2} + \gamma R_{t+3} + …)|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma G_{t+1}|S_t = s]\\ & = \mathbb E[R_{t+1}+\gamma v(S_{t+1})|S_t = s] \end{align} $$

则有:

$$ V(s) = \mathbb E[R_{t+1} + \gamma V(S_{t+1})|S_t = s] $$

上面这个公式就是Bellman方程的基本形态。从公式上看，当前状态的价值和下一步的价值以及当前的反馈Reward有关, 其中透出的含义就是价值函数的计算可以通过迭代的方式来实现。

4. 从 MDP 到 Reinforcement Learning

回到 MDP 问题，如果我们知道了转移概率 $P$ 和奖励函数 $R$，那么便可通过下面的方法求出最优策略 $\pi(s)$, 首先，结合上面提到的价值函数和Bellman方程有：

公式1：

$$ \pi(s):=\arg \max_a\ {\sum_{s’}P_{a}(s,s’)(R_{a}(s,s’)+\gamma V(s’))} $$

公式2:

$$ V(s) := \sum_{s’}P_{\pi(s)}(s,s’)(R_{\pi(s)}(s,s’) + \gamma V(s’)) $$

公式 1 表示在状态 $s$ 下的采取的最优动作，公式 2 表示在状态 $s$ 下的价值，可以看到两者有依存关系；

而在 转移概率 $P$ 和奖励函数 $R$已知的情况下，求解 MDP 问题常见做法有 Value iteration 或 Policy iteration.

4.1 Value iteration

在 Value iteration 中，策略函数 $\pi$ 没有被使用，迭代公式如下：

$$ V_{i+1}(s) := \max_a \sum_{s’} P_a(s,s’)(R_a(s,s’) + \gamma V_i(s’)) $$

下标 $i$ 表示第 $i$ 次迭代，在每轮迭代中需要计算每个状态的价值，并且直到两次迭代结果的差值小于给定的阈值才能认为是收敛。

计算的出收敛的价值函数后，通过公式1就能够得出策略函数 $\pi$ 了，其迭代过程如下图所示:

4.2 Policy iteration

Policy iteration同时更新价值 $V$ 和策略 $\pi$, 且一般可分成两步：

Policy Evaluation，策略评估，就是上面公式2的过程。目的是在策略固定的情况下更新Value Function 直到 value 收敛，从另一个角度来讲就是为了更好地估计基于当前策略的价值
Policy Improvement，策略改进，就是上面公式1的过程。就是根据更新后的 Value Function 来更新每个状态下的策略直到策略稳定
这个方法本质上就是使用当前策略($\pi$)产生新的样本，然后使用新的样本更好的估计策略的价值($V(s)$)，然后利用策略的价值更新策略，然后不断反复。理论可以证明最终策略将收敛到最优.

具体的算法流程如下所示:

4.3 区别与局限

问题来了，上面的 Policy Iteration 和 Value Iteration有什么区别, 为什么一个叫policy iteration，一个叫value iteration？

原因其实很好理解，policy iteration 最后收敛的 value $V$ 是当前 policy 下的 value 值（也做对policy进行评估），目的是为了后面的policy improvement得到新的policy；所以是在显式地不停迭代 policy。

而value iteration 最后收敛得到的 value 是当前state状态下的最优的value值。当 value 最后收敛，那么最优的policy也就得到的。虽然这个过程中 policy 在也在隐式地更新，但是一直在显式更新的是 value，所以叫value iteration。

从上面的分析看，value iteration 较 之policy iteration更直接。不过问题也都是一样，都需要知道转移概率 $P$ 和奖励函数 $R$。

但是对于 Reinforcement Learning 这一类问题，转移概率 $P$ 往往是不知道，知道转移概率 $P$ 也就称为获得了模型 Model，这种通过模型来获取最优动作的方法也就称为 Model-based 的方法。但是现实情况下，很多问题是很难得到准确的模型的，因此就有 Model-free 的方法来寻找最优的动作，像 Q-learning，Policy Gradient，Actor Critic这一类方法都是 model-free 的。

前面的方法问题是需要已知转移概率 $P$, 目的是为了遍历当前状态后的所有可能的状态，因此如果采用贪婪的思想，那么就不需要不遍历后面所有的状态，而是直接采取价值最大的状态动作来执行。

Q-learning 实际上就是采用这种思想的，Q-Learning的基本思想是根据 value iteration 得到的，但要明确一点是 value iteration 每次都对所有的Q值更新一遍，也就是所有的状态和动作。但事实上在实际情况下我们没办法遍历所有的状态，还有所有的动作，因此，我们只能得到有限的系列样本。具体的算法流程会再下一篇文章具体介绍。

综上，本文主要介绍了强化学习的任务和一些概念，以及从 MDP 如何过渡到 Reinforcement，在后续的文章中会介绍value-based的Q-learning 和DQN方法，Policy gradient 类方法以及结合两者的 Actor Critic 及DDPG方法。

---

参考资料:

1. 吴良超的学习笔记：强化学习笔记(1)-概述

2. DQN 从入门到放弃4 动态规划与Q-Learning