VLAD算法浅析, BOF、FV比较

划重点

=================================================

BOF、FV、VLAD等算法都是基于特征描述算子的特征编码算法，关于特征描述算子是以SIFT为基础的一类算法，该类算法能得到图片的一系列局部特征，该类特征对旋转、缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性，但是该类特征产生的特征矩阵一般都较为庞大，因此需要利用特征编码算法对其进行编码，以便后续构建索引，实现图像检索。

 

BOF、FV、VLAD都需要对SIFT得到的特征进行聚类，得到一个码本，利用码本，将原始的N维特征向量映射到K维的空间中，不同之处在于映射方法不同。

 

BOF（Bag Of Features）：建立码本时采用K-means，在映射时，利用视觉词袋量化图像特征，统计的词频直方图，该词频直方图即为编码后的特征向量，损失的信息较多。BOF是把特征点做kmeans聚类，然后用离特征点最近的一个聚类中心去代替该特征点，损失较多信息；

 

FV（Fisher Vector）：FV是对特征点用GMM建模，GMM实际上也是一种聚类，只不过它是考虑了特征点到每个聚类中心的距离，也就是用所有聚类中心的线性组合去表示该特征点，在GMM建模的过程中也有损失信息。

 

VLAD（vector of locally aggregated descriptors）：VLAD像BOF那样，只考虑离特征点最近的聚类中心，VLAD保存了每个特征点到离它最近的聚类中心的距离； 像Fisher vector那样，VLAD考虑了特征点的每一维的值，对图像局部信息有更细致的刻画； 而且VLAD特征没有损失信息。

=========================================================

VLAD（Vector of Aggragate Locally Descriptor）算法

VLAD算法可以分为如下几步：

1、提取图像的SIFT描述子

2、利用提取到的SIFT描述子（是所有训练图像的SIFT）训练一本码书，训练方法是K-means

3、把一副图像所有的SIFT描述子按照最近邻原则分配到码书上（也即分配到K个聚类中心）

4、对每个聚类中心做残差和（即属于当前聚类中心的所有SIFT减去聚类中心然后求和）

5、对这个残差和做L2归一化，然后拼接成一个K*128的长向量。128是单条SIFT的长度

如果不考虑海量数据的话，这个训练和建库过程已经可以了，直接保存第五步的结果（图像库），然后对查询图像做上述的操作，之后计算和图像库中每一条向量的欧式距离，输出前5个最小距离，既是一次完整的检索过程。

一、简介

　　虽然现在深度学习已经基本统一了图像识别与分类这个江湖，但是我觉得在某些小型数据库上或者小型的算法上常规的如BoW，FV，VLAD，T-Embedding等还是有一定用处的，如果专门做图像检索的不知道这些常规算法也免得有点贻笑大方了。

　　如上所说的这些算法都大同小异，一般都是基于局部特征（如SIFT，SURF）等进行特征编码获得一个关于图像的feature，最后计算feature之间的距离，即使是CNN也是这个过程。下面主要就是介绍一下关于VLAD算法，它主要是得优点就是相比FV计算量较小，相比BoW码书规模很小，并且检索精度较高。

二、VLAD算法

1. 第一步自然是提取局部特征，有了OpenCV这一步就仅仅是函数调用的问题了：

   SurfFeatureDetector detector;
   SurfDescriptorExtractor extractor;
   detector.detect( image_0,  keypoints );
   extractor.compute( image_0,  keypoints, descriptors );

    

   　　如果对特征有什么要求也可以根据OpenCV的源码或者网上的源码进行修改，最终的结果就是提取到了一幅图像的局部特征（还有关于局部特征参数的控制）；

2. 第二步本应是量化的过程，但是在量化之前需要事先训练一本码书，而码书同BoW一样是用K-means算法训练得到的，同样OpenCV里面也集成了这个算法，所以这个过程也再简单不过了：

   kmeans(descriptors, numClusters, labels,
              TermCriteria( CV_TERMCRIT_EPS+CV_TERMCRIT_ITER, , 0.01 ),
              , KMEANS_PP_CENTERS, centers);

    

   　　需要做的就是定义一些参数，如果自己写的话就不清楚了。另外码书的大小从64-256甚至更大不等，理论上码书越大检索精度越高。

3. 第三步就是量化每一幅图像的特征了，其实如果数据库较小，可以直接使用全部图像的特征作训练，然后Kmeans函数中的labels中存储的就是量化的结果：即每一个特征距离那一个聚类中心最近。但是通常训练和量化是分开的，在VLAD算法中使用的是KDTree算法，KDTree算法是一种快速检索算法，OpenCV里同样集成了KDTree算法：

   const int k=, Emax=INT_MAX;<br>KDTree T(centers,false);
   T.findNearest(descriptors_row, k, Emax, idx_t, noArray(), noArray());

    

   　　通过KDTree下的findNearest函数找到与之最近的聚类中心，需要注意的是输入的STL的vector类型，返回的是centers的索引值；

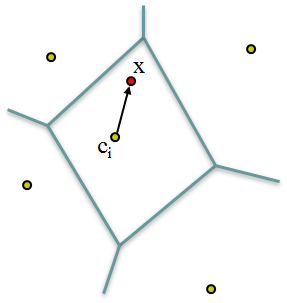
4. 量化结束之后就是计算特征和中心的残差，并对每一幅图像落在同一个聚类中心上的残差进行累加求和，并进行归一化处理，最后每一个聚类中心上都会得到一个残差的累加和，进行归一化时需要注意正负号的问题（针对不同的特征）。假设有k个聚类中心，则每一个聚类中心上都有一个128维（SIFT）残差累加和向量；
5. 把这k个残差累加和串联起来，获得一个超长向量，向量的长度为k*d（d=128），然后对这个超长矢量做一个power normolization处理可以稍微提升检索精度，然后对这个超长矢量再做一次归一化，现在这个超长矢量就可以保存起来了。
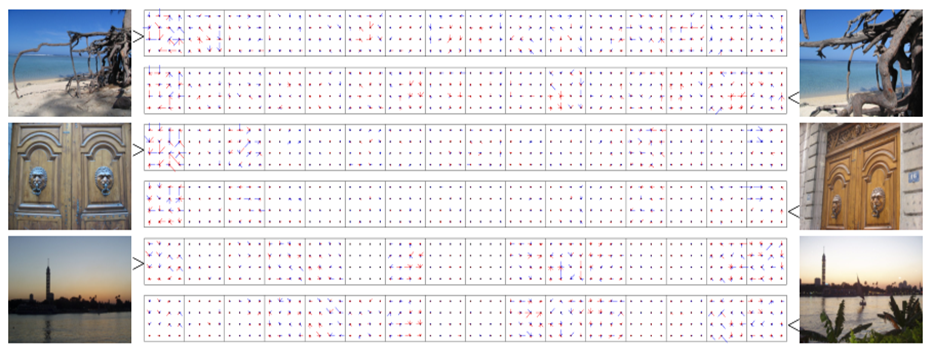
6. 假设对N幅图像都进行了上面的编码处理之后就会得到N个超长矢量，为了加快距离计算的速度通常需要进行PCA降维处理，关于PCA降维的理论同KDTree一样都很成熟，OpenCV也有集成，没有时间自己写就可以调用了：

   PCA pca( vlad, noArray(), CV_PCA_DATA_AS_ROW,  );
   pca.project(vlad,vlad_tt);

    

   　　输入训练矩阵，定义按照行或列进行降维，和降维之后的维度，经过训练之后就可以进行投影处理了，也可以直接调用特征向量进行矩阵乘法运算。这里有一点就是PCA的过程是比较费时的，进行查询的时候由于同样需要进行降维处理，所以可以直接保存投影矩阵（特征值矩阵），也可以把特征向量、特征值、均值都保存下来然后恢复出训练的pca，然后进行pca.project进行投影处理；

7. 如果不考虑速度或者数据库规模不是很大时，就可以直接使用降维后的图像表达矢量进行距离计算了，常用的距离就是欧式距离和余弦距离，这里使用余弦距离速度更快。当然进行距离计算的基础就是已经设计好了训练过程和查询过程。

三、总结

　　可以看到，整个VLAD算法结合OpenCV实现起来还是非常简单的，并且小型数据库上的检索效果还可以，但是当数据库规模很大时只使用这一种检索算法检索效果会出现不可避免的下降。另外在作者的原文中，针对百万甚至千万级的数据库时单单使用PCA降维加速距离的计算仍然是不够的，所以还会使用称之为积量化或乘积量化（Product Quantization）的检索算法进行加速，这个也是一个很有意思的算法，以后有机会再介绍它。

来源： https://www.cnblogs.com/mafuqiang/p/6909556.html

https://blog.csdn.net/u010333076/article/details/87900431

https://blog.csdn.net/zshluckydogs/article/details/81003966