Problem 8 dp

$des$

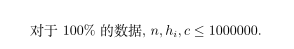
$sol$

记 $f_i$ 表示考虑前 $i$ 个建筑, 并且第 $i$ 个建筑的高度不变的答案, 每次
转移时枚举上一个不变的建筑编号, 中间的一段一定变成相同的高度, 并且
高度小于等于两端的高度.
假设从 $f_j$ 转移且中间高度为 $t$, 则:
$$f_i = \sum_{k = j + 1} ^ {i - 1} (t - h_k) ^ 2 + c(h_j + h_i - 2t)$$
这样中间的高度可以 $O(1)$ 求二次函数的对称轴确定. 考虑优化转移,
因为中间高度要小于两端, 所以最多只有一个 $h_j > h_i$ 的 $j$ 能够转移. 可以
维护关于高度的单调栈, 这样有效的转移次数就是 O(n) 的.

$code$

#include <bits/stdc++.h>

using std::pair;
using std::vector;
using std::string;

typedef long long ll;
typedef pair<int, int> pii;

#define fst first
#define snd second
#define pb(a) push_back(a)
#define mp(a, b) std::make_pair(a, b)
#define debug(...) fprintf(stderr, __VA_ARGS__)

template <typename T> bool chkmax(T& a, T b) { return a < b ? a = b,  : ; }
template <typename T> bool chkmin(T& a, T b) { return a > b ? a = b,  : ; }

template <typename T> T read(T& x) {
    int f = ; x = ;
    char ch = getchar();
    for(;!isdigit(ch); ch = getchar()) if(ch == '-') f = -;
    for(; isdigit(ch); ch = getchar()) x = x *  + ch - ;
    return x *= f;
}

const int N = ;

int n, C;
int h[N + ];
ll s[][N + ], dp[N + ];

ll solve(int x, int y, int mx) {
    ll a = y - x - ;
    ll b = - * (s[][y-] - s[][x]) - (x != ) * C - (y != n+) * C;
    ll c = s[][y-] - s[][x] + 1ll * (x != ) * h[x] * C + 1ll * (y != n+) * h[y] * C;

    ll t;
    t = (ll) ((- b /  / a) + 0.5);

    chkmax<ll>(t, mx);
    if(x != ) chkmin(t, (ll) h[x]);
    if(y <= n) chkmin(t, (ll) h[y]);

    return a * t * t + b * t + c;
}

int main() {

    read(n), read(C);
    for(int i = ; i <= n; ++i) {
        read(h[i]);
        s[][i] = s[][i-] + h[i];
        s[][i] = s[][i-] + 1ll * h[i] * h[i];
    }

    static int stk[N + ], top;

    h[] = h[n + ] = ( << );
    stk[top ++] = ;

    for(int i = ; i <= n+; ++i) {
        dp[i] = dp[i-] + ((i ==  || i == n+) ?  : 1ll * C * std::abs(h[i] - h[i-]));
        while(top >  && h[stk[top-]] <= h[i]) {
            if(top > )
                chkmin(dp[i], dp[stk[top-]] + solve(stk[top-], i, h[stk[top-]]));
            -- top;
        }
        stk[top ++] = i;
    }
    printf("%lld\n", dp[n + ]);

    return ;
}