planning algorithms chapter 3

chapter 3 几何表示和变换

P.S： 总算到了 motion planning 部分了

几何建模

几何建模主要有两类方法：边界表示法和实体表示法。
环境模型可以是二维或三维，实体主要包括障碍物和机器人。

多边形和多面体模型

凸边形定义：子集 $ X \subset \mathbb{R}^{n} $ 为凸集，当且仅当， X 中任意两点连线上的所有点也属于 X 。

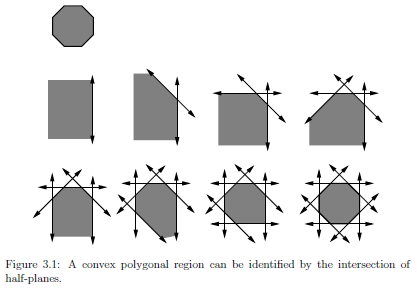
边界表示法可以用多边形表示，用一系列的边界点\(\left ( x_{1}, y_{1} \right ),\left ( x_{2}, y_{2} \right ),\cdots ,\left ( x_{m}, y_{m} \right )\)表示。实体表示法可以用半平面的交集表示。

半平面可以表示如下：
\(H_{i} = \left \{ \left ( x,y \right )\in W| f_{i}\left ( x,y \right )\leqslant 0\right \}.\)

刚体变换

2D 变换

旋转：

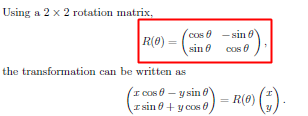
旋转 + 移动：

3D 变换

yaw, pitch, roll：

旋转变换：

反解旋转角：

利用 atan2 可以得到：

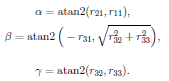
均质变换矩阵(The homogeneous transformation matrix)：

刚体运动链的变化

相互依附的刚体的变化更加复杂，一系列依附的刚体被称为联动，如果刚体通过单链关联，这种联动是运动链。

2D 运动链的均质变换：

3D 运动链的均质变换：
图示：

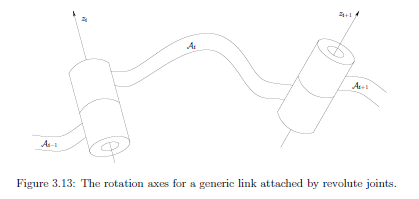
均质变换矩阵：

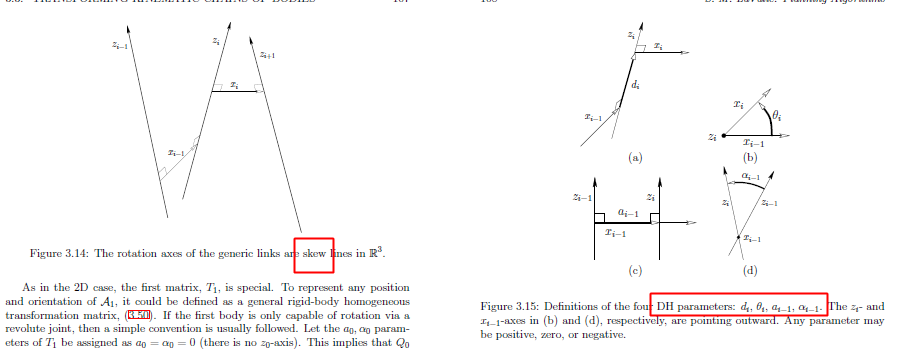
均质变换矩阵的 DH 参数

非刚体变换

线性变换：
旋转变换是一种特殊的线性变换。
同比例放大缩小：

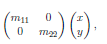
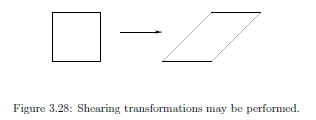
剪切变换：

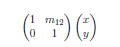
当 m12 = 1 时，剪切变换效果如下图：