(简单) POJ 2750 Potted Flower，环+线段树。

Description

The little cat takes over the management of a new park. There is a large circular statue in the center of the park, surrounded by N pots of flowers. Each potted flower will be assigned to an integer number (possibly negative) denoting how attractive it is. See the following graph as an example:

(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.)

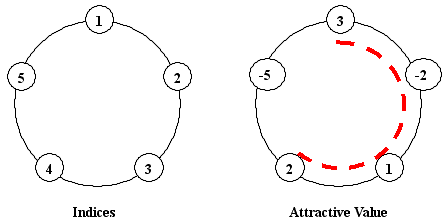
The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among all possible constructions.

Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction.

 

　　题目就是求最大连续和，限制条件是环状和不能全选。

　　一般环状问题是复制一个一样的序列让两个合并，但是这个题这样好像不能做，所以卡了，后来才明白可以维护最小值，来解决环状最大值问题。

 

代码如下：

// ━━━━━━神兽出没━━━━━━
// 　　 ┏┓       ┏┓
// 　　┏┛┻━━━━━━━┛┻┓
// 　　┃           ┃
// 　　┃     ━     ┃
//     ████━████   ┃
// 　　┃           ┃
// 　　┃    ┻      ┃
// 　　┃           ┃
// 　　┗━┓       ┏━┛
// 　　  ┃       ┃
// 　　  ┃       ┃
// 　　　┃       ┗━━━┓
// 　　　┃           ┣┓
// 　　　┃           ┏┛
// 　　　┗┓┓┏━━━━━┳┓┏┛
// 　　　 ┃┫┫     ┃┫┫
// 　　　 ┗┻┛     ┗┻┛
//
// ━━━━━━感觉萌萌哒━━━━━━

// Author        : WhyWhy
// Created Time  : 2015年07月16日 星期四 19时07分04秒
// File Name     : 2750.cpp

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <time.h>

using namespace std;

const int MaxN=;

#define lc (po<<1)
#define rc ((po<<1)|1)
#define lson L,M,lc
#define rson M+1,R,rc

int LN[MaxN<<],RN[MaxN<<],BIT[MaxN<<],SUM[MaxN<<];
int ln[MaxN<<],rn[MaxN<<],bit[MaxN<<];
int minn[MaxN<<];

void pushUP(int po)
{
    SUM[po]=SUM[lc]+SUM[rc];

    minn[po]=min(minn[lc],minn[rc]);

    BIT[po]=max(BIT[lc],BIT[rc]);
    BIT[po]=max(BIT[po],max(SUM[lc]+LN[rc],SUM[rc]+RN[lc]));
    BIT[po]=max(BIT[po],LN[rc]+RN[lc]);

    LN[po]=max(LN[lc],SUM[lc]+LN[rc]);
    RN[po]=max(RN[rc],SUM[rc]+RN[lc]);

    bit[po]=min(bit[lc],bit[rc]);
    bit[po]=min(bit[po],min(SUM[lc]+ln[rc],SUM[rc]+rn[lc]));
    bit[po]=min(bit[po],ln[rc]+rn[lc]);

    ln[po]=min(ln[lc],SUM[lc]+ln[rc]);
    rn[po]=min(rn[rc],SUM[rc]+rn[lc]);
}

void update(int up,int ut,int L,int R,int po)
{
    if(L==R)
    {
        SUM[po]=BIT[po]=LN[po]=RN[po]=ut;
        bit[po]=ln[po]=rn[po]=ut;
        minn[po]=ut;
        return;
    }

    int M=(L+R)>>;

    if(up<=M)
        update(up,ut,lson);
    else
        update(up,ut,rson);

    pushUP(po);
}

int num[MaxN];

void build(int L,int R,int po)
{
    if(L==R)
    {
        LN[po]=RN[po]=BIT[po]=SUM[po]=num[L];
        ln[po]=rn[po]=bit[po]=num[L];
        minn[po]=num[L];
        return;
    }

    int M=(L+R)>>;

    build(lson);
    build(rson);

    pushUP(po);
}

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

    int N;
    int ans;

    scanf("%d",&N);

    for(int i=;i<=N;++i)
        scanf("%d",&num[i]);

    build(,N,);

    int M,a,b;

    scanf("%d",&M);

    while(M--)
    {
        scanf("%d %d",&a,&b);

        update(a,b,,N,);

        ans=max(BIT[],SUM[]-bit[]);

        if(ans==SUM[])
            ans-=minn[];

        printf("%d\n",ans);
    }

    return ;
}