HDU 5970 最大公约数

中文题

题意：

思路：

1、观察可得 模m的同余系和m的gcd都相同（这题多了一个c也是相同的）

2、由于取证所以不能用简单的用O(m^2)的做法，涉及到多1少1的

3、打表观察，例如i为模9为7的数 j为9

则i*j/f(i,j) 有这样的规律：

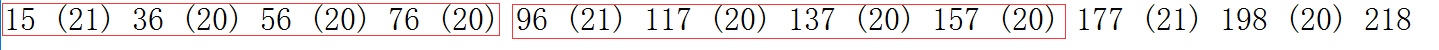
括号内为相邻值的差，而这个差是有循环节的，也就意味着，这可以看作4个等差数列。

又发现f(i,j)的c为4。

然后就大胆猜测c就是循环节。又试了几个数，果然是这样。

//不过很巧的是，循环节有一点小规律，但是没有仔细想，说不定可以有O(m^2)的做法

然后gcd的计算次数是log级别的，所以总的复杂度就是O(T*m^2*log(m))

//不过我的程序跑得不是很快。几乎是卡时间过的

具体细节看代码：

 LL f(int x, int y, int& g, int& c)
 {
     c = ;
     int t;
     while (y)
     {
         c++;
         t = x % y;
         x = y;
         y = t;
     }
     g = x;
     return x * x * c;
 }

 int n, m, p;
 void init()
 {
     get_int(n);
     get_int(m);
     get_int(p);
 }

 void solve()
 {
     int ans = , g, c;
     for (int j = ; j <= m; j++)
     {
         for (int i = ; i <= j && i <= n; i++)
         {
             LL ff = f(i, j, g, c);
             for (int k = ; k < c; k++)
             {
                 if (i + k * j > n) break;
                 LL a0 = (i + k * j) * j / ff;
                 LL d = c * j * j / ff;
                 LL num = (n - (i + k * j)) / (c * j) + ;
                 ans = ((ans + a0 * num) % p + num * (num - ) /  % p * d % p) % p;
             }
         }
     }
     printf("%d\n", ans);
 }

 int main()
 {
     int T;
     get_int(T);
     while (T--)
     {
         init();
         solve();
     }
     return ;
 }