关于FFT的硬件实现

---

DFT在实际应用中非常重要，可以计算信号的频谱，功率谱和线性卷积等。

离散傅里叶变换的公式：

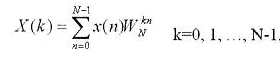
其中：

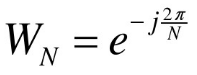 称为旋转因子。

由欧拉公式可得：

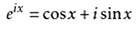
直接按DFT变换进行计算，当序列长度N很大时，计算量非常大，所需的时间非常长。

FFT是 快速傅里叶变换。其算法原理这里不再赘述，网上资料或者相关书籍的介绍很多。主要分为按时间抽取法和按频率抽取法。

这里介绍按时间抽取的基2算法的硬件实现。

下面介绍的部分需要了解蝶形运算是什么，这里不做分析。

先来看一张16点的蝶形运算图：

第1级（第1列）每个蝶形的两节点“距离”为1，第2级每个蝶形的两节点“距离”为2，第3级每个蝶形的两节点“距离”为4，第4级每个蝶形的两节点“距离”为8。由此推得，第m级蝶形运算，每个蝶形的两节点“距离”L=2^(m-1)。

对于16点的FFT，第1级有8组蝶形，每组有1个蝶形；第2级有4组蝶形，每组有2个蝶形；第3级有2组蝶形，每组有4个蝶形；第4级有1组蝶形，每组有8个蝶形。由此可推出，对于N点的FFT，第m级有N/2L组蝶形，每组有L=2^(m-1)个蝶形。

从上图我们可以分析出左边输入端与右边输出端的顺序关系，用二进制表示为：

左边                                                      右边

0000                                                     0000

1000                                                     0001

0100                                                     0010

1100                                                     0011

0010                                                     0100

1010                                                     0101

0110                                                     0110

1110                                                      0111

0001                                                     1000

·······                                                      ·······

不难看出，右边的逆序正是左边的正序，利用这一点，可以事先将输入序列重新排序。

关于旋转因子，可以事先计算出来 ，由于FPGA不擅长做浮点运算，需要将计算出的旋转因子扩大2^n倍。然后以.mif的格式存放在FPGA片上ROM中。

关于输入序列的长度N，最好是2的整数次幂。

为了提高速度，可将FFT的输入序列存放在FPGA片上RAM中，所以在使用FFT的项目中，选取FPGA芯片时，要考虑片上RAM的容量。

将片上RAM设置为TRUE DPRAM，两个口读，两个口写，提高存取效率，实际使用中自有妙用。

根据上图的蝶形运算图，可以大致确定 FFT的计算量。

直接的DFT算法运算量：

N*N ，单位为复数乘法的时间MT；

使用FFT算法的运算量：

N/2*log2(N)，单位为数乘法的时间MT；

算法运算量 比较：

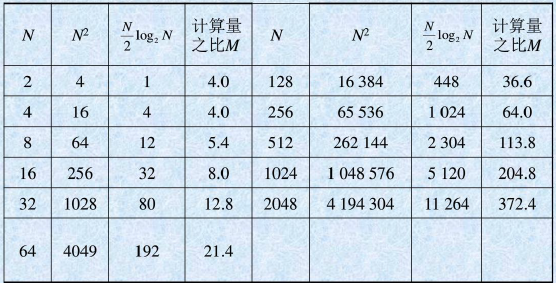
根据蝶形运算图，可以将FPGA设计层级结构分为3层：

蝶形级数循环层，

蝶形组数循环层，

蝶形个数循环层。

复数乘法可直接使用FPGA片内自带的乘法器，注意数据位宽，谨防溢出。

另外，被乘数和乘数必须为原码，做乘法时必须考虑数据的正负符号问题。

设计加法器和减法器时，由于存在符号问题，包括正数+正数，正数+负数，负数+负数，以及正数-正数，正数-负数，负数-正数，负数-负数，这些判断操作非常繁琐，设计时格外注意数据的大小及正负。

这里我们可以将设计变的简单：

将输入到加法器和减法器的两个数据先转换为补码，然后做加法运算，输出时再将补码转换成原码即可。

为了节省资源，尽可能使用移位代替乘法和除法。为了提高速度，可在适当的地方加入流水线操作。

关于精度问题：由于FPGA不擅长做浮点运算，必然存在精度问题。

首先，对存入ROM的旋转因子进行了放大，引入精度问题。

然后，在旋转因子的乘法中，引入精度问题。

再后续旋转因子的还原中，也引入精度问题。

提高精度，一方面在放大旋转因子时，可以适当提高放大倍数，另一方面，旋转因子还原中，尽量把还原除法放在最后输出的地方。

---

版权所有权归卿萃科技 杭州FPGA事业部，转载请注明出处

作者：杭州卿萃科技ALIFPGA

原文地址：杭州卿萃科技FPGA极客空间 微信公众号

---

扫描二维码关注杭州卿萃科技FPGA极客空间

---