[BJOI2017]魔法咒语 --- AC自动机 + 矩阵优化

bzoj 4860   LOJ2180   洛谷P3175

[BJOI2017]魔法咒语

题目描述：

Chandra 是一个魔法天才。

从一岁时接受火之教会洗礼之后，Chandra 就显示出对火元素无与伦比的亲和力，轻而易举地学会种种晦涩难解的法术。

这也多亏 Chandra 有着常人难以企及的语言天赋，让她能轻松流利地说出咒语中那些极其拗口的魔法词汇。

直到十四岁，开始学习威力强大的禁咒法术时，Chandra 才遇到了障碍。

根据火之魔法规则，禁咒的构成单位是 N 个基本词汇。

施法时只要凝聚精神力，说出一段用这些词语组成的长度恰好等于 L 的语言，就能释放威力超乎想象的火法术。

过去的魔法师们总结了几种表达起来最连贯的组合方式，方便施法者以最快语速完成法术。

但具有魔法和语言双重天才的 Chandra 不满足于这几种流传下来的禁咒，因为她可以毫无困难地说出普通人几乎不可能表达的禁咒语句。

然而，在实际施法时，Chandra 发现有些自创禁咒念出后不但没有预期效果，反而会使自己的精神力迅速枯竭，十分难受。

这个问题令 Chandra 万分不解。

她大量阅读典籍，到处走访魔法学者，并且不顾精神折磨一次又一次尝试新咒语，希望找出问题的答案。

很多年过去了，在一次远古遗迹探险中，Chandra 意外闯进了火之神艾利克斯的不知名神殿。

根据岩土特征分析，神殿应该有上万年的历史，这是极其罕见的。Chandra 小心

翼翼地四处探索，沿着魔力流动来到一间密室。她看见密室中央悬浮着一本书籍。

在魔法保护下书籍状况完好。精通上古语言的 Chandra 读过此书，终于解开了多年的困惑。

禁咒法术之所以威力强大，是因为咒语借用了火之神艾利克斯的神力。

这本书里记载了艾利克斯生平忌讳的 M 个词语，比如情敌的名字、讨厌的植物等等。

使用禁咒法术时，如果语言中含有任何忌讳词语，就会触怒神力而失效，施法者也一并遭受惩罚。

例如，若 ”banana” 是唯一的忌讳词语，“an”、”ban”、”analysis” 是基本词汇，

禁咒长度须是 11，则“bananalysis” 是无效法术，”analysisban”、”anbanbanban”是两个有效法术。

注意：一个基本词汇在禁咒法术中可以出现零次、一次或多次；

只要组成方式不同就认为是不同的禁咒法术，即使书写形式相同。

谜题破解，Chandra 心情大好。

她决定计算一共有多少种有效的禁咒法术。

由于答案可能很大，你只需要输出答案模 1,000,000,007 的结果。

输入格式：

第一行，三个正整数 N, M, L。

接下来 N 行，每行一个只含小写英文字母的字符串，表示一个基本词汇。

接下来 M 行，每行一个只含小写英文字母的字符串，表示一个忌讳词语。

输出格式

仅一行，一个整数，表示答案（模 \(10^{9}+7\)）。

数据范围：

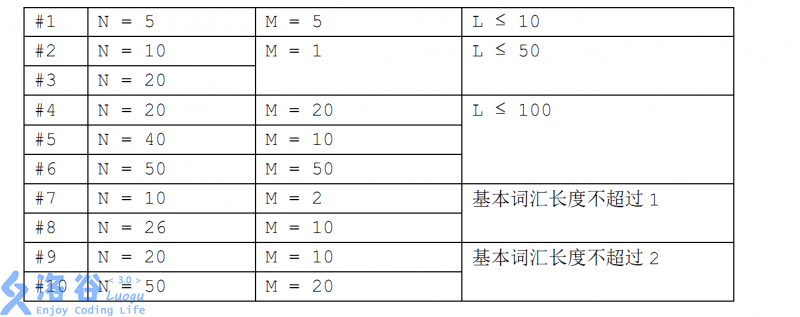
对于 100%的数据，1 ≤ N, M ≤ 50，1 ≤ L ≤ \(10^{8}\)，基本词汇的长度之和不超过100，忌讳词语的长度之和不超过 100。

保证基本词汇不重复，忌讳词语不重复。

AC自动机题感觉都是套路（3min秒掉好开心）

统计单词是不是？

先来个dp状态：\(dp(i,j)\)表示构造到第i位，再AC自动机上状态为j的方案数

AC自动机哪里来？

禁忌单词是不是？不能碰到是不是？AC自动机肯定就是你了。

限定单词？

好像不好处理，但是也没有什么。

原本常用dp：

\(dp(i,j)= \sum_{trans(v,c) = j} dp(i - 1,v)\)

稍微改一下：

\(dp(i,j) = \sum_{trans(v,words)}  dp(i - len(words),v) \)

words就是题面中给出的构成单词。

好像解决了？？？

并没有，对于60%的数据点，dp是可以解决的。

但是对于后面的点，L过大, 但是\(len(words)\)并不大，可以考虑矩阵优化

最后20分的点怎么办？？？

把状态抽象出来：

\(dp(i,...)= \sum dp(i-1,...) + \sum(dp(i-2,...) )\)

还是个线性递推式，依然可以用矩阵转移。

最终前60%数据的复杂度：O（\(L* n * \sum len(words) \)）

后40%数据的复杂度：O（\( \sum (2 * len(words))) ^ {3} *  \log L\)）

补充：

可以通过预处理来加速一部分。

本题需要一定的常数。

代码在此