「BZOJ 2534」 L - gap字符串

「BZOJ 2534」 L - gap字符串

题目描述

有一种形如 \(uv u\) 形式的字符串,其中 \(u\) 是非空字符串,且 \(v\) 的长度正好为 \(L\), 那么称这个字符串为 \(L-Gap\) 字符串 给出一个字符串 \(S\), 以及一个正整数 \(L\), 问 \(S\) 中有多少个 \(L-Gap\) 子串.

\(1 \leq |S| \leq 5 \times 10^4, L \leq 10\)

### 解题思路 :

考虑要对特征串计数，不妨枚举 单个 \(u\) 的长度 \(|u|\)，在串上设置 \(\left\lfloor \frac{|s|}{|u|}\right\rfloor\) 个关键点.

计算单个 \(u\) 覆盖某一关键点的所有串对应的 \(uvu\) 串的总数

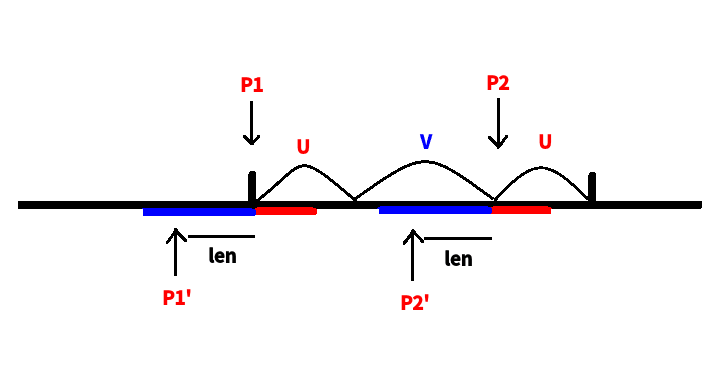
考虑当前有关键点 \(P_1\) 其对应的另外一个 \(u\) 所在的左端点点为 \(P_2\)

考虑 \(P_1, P_2\) 能作为 \(uvu\) 串中两个\(u\)的左端点的话，当且仅当 \(Lcp(P_1, P_2) \geq |u|\)

那么问题就转化为，所有覆盖关键点 \(P_1\) 的 \(u\) 串，与其对应点的 \(Lcp \geq |u|\) 的个数是多少

考虑覆盖 \(P_1\) 的 \(u\) 串的左端点为 \(P_1'\) ，\((P_1 - |u| < P_1' < P_1 + |u|)\)，其对应的另外一个\(u\) 的左端点为 \(P_2'\)

观察发现 \(P_1', P_2'\) 显然是由 \(P_1', P_2'\) 平移同一距离得到的

不妨求出后缀 \(P_1, P_2\) 的 \(Lcp\) 以及前缀 \(P_1, P_2\) 的 \(Lcs\)，也就是图中红色和蓝色的线段

显然 \(P_1', P_2'\) 移动到线段之外后不可能满足 \(Lcp(P_1', P_2') \geq |u|\)，所以答案就是线段上可行的 \(P_1'\) 数

也就是 \(\max(Lcp + Lcs - |u|, 0)\)

考虑这样做为什么是正确的

首先是时间复杂度，每次枚举一个 \(|u|\) ，对于 \(\left\lfloor \frac{|s|}{|u|}\right\rfloor\) 个关键点 \(O(1)\) 或 \(O(log|s|)\) 算 \(Lcs, Lcp\)

根据调和级数，复杂度是 \(O(|s|log|s|)\) 或 \(O(|s|log^2|s|)\)，足以通过此题

接下来分析算法的正确性，也就是为什么不会算重和算漏

考虑对于每一个长度为 \(|u|\) 的 \(u\) 串，当且仅当只能覆盖一个关键点，所以如果其有答案，必然会被关键点算到且被算一次

注意 \(Lcp\) 和 \(Lcs\) 要对 \(|u|\) 取模，不然算到的答案就不是覆盖当且关键点的答案，会因为算法写挂了而算重

这里我用了二分 + \(hash\) 求 \(Lcs, Lcp\) ，是两个 \(log\) 的，实际上如果用 \(Sa\) 的话，复杂度就如上述一样，省去一个 \(log\)

/*program by mangoyang*/
#include<bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define N (100005)
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
const ull base = 233;
char s[N];
int n, m, ans;
ull pw[N], hs[N];
inline ull get(int l, int r){
    if(l > r) return 0; return hs[r] - hs[l-1] * pw[r-l+1];
}
inline int getpre(int x, int y, int lim){
    int l = 0, r = lim, ans = 0;
    while(l <= r){
        int mid = l + r >> 1;
        if(get(x - mid + 1, x) == get(y - mid + 1, y))
            ans = mid, l = mid + 1; else r = mid - 1;
    }
    return ans;
}
inline int getsuf(int x, int y, int lim){
    int l = 0, r = lim, ans = 0;
    while(l <= r){
        int mid = l + r >> 1;
        if(get(x, x + mid - 1) == get(y, y + mid - 1))
            ans = mid, l = mid + 1; else r = mid - 1;
    }
    return ans;
}
inline void solve(int L, int R){
    int len = (R - L + 1 - m) / 2, l1 = L, l2 = R - len + 1;
    int llen = getpre(l1, l2, len), rlen = getsuf(l1, l2, len);
    int now = (llen && rlen) ? llen + rlen - 1 : llen + rlen;
    if(now >= len) ans += now - len + 1;
}
int main(){
    pw[0] = 1, scanf("%d", &m);
    scanf("%s", s + 1); int n = strlen(s + 1);
    for(int i = 1; i < N; i++) pw[i] = pw[i-1] * base;
    for(int i = 1; i <= n; i++) hs[i] = hs[i-1] * base + s[i];
    for(int k = 1; k <= (n - m) / 2; k++)
        for(int i = 1; i <= n; i += k) solve(i, i + 2 * k + m - 1);
    cout << ans;
    return 0;
}