PCA 学习笔记

先简单记下，等有时间再整理

PCA 主要思想，把 协方差矩阵 对角化，协方差矩阵是实对称的。
里面涉及到矩阵论的一点基础知识：

基变换：

Base2 = P · Base1

相应的 坐标变换

P · coordinate2 = coordinate1

将 X 转换到 Y，Y = P · X  , X是原来的基，Y是新的基，P是过渡矩阵。

后面可以用 实对称阵的相似对角化来处理。

D = Y · Y^T = P(1/m·X·X^T)P^T

讲的有点乱

直接上代码 和图吧。

# -*- coding=utf-8 -*-

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

'''
    PCA is similar diagnalization Covariance Matrix
'''

X = pd.read_csv('testSet.txt',header=None,delimiter='\t').as_matrix()
# print(X)

# 1.0centralization
# print(X.mean(axis=0))     [9.0639,9.096]
X_cen = X - X.mean(axis=0)
# 2.0 covariance matrix
cov_X =  np.dot(X_cen.T,X_cen) / X_cen.shape[0]
# 3.0 get eigVector which is p  A = pXX^Tp^T
# Y = p
eigVal,eigVector = np.linalg.eig(cov_X)
P = eigVector[:,::-1]
# P[:,-1] = np.array([0,0])
# Y = np.dot(P,(X_cen.T)).T
print(P)
P = np.linalg.inv(P)
'''
[-0.52045195 -0.85389096]
 [-0.85389096  0.52045195]]
'''

cor = np.linspace(-2,2,1000)
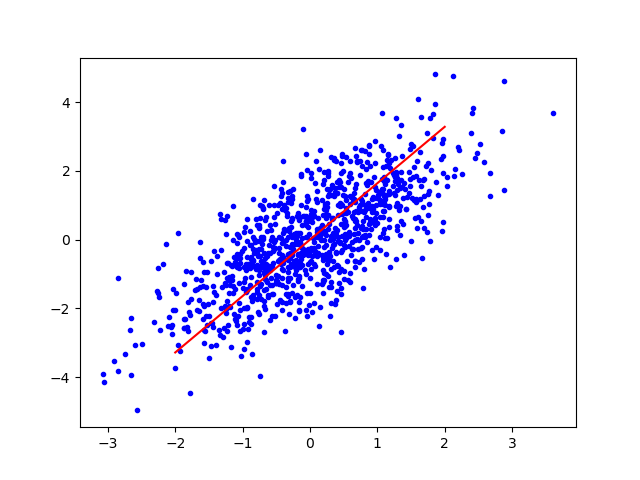
plt.plot(X_cen[:,0],X_cen[:,1],'.b')
plt.plot(cor,cor*P[0,1]/P[0,0],'-r')
# plt.plot(Y[:,0],Y[:,1],'.r')
plt.show()

　　

参考:
https://www.cnblogs.com/mikewolf2002/p/3429711.html