STREAMING #5 题解 3.高位网络

高维网络

【题目描述】 
现在有一个 d 维的坐标网格，其中第 i 维坐标的范围是[0,a_i]。在这个范围内建立一个有向图：我们把范围内的每个整点（每一维坐标均为整数的点）当做图上的顶点。设点 A(0,0,⋯,0),B(a_1,a_2,⋯,a_d)。对于范围内的点(x_1,x_2,⋯,x_d)，它会向以下这些点（如果目标点在范围内）连有向边：(x_1+1,x_2,⋯,x_d),(x_1,x_2+1,⋯,x_d),⋯,(x_1,x_2,⋯,x_d+1) 
现在从点 A 到点 B 会有若干条路径，路径的条数可以十分简单地算出。然而不幸的是，范围内有 p 个点被破坏了（点 A 和点 B 不会被破坏） ，其中第 i个点的坐标为(x_(i,1),x_(i,2),⋯,x_(i,d))。你需要算出从点 A 到点B 剩余的路径条数。 
由于答案可能很大，你只需要输出它对 1,000,000,007 取模的结果。 
【输入格式】 
第一行为两个整数 d，p。 
第二行为 d 个整数，其中第 i 个数是 a_i。 
接下来 p 行，每行 d 个整数，其中第 i 行第 j 个数是 x_(i,j)。 
【输出格式】 
一个整数，表示从点 A 到点 B 剩余的路径条数对 1,000,000,007 取模的结果。 
【输入样例】 
2 1 
2 1 
1 0 
【输出样例】 
1 
【数据范围】 

30分算法
• 在前30分当中，数据规模非常小，可以暴搜每条路线。

d=1的算法
• 对于d=1的情况，如果没有点被破坏则答案是1，否则答案是0。

p=0的算法

•运用排列组合公式：二维：C(n,n+m)；

多维：

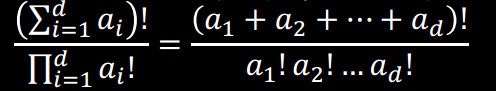
阶乘可以暴力算，注意除法要用逆元（费马小定理求逆元）算。

【题解】【dp+组合数+容斥原理】 
【f[i]表示从A到i不经过被破坏的点的路径条数；g[i][j]表示从i到j可以经过的被破坏的点的方案数（可以用组合数求）】 
【g[i][j]：（各维度权值之和的阶乘）/（各维度阶乘之积），如二维情况：（行数+列数）！/（行数！×列数！）】 
【f[i]＝总路径条数－不合法，f[x]=g[A][x]-Σf[y]*g[y][x]】 
【最后输出f[B]】

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #define man 10000010
 #define sc(x) scanf("%d",&x)
 #define ll long long
 #define mod 1000000007
 using namespace std;
 struct node
 {
     int x[];
     }a[];//每个点的坐标
 ll mi[man],sum[],f[],g[][],h[];
 /*
     mi[]:求i的阶乘；
     sum[]:每个点的坐标和（为了之后的p=0做准备）；
     f[]:从A到i不经过被破坏的点的路径条数；
     g[][]:从i到j可以经过的被破坏的点的方案数（可以用组合数求）;
     h[]:每两个点坐标之间的差值；
     */
 int d,p;
 int cmp(node a,node b)
 {
     for(int i=;i<=d;i++)
     {
         if(a.x[i]<b.x[i])return ;
         if(a.x[i]>b.x[i])return ;
         }
     }
 //    cmp：从一维开始从小到大排序；
 inline void pow1()
 {    mi[]=;
     for(ll i=;i<=;i++)
         mi[i]=(mi[i-]*i)%mod;
     }
 //pow1:计算阶乘；
 ll bpow(int a,int b)
 {
     ll ans=,base=a;
     while(b)
     {
         if(b&) ans=ans*base%mod;
         base=base*base%mod;
         b>>=;
         }
     return ans;
     }
 //快速幂；
 inline void solve()
 {
     for(int i=;i<=p;i++)
     {
         ll t=mi[sum[i]];
         ll t1=;
         for(int j=;j<=d;j++)
             if(a[i].x[j])
                 t1=(t1*mi[a[i].x[j]])%mod;
         ll ans=bpow(t1,mod-);
         g[][i]=t*ans%mod;
         }//运用费马小定理计算从A点至各点的路径总数；
     for(int i=;i<=p;i++)
         for(int j=;j<=p;j++)
         {
             ll tot=;bool b=;
             for(int k=;k<=d;k++)
             {
                 h[k]=a[j].x[k]-a[i].x[k];
                 tot+=h[k];
                 if(h[k]<) //因为是单向边（从i至j）,所以j-i的坐标差>=0;
                 {
                     b=;
                     break;
                     }
                 }
                 if(!b) continue;
                 ll t=mi[tot];
                 ll t1=;
                 for(int k=;k<=d;k++)
                     if(h[k]) t1=(t1*mi[h[k]])%mod;
                 ll ans=bpow(t1,mod-);
                 g[i][j]=t*ans%mod;
             }//运用费马小定理求两点之间路径总数；
     return ;
     }

 int main()
 {    freopen("cube.in","r",stdin);
     freopen("cube.out","w",stdout);
     sc(d);sc(p);
     p++;
     for(int i=;i<=d;i++)
         sc(a[p].x[i]);//每维极值相当于B点（终点）坐标；
     for(int i=;i<=p-;i++)
         for(int j=;j<=d;j++)
             sc(a[i].x[j]);
     sort(a+,a++p,cmp);
     for(int i=;i<=p;i++)
         for(int j=;j<=d;j++)
         {sum[i]+=a[i].x[j];sum[i]%=mod;}
     pow1();
     solve();//预处理g[i][j];
     for(int i=;i<=p;i++)
     {
         f[i]=g[][i]%mod;
         for(int j=;j<i;j++)
             f[i]=(f[i]-f[j]*g[j][i])%mod;
         f[i]=(f[i]%mod+mod)%mod;
         }
     cout<<f[p]<<endl;
     return ;
     }

费马小定理：a/b mod p ==a* b^p-2 mod p;

证明略。