NB二人组(一)----堆排序
堆排序前传--树与二叉树简介
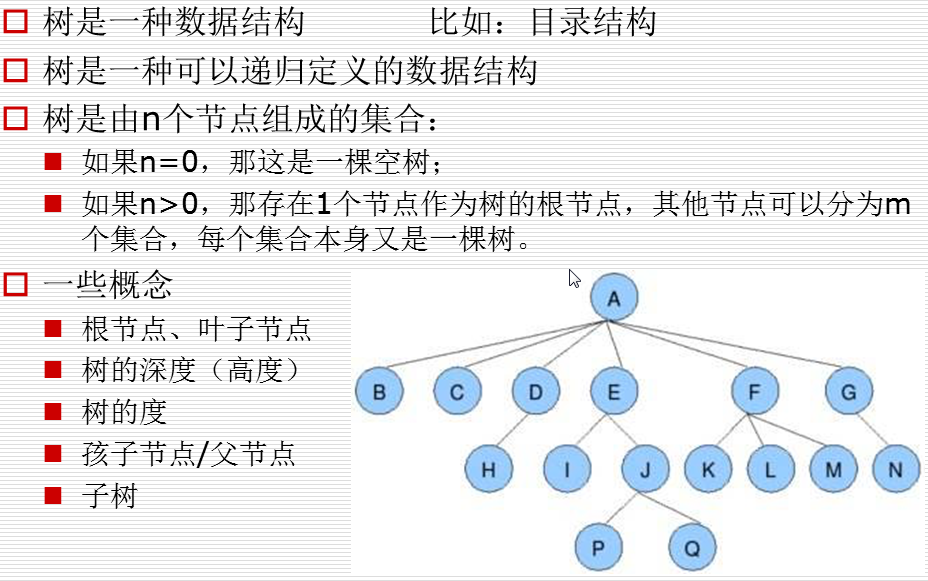
特殊且常用的树--二叉树

两种特殊的二叉树

二叉树的存储方式

二叉树小结

堆排序

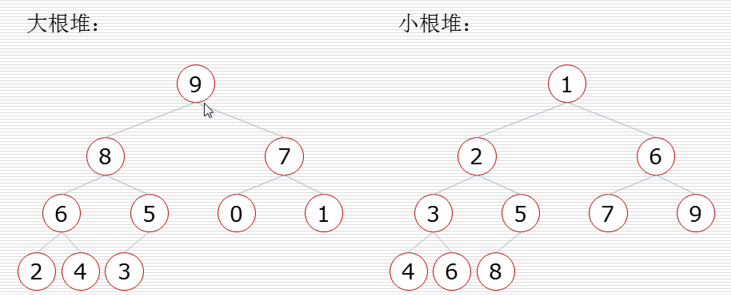
堆这个玩意.......

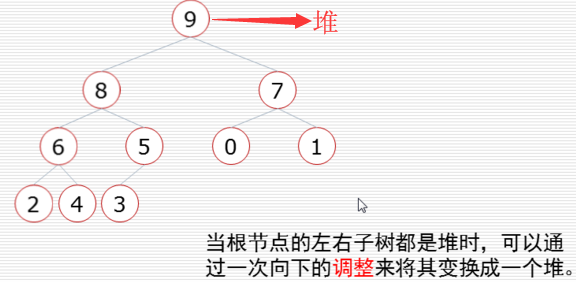
堆排序过程:

构造堆:
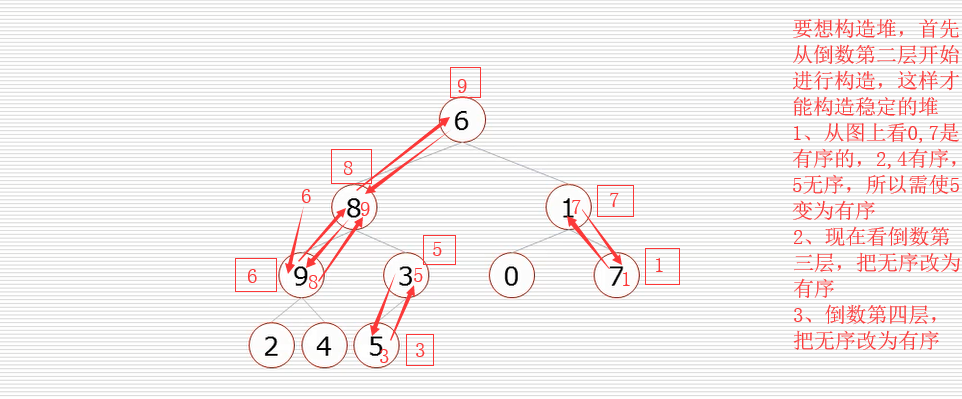
堆排序的算法程序(程序需配合着下图理解):
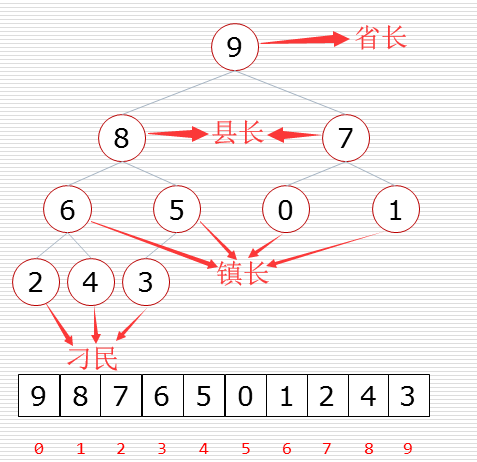
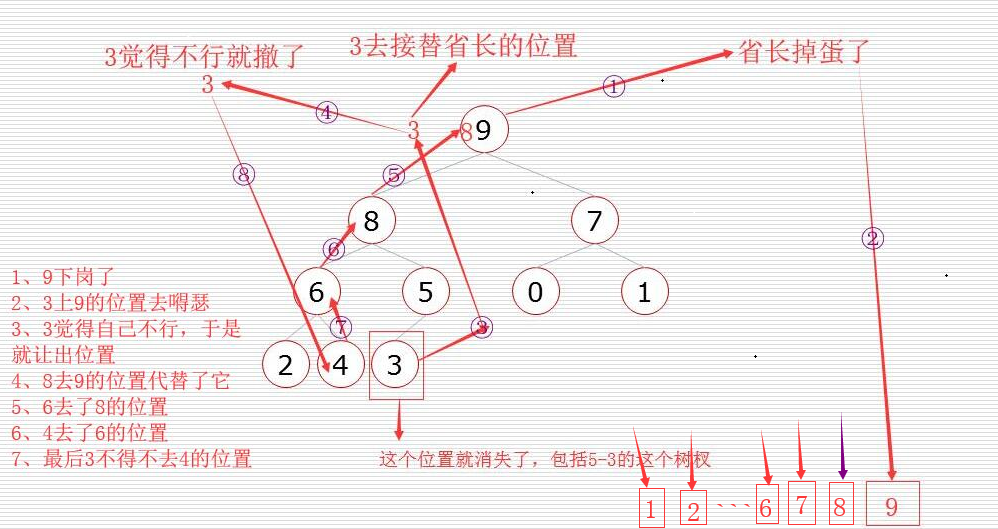
def sift(data,low,high): # 调整函数
i = low # 树的根 也就是父亲 ,这里只领导
j = 2 * i + 1 # 根的左孩子 也就是 儿子 ,这里指小领导
tmp = data[i] # 把根 取出来 做调整 , 在这里 领导
while j <= high: # high其实就是 根的右儿子(也就是最后一个儿子),如果 j= high 则表示没有右儿子,也就是说这里必须有儿子在
if j < high and data[j] < data[j + 1]: # j < high 代表有右儿子 , data[j] < data[j + 1] 说明右儿子比左儿子大
j += 1 # 这个 j 则变为右儿子 ,也就是 若有比 j 大的值,则 j 就变为比他大的那个值
if tmp < data[j]: # 如果领导不能干
data[i] = data[j] # 则小领导上位
i = j # 小领导变为大领导
j = 2 * i + 1 # 小小领导变为小领导
else: # 如果领导能干
break # 那就待着吧
data[i] = tmp # 到最后 i 这里肯定会有空位 ,所以无论 tem 是谁 都要占住这个空位 # 方法一
def heap_sort(data): # 开始进行堆排序
n = len(data) # n 为长度
# 开始建堆
for i in range(n // 2 - 1,-1,-1): # n//2-1为图片中的 5 的位置,-1 为到0 结束 ,-1 为步长
sift(data,i,n-1) # i 为low也就是其父节点,n-1 为high 也就是堆的最后 ,也就是每次调整小领导所在的堆
# 堆建好了
# 升序排列
for i in range(n-1,-1,-1): # n-1为high 也就是从堆得最后 一直到 0为止,也就是从刁民到领导
data[0],data[i]=data[i],data[0] # 堆的顶部 和 堆的末尾 互换, 也就是领导退休,刁民上位
sift(data,0,i-1) # 0 代表着领导 ,i-1 代表着这个堆的位置不能把领导算在内了,也就是领导退休了,把他赶出这个城市了
# 降序排列,耗内存 # 方法二 耗内存
# def heap_sort(data): # 开始进行堆排序
# n = len(data) # n 为长度
# # 开始建堆
# for i in range(n // 2 - 1, -1, -1): # n//2-1为图片中的 5 的位置,-1 为到0 结束 ,-1 为步长
# sift(data, i, n - 1) # i 为low也就是其父节点,n-1 为high 也就是堆的最后 ,也就是每次调整小领导所在的堆
# # 堆建好了
# # 降序排列
# li=[] # 监狱
# for i in range(n-1,-1,-1):
# li.append(data[0]) # 领导进监狱了
# data[i] = data[0] # 领导下位了
# sift(data,0,i-1) # 领导离开了城市 , 进监狱了
堆的应用


☆☆☆☆堆模块库地址(点击这行字)☆☆☆☆

利用堆模块来进行演算
import heapq # 堆模块
heap = []
data = list(range(10000))
random.shuffle(data)
for i in data:
heapq.heappush(heap,i)
for i in range(len(heap)):
print(heapq.heappop(heap)) print(heapq.nlargest(10,data)) # 堆模块 从大到小 排序 只取前十个数
print(heapq.nsmallest(10,data)) # 堆模块 从小到大 排序 只取前十个数
程序演示:
`
`
`
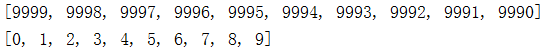
NB二人组(一)----堆排序的更多相关文章
- 算法 排序NB二人组 堆排序 归并排序
参考博客:基于python的七种经典排序算法 常用排序算法总结(一) 序前传 - 树与二叉树 树是一种很常见的非线性的数据结构,称为树形结构,简称树.所谓数据结构就是一组数据的集合连同它们的储 ...
- low逼三人组、nb二人组、归并、希尔排序----小结
- NB二人组(二)----归并排序
归并排序的思路: 归并算法程序(配合下图进行思考): def merge(li,low,mid,high): i = low j = mid + 1 ltmp=[] while i <= mid ...
- 列表排序之NB三人组附加一个希尔排序
NB三人组之 快速排序 def partition(li, left, right): tmp = li[left] while left < right: while left < ri ...
- 排序NB三人组
排序NB三人组 快速排序,堆排序,归并排序 1.快速排序 方法其实很简单:分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”.先从右往左找一个小于6的数,再从左往 ...
- 算法排序-NB三人组
快速排序: 堆排序: 二叉树: 两种特殊二叉树: 二叉树的存储方式: 小结: 堆排序正题: 向下调整: 堆排序过程: 堆排序-内置模块: 扩展问题topk: 归并排序: 怎么使用: NB三人组小结
- 排序算法之NB三人组
快速排序 思路: 例如:一个列表[5,7,4,6,3,1,2,9,8], 1.首先取第一个元素5,以某种方式使元素5归位,此时列表被分为两个部分,左边的部分都比5小,右边的部分都比5大,这时列表变成了 ...
- Binary Heap(二叉堆) - 堆排序
这篇的主题主要是Heapsort(堆排序),下一篇ADT数据结构随笔再谈谈 - 优先队列(堆). 首先,我们先来了解一点与堆相关的东西.堆可以实现优先队列(Priority Queue),看到队列,我 ...
- 牛B三人组-快速排序-堆排序-归并排序
快速排序 随便取个数,作为标志值,这里就默认为索引位置为0的值 记录左索引和右索引,从右往左找比标志值小的,小值和左索引值交换,右索引变化,然后从左往右找比标志值大的,大值和右索引值交换,左索引变化 ...
随机推荐
- PAT 甲级 1132 Cut Integer
https://pintia.cn/problem-sets/994805342720868352/problems/994805347145859072 Cutting an integer mea ...
- Hive查看执行日志
HIVE-如何查看执行日志 HIVE既然是运行在hadoop上,最后又被翻译为MapReduce程序,通过yarn来执行.所以我们如果想解决HIVE中出现的错误,需要分成几个过程 HIVE自身翻译成为 ...
- sublime插件时间
import datetime import sublime_plugin class AddCurrentTimeCommand(sublime_plugin.TextCommand): def r ...
- UserAgent 设置 php 抓取网页
转载:http://www.webkaka.com/tutorial/php/2013/111846/ hp抓取网页,可谓轻而易举,几行代码就可以搞定.不过,如果你有所疏忽,程序写得不够严密,就会出现 ...
- Spring Cloud Sleuth服务跟踪
监控 使用zipkin(https://zipkin.io/) 监控服务构建: (普通的springBoot项目) <!--引入的zipkinServer依赖--> <depende ...
- bzoj4184shallot
题意 给出一个初始为空的数字集合,每次添加一个数字/删除一个存在的数字,然后输出选出一些数进行异或能够得到的最大数值.操作次数<=500000,数字大小<2^31 分析 看上去我们只要写一 ...
- day06 小数据池和编码
一. 上次课内容回顾字典:由{}括起来. 每个元素用逗号隔开, key:value的形式存储数据key: 不可变的. 可哈希的.增删改查:1. 增加: 直接用新key来赋值. dict[key] = ...
- Python常忘的进阶知识(下)
0.目录 1.装饰器 1.1 为每个函数都增加一个功能 1.2 装饰器只是一种模式 1.3 语法糖 1.4 函数需要传递参数,该如何更改装饰器? 1.5 函数需要传递关键字参数,该如何更改装饰器? 2 ...
- 【WebAPI】新手入门WebAPI
一.前言 工作也有一年多了,从进入公司就一直进行BIM(建筑信息模型)C/S产品的研发,平时写的最多的就是Dev WPF.一个偶然的时机,产品需要做支付宝扫码与微信扫码,所以需要了解产品服 ...
- 【BZOJ2878】【NOI2012】迷失游乐园(动态规划)
[BZOJ2878][NOI2012]迷失游乐园(动态规划) 题面 BZOJ 题解 记得以前考试的时候做过这道题目 这题的暴力还是非常显然的,每次\(dfs\)一下就好了. 时间复杂度\(O(n^2) ...
