浅谈卡特兰数(Catalan number)的原理和相关应用

一、卡特兰数(Catalan number)

1.定义

组合数学中一个常出现在各种计数问题中出现的数列(用c表示)。以比利时的数学家欧仁·查理·卡特兰的名字来命名；

2.计算公式

(1)递推公式

c[n]=Σ(0≤k<n)c[k]c[n-k-1]，边界条件为c[0]=1;

其递推解为c[n]=C(2n,n)/(n+1)，即卡特兰数的通项公式，其中C表示数的组合；

根据组合公式我们可以化简得c[n]=2n(2n-1).....(n+2)/n!;

(2)另类递推式

c[n]=c[n-1](4n-2)/(n+1)，边界条件为c[0]=1;

其递推解为c[n]=C(2n,n)-C(2n,n-1),C表示数的组合；

(3)其他公式

c[n]=(Σ(0≤i≤n)C(i,n)^2)/(n+1);

ps：通过展开可以发现它们的本质是一样的；

3.简单应用

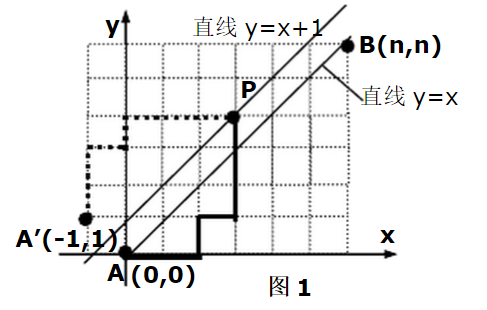
(1)求解路径方案数：如图所示，从原点(0,0)到点B(n,n)，只能向右或向上进行长度为一个单位的移动，路线一直处于y=x之下（不越过直线y=x）的不同路径方案数；

Solution：每个n的解都可以看做先前的解数（再向右向上即为所求）加上不触及各个y=x上的点到达B点的方案数，可以发现其递推公式即为卡特兰数计算公式；

(2)求01串的个数：n个0与n个1构成的序列方案数，使得任何一个前缀0的个数不少于1的个数；

Solution：将0看做在坐标系中向右走一步，1看做向上走一步，则问题可化简为从原点到(n,n)所有路线中一直处于y=x之下（不越过直线y=x）的不同路径方案数，与上题相同，方案数即为对应n的卡特兰数；

(3)给定节点求解二叉树的个数：已知由n个节点，求形成不同的二叉树有多少种？

Solution：将向左生成子树看做0，向右生成字数看成1，则问题化简为求n/2个0和n/2个1构成数串的不同方案数，即上题无条件解的一半，与上题答案相同，形成不同的树的个数即为对应n的卡特兰数；

(4)求凸边形进行三角剖分的不同方案数：在一个有n+3条边的凸多边形中，求通过若干条互不相交的对角线，把这个多边形划分成若干个三角形的不同方案数。

Solution：因为每一条边都一定是剖分后的三角形的一条边，任意一条边都会把多边形分成两个小多边形，那么根据乘法原理，解即为划分成不同多边形的方案数对应小多边形的划分方案数之和，即f[n]=Σ(3≤k≤n-3)f[k]f[n-k-1]，可以发现解数即为n对应的卡特兰数；

(5)n对括号正确匹配数目:给定n对括号，求括号正确配对的字符串数;

Solution：因为是匹配问题，那么最后一个左括号必然有唯一右括号与其匹配，假设f[n]为n对括号的正确配对数目，那么有递推关系f[n]=f[0]f[n-1]+f[1]f[n-2]+...+f[n-1]f[0]，显然f[n]是n对应的卡特兰数。

4.卡特兰数的扩展（折线原理）

对于在n位的2进制中，有m个0，其余为1的catalan数为：C(n,m)-C(n,m-1)。其可由应用(1)证明；

二、相关应用

1.[NOIP2003]栈

题解随笔：http://www.cnblogs.com/COLIN-LIGHTNING/p/8481413.html

2.[洛谷P1722]矩阵II

Description

给定一个长度为2n的数列，现让你自由地放入红色算筹和黑色算筹，求对于所有的i(1<=i<=2n)，使第1~i格中红色算筹个数大于等于黑色算筹的方案数；

输入：n

输出：对100取模后的方案数；

Solution

1.将红看做入栈操作，黑看为出栈操作，问题即为求不同的合法的入栈出栈序个数；

2.那么解法与上题相同，易得解即为对应的卡特兰数；

3.我们可以考虑用递推式(1)求卡特兰数，取模更容易；

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstring>

#include<algorithm>

using namespace std;

int main(){

	unsigned long long ctl[110],i,j,k,n;

	memset(ctl,0,sizeof(ctl));

	ctl[0]=ctl[1]=1;

	ctl[2]=2;

	scanf("%d",&n);

	for(i=3;i<=n;++i)

		for(j=0;j<i;++j){

			ctl[i]+=ctl[j]*ctl[i-j-1];

			ctl[i]%=100;

		}

	printf("%d\n",ctl[n]);

	return 0;

}

3.[洛谷P1976]鸡蛋饼

Description

最近小 x 又发现了一个关于圆的有趣的问题：在圆上有2N 个不同的点，小 x 想用 N 条线段把这些点连接起来（每个点只能连一条线段），使所有的线段都不想交，他想知道这样的连接方案有多少种？

输入输出格式

输入格式：有且仅有一个正整数 N

输出格式：要求的方案数（结果 mod 100000007）。

Solution

1.可将问题化简为求n+3边形进行三角剖分的方案数，解法就显而易见了；

2.对1e8+7取模可以考虑使用递推公式（1）解决；

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstring>

#include<algorithm>

using namespace std;

int main(){

	unsigned long long ctl[32768],i,j,k,n;

	memset(ctl,0,sizeof(ctl));

	ctl[0]=ctl[1]=1;

	ctl[2]=2;

	scanf("%d",&n);

	for(i=3;i<=n;++i)

		for(j=0;j<i;++j){

			ctl[i]+=ctl[j]*ctl[i-j-1];

			ctl[i]%=100000007;

		}

	printf("%d\n",ctl[n]);

	return 0;

}

4.[AHOI2012]树屋阶梯

题解随笔：http://www.cnblogs.com/COLIN-LIGHTNING/p/8481432.html

5.[HNOI2009]有趣的数列

题解随笔：http://www.cnblogs.com/COLIN-LIGHTNING/p/8481448.html

6.[SCOI2010]生成字符串（卡特兰数的扩展）

题解随笔：http://www.cnblogs.com/COLIN-LIGHTNING/p/8481454.html